 |
Правила перевода из одной системы счисления в другую.
|
|
|
|
Любое число N в позиционной системе счисления с основанием p может быть представлено в виде полинома от основания p:
N = anpn+an-1pn-1+... +a1p+a0+a-1p-1+a-2p-2+...
здесь N - число, aj - коэффициенты (цифры числа), p - основание системы счисления (p>1).
Принято представлять числа в виде последовательности цифр:
N = anan-1... a1a0. a-1a-2...
В этой последовательности точка отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях). Точка опускается, если нет отрицательных степеней (число целое).
Чем меньше основание системы счисления, тем больше разрядов требуется для записи того же числа. Наиболее громоздкой получается запись в системе с наименьшим возможным основанием -- двоичной. Но то, что удобно для компьютера, оказывается очень неудобным для человека. Можно было бы переводить их в десятеричную систему и обратно... Однако, этот перевод довольно трудоемкий. И вот какой нашли выход. Если взять две системы счисления, такие что основание одной будет степенью основания другой (их иногда называют родственными), перевод будет делаться очень быстро.
Перевод из десятичной в произвольную позиционную систему счисления.
Для перевода из десятичной в произвольную позиционную систему счисления необходимо делить число с остатком на основание системы счисления до тех пор, пока частное больше основания системы счисления.
Рассмотрим на примере преобразования чисел из десятичной системы счисления в двоичную.
Метод 1.
Деление на 2 в убывающей степени. Можно преобразовать десятичное число в двоичное, производя деление десятичного числа на 2 в соответствующей степени. Предположим, необходимо получить двоичный эквивалент десятичного числа 76. Наибольшим числом, которое не превышает 76 и которое можно выразить как два в степени, является число 64 (26). Поэтому необходимо установить бит 6 в двоичном эквиваленте:
|
|
|
01000000 = 64
Вычтем 64 из 76 и получим число 12. Наиболее близкое к нему число, выраженное как 2 в стпени, будет 8 (23), поэтому устанавливаем бит 3:
+8
01001000 ß 72
Вычтем 8 из 12 и получим число 4, которое можно выразить как 22. Устанавливаем бит 2. Так как остатка больше нет, то получаем окончательное двоичное число 01001100b. Таким образом, был получен двоичный эквивалент путем последовательного вычитания чисел, выраженных как 2 в степени.
Последовательность шагов показана ниже:
72/64 = 1, остаток 12
12/8 = 1, остаток 4
4/4 = 1, остаток 0
Как только остаток станет равным нулю, цикл останавливается. Такой способ можно использовать при ручном преобразовании чисел.
Метод 2.
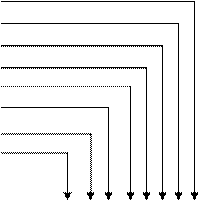
Повторяющееся деление на 2. Другой путь преобразования десятичного числа в двоичное, это последовательное деление десятичного числа на 2. Остаток от деления на каждом шаге будет заполнять соответствующие разряды двоичного числа. Для демонстрации метода возьмем ранее использованное число 76 (рис.1).
76 / 2 = 38, остаток 0
38 / 2 = 19, остаток 0
19 / 2 = 9, остаток 1
9 / 2 = 4, остаток 1
4 / 2 = 2, остаток 0
2 / 2 = 1, остаток 0
1 / 2 = 0, остаток 1
0 / 2 = 0, остаток 0
0 1 0 0 1 1 0 0
Рис 1. Преобразование чисел
На рисунке видно, что деление производилось восемь раз. Первый остаток был помещен в нулевой разряд. Этот метод можно считать идеальным для создания циклического алгоритма, но он отнимает много времени при вычислении вручную.
Рассмотрим еще одну модификацию этого метода.
Пример.
Перевести десятичное число в двоичное 23.12510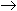 
"2" с.с.
| 1) Переведем целую часть: | 2) Переведем дробную часть: |
| 
|
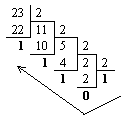
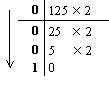
Таким образом: 2310 = 101112; 0.12510 = 0.0012.
Результат: 23.12510 = 10111.0012.
|
|
|
Необходимо отметить, что целые числа остаются целыми, а правильные дроби - дробями в любой системе счисления.
Таким же образом поступаем для перевода в 16-ричную систему счисления.
Перевести 62210 "16" с.с.
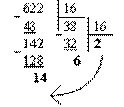
Результат: 62210 = 26E16
|
|
|
