 |
Перевод произвольной позиционной системы счисления в десятичную.
|
|
|
|
Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
Рассмотрим пример перевода двоичного числа 101100,0112 в десятичное.
1011002 =
= 1 · 25 + 0 · 24 + 1 · 23 + 1 · 22 + 0 · 21 + 0 · 1 =
= 1 · 32 + 0 · 16 + 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 =
= 32 + 8 + 4 + 0 = 4410
Целая часть этого числа равна 44, а вот перевод дробной части:
Итак, число 1100,0112 = 12,37510.
Для удобства перевода, целую и дробную части числа почти всегда переводят по-отдельности, а результат потом суммируют.
Точно также осуществляется перевод из любой системы счисления, только вместо «2» ставится основание системы.
Перевести 1216,04(8).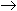 
"10" с.с.
1216,04(8)=1×83+2×82+1×81+6×80+4× 8-2 = 512+128+8+6+0,0625 = 654,0625(10).
Перевести 29A,5(16).. 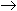"10" с.с.
29A,5(16) = 2×162+9×161+10×160+5×16-1 = 512+144+10+0,3125 = 656,3125(10).
Перевод из двоичной в шестнадцатеричную системы
Для этого типа операций существует упрощенный алгоритм.
Д ля шестнадцатеричной — разбиваем на квартеты, преобразуем по таблице.
В таблице показано соответствие двоичных чисел шестнадцатеричным цифрам. Большое двоичное число можно легко выразить с помощью шестнадцатеричных цифр.
Таблица 4.
| Двоичное | Шестнадцетеричное | Двоичное | Шестнадцетеричное |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Например, двоичное число 10101011100101111000011011100101 может быть легко представлено шестнадцатеричным значением АВ9786Е5:
| А | В | Е | |||||
Пример:
0010 1001 1010→ 29A(16)
Перевод из шестнадцатеричной системы счисления в двоичную.
|
|
|
Для этого типа операций существует упрощенный алгоритм-перевёртыш.
Преобразуем цифры шестнадцатеричного числа по Таблице 4 в квартеты.
Пример:
29A(16) → 0010 1001 1010
Числа со знаком.
Двоичные числа могут быть как со знаком (signed), так и без знака (unsigned). Числа без знака используют все восемь битов для получения значения. Например, 11111111 = 255. Просуммировав значения всех битов, получим максимально возможное значение, которое может хранить байт без знака (255). Для слова без знака это значение будет составлять 65 535. Байт со знаком использует только 7 битов для получения значения, а старший восьмой бит зарезервирован для знака, при этом 0 соответствует положительному значению, а 1 – отрицательному. На представленном ниже рисунке 1.4 показано отображение положительного и отрицательного числа 10. 
Знаковый бит
   1
|
  0
|
Рис.2 Отображение положительногои отрицательного числа 10.
Дополнение до двух.
Чтобы не усложнять процессор, отдельный блок для реализации операции вычитания не делают, эту операцию выполняет блок суммирования. Но перед суммированием отрицательные числа преобразовываются в дополнительное число. Это такое число, которое в сумме с исходным числом дает 0. Например, десятичное –6 будет дополнительным для 6, так как 6 + 6 = 0. Таким образом, вместо операции вычитания А-В процессор суммирует с положительным числом А дополнительное к В: А + (-В). Вместо того, чтобы вычесть 4 из 6, процессор просто складывает -4 и 6.
6 + - 4 = 2
Когда производится работа с двоичными числами, для дополнительного числа используется термин дополнение до двух (two’s complement). Также встречается такое определение, как двоичное дополнение. Например, для двоичного значения 0001 двоичным дополнением до двух будет 1111. Такое число получается из исходного числа после изменения всех единиц на нули, а нулей на единицы и прибавлением к получившемуся числу единицы:
|
|
|
N: 0001
Инвертированное N: 1110
Добавить 1: 1111
Если сложить N и дополнение до двух к N, то получим 0: 0001 + 1111 = 0000. Операция получения дополнения до двух полностью обратима. Например, для отрицательного числа -10 дополнением до двух будет 10:
|
|
|
