 |
Арифметические операции над числами в различных системах счисления.
|
|
|
|
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию P системы счисления.
Для выполнения арифметических операций в системе счисления с основанием P необходимо иметь соответствующие таблицы сложения и умножения. Для P = 2, 8 и 16 таблицы представлены ниже.
Двоичная арифметика Таблица 5.
|
| |||||||||||||||||||||
| Восьмеричная арифметика Таблица 6. | ||||||||||||||||||||||
|
|
Шестнадцатеричная арифметика Таблица 7.
|
|
Следует помнить, что при сложении 0F с 1 в шестнадцатеричной системе счисления получаем 10, т.е. происходит перенос. При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий
Пример. Выполнить сложение двоичных чисел:
а) X=1101, Y=101;
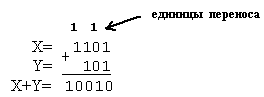
Результат 1101+101=10010.
б) X=1101, Y=101, Z=111;
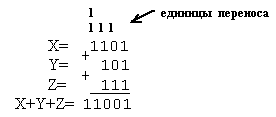
Результат 1101+101+111=11001.
При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.
Пример. Заданы двоичные числа X=10010 и Y=101. Вычислить X-Y.
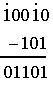
Результат 10010 - 101=1101.
Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.
Пример. 1001 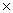 101=?
101=?
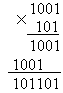
Результат 1001  101=101101.
101=101101.
Упражнения.
1. Перевести следующие числа в десятичную систему счисления:
а) 1101112; б) 10110111.10112; в) 563.448; г) 721.358; д) 1C4.A16; е) 9A2F.B52.
2. Перевести следующие числа из "10" с.с в "2", "8", "16" с.с.:
а) 463; б) 1209; в) 362; г) 3925; д) 11355.
3. Перевести следующие числа из "10" с.с в "2", "8", "16" с.с. (точность вычислений - 5 знаков после точки):
а) 0.0625; б) 0.345; в) 0.225; г) 0.725; д) 217.375; е) 31.2375; ж) 725.03125; з) 8846.04.
4. Перевести следующие числа в двоичную систему счисления:
а) 1725.3268; б) 341.348; в) 7BF.52A16; г) 3D2.C16.
5. Перевести следующие числа из одной системы счисления в другую:
а) 11011001.010112 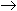 "8" с.с.;
"8" с.с.;
б) 1011110.11012 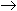 "8" с.с.;
"8" с.с.;
в) 1101111101.01011012 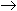 "16" с.с.;
"16" с.с.;
г) 110101000.1001012 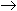 "16" с.с.
"16" с.с.
6. Перевести следующие числа из одной системы счисления в другую:
а) 312.78 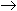 "16" с.с.; б) 51.438
"16" с.с.; б) 51.438 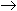 "16" с.с.;
"16" с.с.;
в) 5B.F16 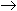 "8" с.с.; г) D4.1916
"8" с.с.; г) D4.1916 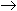 "8" с.с.
"8" с.с.
7. Заданы двоичные числа X и Y. Вычислить X+Y и X-Y, если:
а) X=1101001; Y=101111;
б) X=101110110; Y=10111001;
в) X=100011001; Y=101011.
Лабораторная работа.
ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ ЦЕЛОЧИСЛЕННЫХ
ДАННЫХ В IBM PC
Цель работы
Выполнить перевод заданных преподавателем чисел из десятичной в двоичную и шестнадцатеричную системы счисления. Дать их внутренне (машинное) представление в соответствии с диапазоном в знаковых и беззнаковых форматах типов ShortInt (signed char), Byte (unsigned char), Integer (int), Word (unsigned int). Машинное представление данных должно быть дано в двоичной и шестнадцатеричной системах счисления.
|
|
|
Порядок работы
1. Вычислить для своего варианта целые числа.
2. Перевести их из 10-тичной в 2-ичную и 16-ричную системы счисления.
3. Получить их внутренне представление.
4. Проверить правильность своих выкладок.
В отчете по лабораторной работе должен быть представлен подробный протокол перевода всех заданных чисел из 10-тичной в 2-ичную и 16-ричную системы счисления.
Варианты задания.
Преподавтель задает два базовых числа ± Х и ± Y. Студент должен прибавить и отнять от них номер своего варианта.
Например, пусть Х=±4567, Y=±60, №=45. Тогда получается следующие восемь целых чисел для варианта №=45, а именно:
1) 4567 + 45 = 4612;
2) 4567 - 45 = 4522;
3) -4567 + 45 = -4522;
4) -4567 - 45 = -4612;
5) 60 + 45 = 105;
6) 60 - 45 = 15;
7) - 60 + 45 = - 15;
8) - 60 - 45 = - 105;
|
|
|


