2.1 Расчет параметров уравнений линейной и нелинейной парной регрессии

2. 1 Расчет параметров уравнений линейной и нелинейной парной регрессии

2. 1. 1 Расчет параметров линейной парной регрессии

Парная линейная регрессия имеет вид:

ŷ _x = a + b · x,

где ŷ _x – результативный признак, характеризующий экспорт; x – фактор (импорт);

a, b – параметры, подлежащие определению.

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессии используется метод наименьших квадратов. Он позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака (экспорт товаров) y от теоретических ŷ _x будет минимальной. В этом случае для определения параметров a и b линейной регрессии необходимо решить следующую систему уравнений:

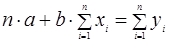
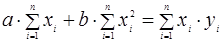
На основании исходных данных выполнены расчеты, которые при = 12 представлены в табл. 1. 1

Таблица 1. 1

Номер п. п.								%
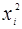
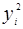
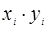
	11, 7	21, 5	136, 890	462, 250	251, 550	20, 267	1, 233	5, 734
	14, 1	23, 6	198, 810	556, 960	332, 760	23, 481	0, 119	0, 502
		26, 6	289, 000	707, 560	452, 200	27, 365	0, 765	2, 877
	16, 7	27, 2	278, 890	739, 840	454, 240	26, 964	0, 236	0, 869
	17, 5	29, 7	306, 250	882, 090	519, 750	28, 035	1, 665	5, 606
	18, 6	26, 9	345, 960	723, 610	500, 340	29, 508	2, 608	9, 696
	19, 4	29, 9	376, 360	894, 010	580, 060	30, 580	0, 680	2, 273
	20, 1	31, 1	404, 010	967, 210	625, 110	31, 517	0, 417	1, 341
	18, 8	28, 5	353, 440	812, 250	535, 800	29, 776	1, 276	4, 477
	22, 2	34, 8	492, 840	1211, 040	772, 560	34, 330	0, 470	1, 352
	22, 6	36, 1	510, 760	1303, 210	815, 860	34, 865	1, 235	3, 420
	24, 8	38, 6	615, 040	1489, 960	957, 280	37, 812	0, 788	2, 042
Сумма	223, 500	354, 500	4308, 250	10749, 990	6797, 510	-	-	-
Среднее значение	18, 625	29, 542	359, 021	895, 833	566, 459	-	-	-

 

С учетом обозначений при n = 12

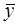 = (y₁ + y₂ + … + y₁₂)/12; = (x₁ + x₂ + … + x₁₂)/12;

 = (y₁x₁ + y₂x₂ + … + y₁₂ x₁₂)/12;

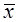= (x₁² + x₂² + … + x₁₂)/12; S_x² = ².

Значения параметров линейной регрессии вычисляются по формулам:

b = ( 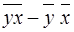)/( 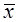²) = (566, 459 – 29, 542× 18, 625) / (359, 021– 18, 625 × 18, 625) = 1, 3393;

a = 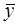 – b  = 29, 542– 1, 3393× 18, 625= 4, 5978.

 

Тогда уравнение регрессии, являющееся линейной моделью импорта в зависимости от экспорта, примет вид:

ŷ _x = 4, 5978 + 1, 3393 · x.

На Рис. 5 представлены опытные значения импорта и экспорта товаров, а также теоретические значения импорта за 12 месяцев.

 

Рис. 1. 5

 

На Рис. 6 выполнено построение линейной функции регрессии.

 

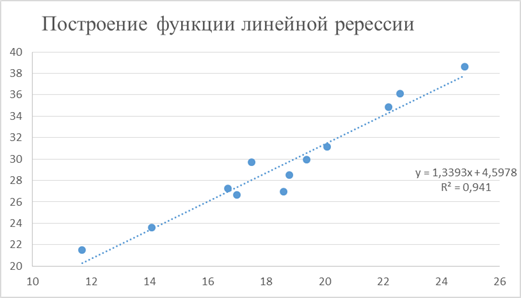
Рис. 1. 6

2. 1. 2 Расчет параметров степенной парной регрессии

Степенная парная регрессия относится к нелинейным регрессиям по оцениваемым параметрам. Однако она считается внутренне линейной, так как логарифмирование ее приводит к линейному виду. Таким образом, построению степенной модели

предшествует процедура линеаризации переменных. Линеаризация позволяет использовать для определения параметров функции регрессии метод наименьших квадратов. При этом оценки параметров будут вычислены по алгоритму, изложенному в 2. 1. 1.

для этой цели проведем логарифмирование обеих частей уравнения:

lg ŷ = lg a + b lg x.

Обозначим через Ŷ = lg ŷ ; X = lg x; A = lg a. Тогда уравнение примет вид:

Ŷ = A + b X.

 Как отмечалось, для расчета параметров А и b используются соотношения метода наименьших квадратов, поскольку в новых переменных Y и X соотношение стало линейным, аследовательно, оценки параметров будут состоятельными, несмещенными и эффективными.

Весь предварительный расчет параметров степенной функции регрессии аналогично линейной сведен в табл. 1. 2.

Таблица 1. 2

 

Номер п/п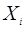
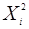
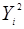
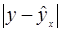
	2, 460	3, 068	6, 050	9, 413	7, 546	20, 466	1, 034	4, 810
	2, 646	3, 161	7, 002	9, 993	8, 365	23, 730	0, 130	0, 552
	2, 833	3, 281	8, 027	10, 764	9, 296	27, 526	0, 926	3, 479
	2, 815	3, 303	7, 927	10, 911	9, 300	27, 140	0, 060	0, 222
	2, 862	3, 391	8, 192	11, 500	9, 706	28, 166	1, 534	5, 166
	2, 923	3, 292	8, 545	10, 838	9, 623	29, 561	2, 661	9, 893
	2, 965	3, 398	8, 793	11, 545	10, 076	30, 565	0, 665	2, 225
	3, 001	3, 437	9, 004	11, 814	10, 314	31, 437	0, 337	1, 083
	2, 934	3, 350	8, 608	11, 222	9, 828	29, 813	1, 313	4, 607
	3, 100	3, 550	9, 611	12, 600	11, 004	34, 015	0, 785	2, 256
	3, 118	3, 586	9, 722	12, 861	11, 182	34, 500	1, 600	4, 431
	3, 211	3, 653	10, 310	13, 346	11, 730	37, 138	1, 462	3, 787
Сумма	34, 868	40, 471	101, 789	136, 809	117, 970	-	-	-
Среднее значение	2, 906	3, 373	8, 482	11, 401	9, 831	-	-	-

 

Тогда

b = ( – 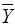)/S_x² = (9, 831 – 3, 373·2, 906)/( 11, 401 – 2, 906·2, 906) = 1, 17351;

A = 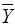 – b ·  = 3, 373 – 1, 17351·2, 906= -0, 0373.

Таким образом, степенное уравнение регрессии с учетом логарифмических переменных будет иметь вид:

Ŷ = -0, 0373+ 1, 17351·X.

Выполнив его потенцирование, получим:

ŷ _x = 2, 909 x ^{0, 7932}

Подставляя в последнее уравнение фактические значения x, получаем теоретическое значение ŷ _x. Эти значения приведены в табл. 2. 2.

    На Рис. 7 представлены опытные значения опытные значения экспорта, млрд $ и импорта, млрд $, а также теоретические значения импорта за 12 месяцев. На Рис. 8 выполнено построение степенной функции регрессии.

Рис. 1. 7

 

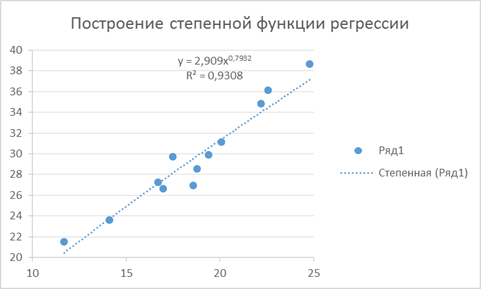
Рис. 1. 8

 

2. 1. 3 Расчет параметров показательной парной регрессии

Поскольку показательная функция относится к классу нелинейных по оцениваемым параметрам, то построению функции парной показательной регрессии

ŷ _x = a·b^x

предшествует, как и в случае степенной функции регрессии, процедура линеаризации переменных с помощью логарифмирования обеих частей функции регрессии. После логарифмирования получим следующее выражение:

lg ŷ _х =lg a + x lg b.

Введя обозначения переменных и констант

Ŷ = lg ŷ _х, A = lg a, B = lg b,

получим линейное уравнение регрессии в новых переменных:

Ŷ = A + B x.

Для определения параметров все вычисления сведены в табл. 1. 3.

Таблица 1. 3

 

Номер п/п	x	Y	x × Y	x2	Y2
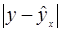
	11, 7	3, 068	35, 896	136, 890	9, 413	21, 293	0, 207	0, 964
	14, 1	3, 161	44, 574	198, 810	9, 993	23, 774	0, 174	0, 738
		3, 281	55, 775	289, 000	10, 764	27, 161	0, 561	2, 110
	16, 7	3, 303	55, 164	278, 890	10, 911	26, 790	0, 410	1, 509
	17, 5	3, 391	59, 345	306, 250	11, 500	27, 792	1, 908	6, 424
	18, 6	3, 292	61, 234	345, 960	10, 838	29, 232	2, 332	8, 670
	19, 4	3, 398	65, 918	376, 360	11, 545	30, 326	0, 426	1, 426
	20, 1	3, 437	69, 088	404, 010	11, 814	31, 317	0, 217	0, 699
	18, 8	3, 350	62, 978	353, 440	11, 222	29, 502	1, 002	3, 516
	22, 2	3, 550	78, 802	492, 840	12, 600	34, 488	0, 312	0, 896
	22, 6	3, 586	81, 050	510, 760	12, 861	35, 128	0, 972	2, 693
	24, 8	3, 653	90, 601	615, 040	13, 346	38, 863	0, 263	0, 681
Сумма	223, 5	40, 471	760, 425	4308, 250	136, 809
Среднее значение	18, 625	3, 373	63, 369	359, 021	11, 401

 

C учетом табличных данных значения параметров линейной регрессии составят:

B =  / S_x² = (63, 369 – 3, 373× 18, 625)/12, 130= 0, 04572;

A =  – B  = 3, 373 – 0, 004572× 18, 625 = 2, 521.

Таким образом, получено уравнение

Ŷ = 2, 521 + 0, 04572x,

или после потенцирования

ŷ _x = 12, 441 (1, 047) ^x.

На Рис. 9 представлены опытные значения экспорта и импорта товаров в 2007 году, а также теоретические значения экспорта. На Рис. 10 выполнено построение показательной функции регрессии.

 

Рис. 1. 9

 

Рис. 1. 10

На Рис. 1. 11 и Рис. 1. 12 представлены все построенные функции регрессии

        

 

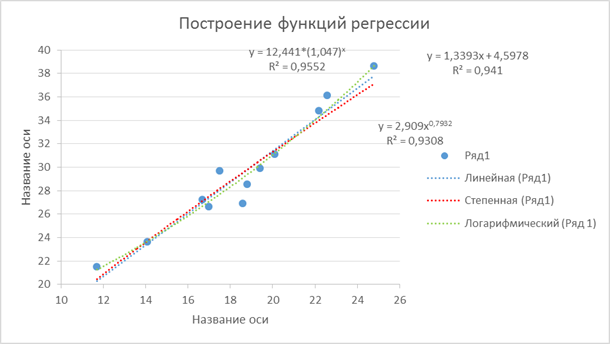
Рис. 1. 11

 

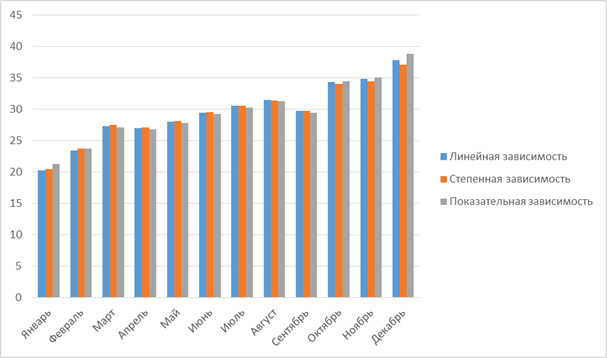
    Рис. 12

 

Построенная функция регрессии дает возможность рассчитывать прогнозные значения средних экспорта товаров (𝑦 ̂ 𝑥 ) при импорте товаров (x). Парная линейная регрессия, судя по графику (рис. 1. 11), расположена достаточно близко к опытным данным. В первом приближении можно принять парную линейную регрессию для расчета прогнозных значений потребительских расходов в расчете на душу населения. Вместе с тем, для более точной оценки качества и статистической значимости регрессии следует использовать известные статистические критерии.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: