2.5 Сравнительная оценка силы связи импорта с экспортом с помощью среднего коэффициента эластичности

2. 5 Сравнительная оценка силы связи импорта с экспортом с помощью среднего коэффициента эластичности

 

Средний коэффициент эластичности Э показывает, на сколько процентов в среднем изменится цена на жилье на первичном рынке жилья ŷ _x от своей величины при изменении себестоимости строительства x на 1% от своего значения. Для произвольной величины x он может быть вычислен по следующей формуле:

Э = y_x' (x)· 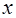/ ŷ _x.

С учетом приведенной формулы коэффициент эластичности Э для линейной функции регрессии

ŷ _x = 16, 883 + 0, 698 × x

примет следующий вид:  

Э = ŷ _x' (x) · 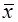/ ŷ _x= b · / (a + b ).

В таблице 5. 1 вычислены коэффициент эластичности для линейной функции регрессии.

Таблица 5. 1

№ п/п	x	y	ŷ	A	ŷ ’	Эy(x)
	11, 7	21, 5	20, 267	5, 734	1, 339	0, 773
	14, 1	23, 6	23, 481	0, 502	1, 339	0, 804
		26, 6	27, 365	2, 877	1, 339	0, 832
	16, 7	27, 2	26, 964	0, 869	1, 339	0, 829
	17, 5	29, 7	28, 035	5, 606	1, 339	0, 836
	18, 6	26, 9	29, 508	9, 696	1, 339	0, 844
	19, 4	29, 9	30, 580	2, 273	1, 339	0, 850
	20, 1	31, 1	31, 517	1, 341	1, 339	0, 854
	18, 8	28, 5	29, 776	4, 477	1, 339	0, 846
	22, 2	34, 8	34, 330	1, 352	1, 339	0, 866
	22, 6	36, 1	34, 865	3, 420	1, 339	0, 868
	24, 8	38, 6	37, 812	2, 042	1, 339	0, 878
Среднее значение	18, 625	29, 542	29, 542	3, 349083	1, 339	0, 840

 

Аналогичные расчеты коэффициентов эластичности выполнены для степенной и для показательной функций. На Рис. 5. 1 приведены их значения. Анализ разработанных математических моделей показывает, что изменение на 1% импорта, например, импорт в январе, приводит к увеличению на 1, 879 … 1, 766% экспорта.

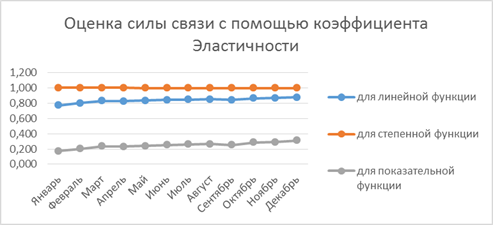
Рис. 5. 1

 

 

2. 6 Оценка статистической надежности результатов линейного регрессионного моделирования

Оценку статистической надежности уравнения регрессии в целом будем производить с помощью F-критерия Фишера. При этом примем нулевую гипотезу H₀, что коэффициент регрессии b равен нулю. В таком случае фактор x не оказывает влияния на результат y, то есть себестоимость строительства не оказывает влияния на цены на жилья на первичном рынке. Альтернативная гипотеза H₁ будет состоять в статистической надежности линейного регрессионного моделирования. Для установления истинной значимости линейной модели необходимо выполнить сравнение факторного F_факт  и критического (табличного) F_табл значений F-критерия Фишера. Факторный F-критерий Фишера вычисляется по формуле:

F_факт = S_факт² / S_ост²,

где S_факт² – факторная выборочная дисперсия, вычисленная на одну степень свободы по соотношению:

 

S_факт² = ((ŷ _x1 – 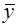)² + (ŷ _x2 – 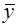)²  +... + (ŷ _x12 – 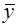)²) / 1;

S_ост² – остаточная выборочная дисперсия, вычисленная на одну степень свободы по соотношению:

S_ост² = ( (y₁ – ŷ _x1)² + (y₂ – ŷ _x2)²  +... + (y₁₇ – ŷ _x12)² )/ n – 2.

Если нулевая гипотеза справедлива, то факторная и остаточная выборочные дисперсии не отличаются друг от друга. Для опровержения нулевой гипотезы H₀ необходимо, чтобы факторная дисперсия превышала остаточную дисперсию в несколько раз. Табличное F_табл значение F-критерия Фишера – это максимальная величина критерия (отношения дисперсий) под влиянием случайных факторов при данных степенях свободы и уровне значимости α, который примем равным 0, 05.

Если F_табл < F_факт, то нулевая гипотеза о случайной природе коэффициента регрессии, а следовательно, и оцениваемой модели отвергается и признается их статическая значимость и надежность. Если F_табл > F_факт, то нулевая гипотеза не отклоняется и признается статическая незначимость и ненадежность уравнения регрессии.

По таблице значений F-критерия Фишера при уровне значимости α = 0, 05 и степенях свободы к₁ = 1, к₂ = 10 получаем F_табл = 4, 965. Выполнив расчет, получим F_факт = 159, 492.

Полученные значения F-критерия Фишера указывают, что       F_табл < F_факт , поэтому необходимо отвергнуть нулевую гипотезу о случайной природе коэффициента регрессии, а следовательно, и оцениваемой модели и принять альтернативную гипотезу.

 

2. 7 Расчет прогнозного значения экспорта по линейной модели при увеличении импорта

Полученное уравнение линейной регрессии позволяет использовать его для прогноза. Согласно заданию на курсовую работу, следует рассчитать прогнозное значение экспорта, если прогнозное значение импорта увеличится на 10% от среднего значения всего импорта. При этом установить доверительный интервал прогноза для уровня значимости, равного 0, 05.

Если прогнозное значение импорта строительства составит

x_p = 1, 1 · 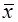= 1, 1 · 18, 625= 20. 488,

то прогнозное точечное значение экспорта можно вычислить по соотношению:

ŷ _xp = 4, 5978 + 1, 3393 · x_p = 4, 5978 + 1, 3393 · 20, 488= 32, 037.

 

Для определения доверительного интервала прогноза цен необходимо вычислить ошибку прогноза по формуле:

m_{ŷ p} = S_ост·(1 + 1 / 12 + ( x_p – 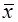)²/( (x₁ – 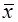)² + (x₂ – 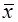)² + ... + (x₇ –

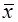– )²))^1/2 = 4, 047 ·(1 + 1/12 + (20, 488 – 18, 625)² / ( (11, 7 –

– 18, 625)² + (14, 1 – 18, 625)² +...

…+ (24, 8 – 18, 625²))^1/2 = 4, 258.

Предельная ошибка прогноза, которая с вероятностью 0, 95 не будет превышена, составит:

∆ _{ŷ p} = t_табл · m_{ŷ p} = 2, 228· 4, 258 = 9, 487.

Здесь t_табл – табличное значение t-статистки Стьюдента для числа степеней свободы n – 2 = 10 и уровне значимости 0, 05.

Тогда предельные значения доверительного интервала прогноза экспорта при прогнозируемом увеличении импорта на 10% можно вычислить по формулам:

ŷ _{xp min} = ŷ _xp – ∆ _{ŷ p} = 32, 037 – 9, 487 = 22, 550;

ŷ _{xp max} =  ŷ _xp + ∆ _{ŷ p} = 32, 037 + 9, 487 = 41, 524.

Выполненный прогнозный расчет по линейной регрессионной модели показал, что при достаточной надежности (вероятность 0, 95) прогнозируемое значение ŷ _xp = 32, 037 будет накрыто диапазоном (22, 550 – 41, 524).

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: