 |
2.2 Дисперсионный анализ линейной функции регрессии
|
|
|
|
2. 2 Дисперсионный анализ линейной функции регрессии
Центральное место в дисперсионном анализе занимает разложение общей суммы квадратов отклонения результирующего показателя y от его среднего значения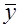 
на две части, а именно на объясненную (факторную) и остаточную:
, (*)
где 
– общая сумма квадратов отклонений;
– объясненная (факторная) сумма квадратов;
– остаточная сумма квадратов.
Результаты расчетов сведены в табл. 2. 1.
Таблица 2. 1
| Номер п/п | yi | | yi –  |
| (yi – )2
| ŷ xi | | ŷ xi – |
| (ŷ xi – )2
| | yi – ŷ xi | | (yi – ŷ xi)2 |
| 21, 5 | -8, 042 | 64, 668 | 20, 267 | -9, 274 | 86, 015 | 1, 233 | 1, 520 | |
| 23, 6 | -5, 942 | 35, 303 | 23, 481 | -6, 060 | 36, 726 | 0, 119 | 0, 014 | |
| 26, 6 | -2, 942 | 8, 653 | 27, 365 | -2, 176 | 4, 736 | -0, 765 | 0, 586 | |
| 27, 2 | -2, 342 | 5, 483 | 26, 964 | -2, 578 | 6, 647 | 0, 236 | 0, 056 | |
| 29, 7 | 0, 158 | 0, 025 | 28, 035 | -1, 507 | 2, 270 | 1, 665 | 2, 772 | |
| 26, 9 | -2, 642 | 6, 978 | 29, 508 | -0, 033 | 0, 001 | -2, 608 | 6, 803 | |
| 29, 9 | 0, 358 | 0, 128 | 30, 580 | 1, 038 | 1, 077 | -0, 680 | 0, 462 | |
| 31, 1 | 1, 558 | 2, 428 | 31, 517 | 1, 975 | 3, 902 | -0, 417 | 0, 174 | |
| 28, 5 | -1, 042 | 1, 085 | 29, 776 | 0, 234 | 0, 055 | -1, 276 | 1, 628 | |
| 34, 8 | 5, 258 | 27, 650 | 34, 330 | 4, 788 | 22, 924 | 0, 470 | 0, 221 | |
| 36, 1 | 6, 558 | 43, 012 | 34, 865 | 5, 324 | 28, 341 | 1, 235 | 1, 525 | |
| 38, 6 | 9, 058 | 82, 053 | 37, 812 | 8, 270 | 68, 393 | 0, 788 | 0, 621 | |
| Сумма | 354, 500 | 277, 466 | 354, 500 | 261, 087 | 16, 382 | |||
| Среднее значение | 29, 542 | 23, 122 | 29, 542 | 21, 757 | 1, 365 |
На основании выполненных расчетов имеем: 277, 469 = 261, 087 + 16, 382. Следовательно равенство (*) выполняется.
Если коэффициент b изменить в 1, 1 раза, то измененное уравнение линейной регрессии будет иметь вид: ŷ x = 4, 5978 + 1, 47323 · x и приведенное выше соотношение (*) выполняться не будет, что следует из расчетов (табл. 2. 2).
|
|
|
Таблица 2. 2
| Номер п/п | yi | | yi –  |
| (yi – )2
| ŷ xi | | ŷ xi – |
| (ŷ xi – )2
| | yi – ŷ xi | | (yi – ŷ xi)2 |
| 21, 5 | -8, 042 | 64, 668 | 21, 835 | -7, 707 | 59, 399 | -0, 335 | 0, 112 | |
| 23, 6 | -5, 942 | 35, 303 | 25, 370 | -4, 171 | 17, 400 | -1, 770 | 3, 134 | |
| 26, 6 | -2, 942 | 8, 653 | 29, 643 | 0, 101 | 0, 010 | -3, 043 | 9, 258 | |
| 27, 2 | -2, 342 | 5, 483 | 29, 201 | -0, 341 | 0, 116 | -2, 001 | 4, 003 | |
| 29, 7 | 0, 158 | 0, 025 | 30, 379 | 0, 838 | 0, 702 | -0, 679 | 0, 461 | |
| 26, 9 | -2, 642 | 6, 978 | 32, 000 | 2, 458 | 6, 043 | -5, 100 | 26, 009 | |
| 29, 9 | 0, 358 | 0, 128 | 33, 178 | 3, 637 | 13, 226 | -3, 278 | 10, 748 | |
| 31, 1 | 1, 558 | 2, 428 | 34, 210 | 4, 668 | 21, 791 | -3, 110 | 9, 670 | |
| 28, 5 | -1, 042 | 1, 085 | 32, 295 | 2, 753 | 7, 578 | -3, 795 | 14, 398 | |
| 34, 8 | 5, 258 | 27, 650 | 37, 304 | 7, 762 | 60, 246 | -2, 504 | 6, 268 | |
| 36, 1 | 6, 558 | 43, 012 | 37, 893 | 8, 351 | 69, 741 | -1, 793 | 3, 214 | |
| 38, 6 | 9, 058 | 82, 053 | 41, 134 | 11, 592 | 134, 380 | -2, 534 | 6, 421 | |
| Сумма | 354, 500 | 277, 469 | 390, 633 | 93, 697 | ||||
| Средн. зн. | 29, 542 | 23, 122 | 32, 553 | 7, 808 |
Из таблицы следует:
277, 469 ≠ 390, 633+93, 697,
т. е. 
.
На Рис. 2. 1 результаты дисперсионного анализа для линейной функции регрессии представлены графически.
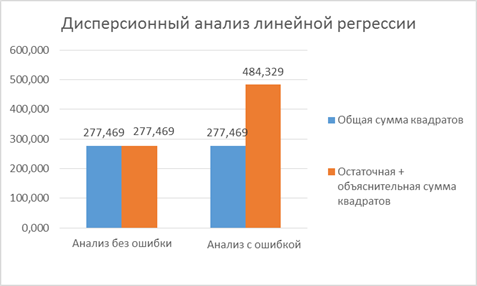
Рис. 2. 1
В результате проделанной работы, были освоены навыки математического соотношения характеристик дисперсионного анализа линейной функции регрессии. Было доказано, что оценка общей дисперсии 𝑆 𝑦 общ 2 состоит из оценки дисперсии объясненной 𝑆 𝑦 объясн 2 и оценки дисперсии остатков 𝑆 𝑦 остат 2. На основании выполненных расчетов мы получили равенство: 277, 469 = 261, 087 + 16, 382.
При изменении коэффициента 𝑏 в 1. 1 раза, то измененное уравнение линейной регрессии будет иметь вид: Ŷ ᵪ = 4, 5978 + 1, 47323 · x, и приведенное выше соотношение выполняться не будет.
2. 3 Оценка тесноты связи экспорт и импорта с помощью показателей корреляции и детерминации
|
|
|
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Существуют различные формы записи линейного коэффициента корреляции. Наиболее часто встречаются следующие:
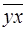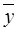
rxy = b (Sx / Sy) = Mxy /(Sx / Sy) = ( 
– 
)/ SxSy.
Как известно, линейный коэффициент корреляции находится в пределах –1 ≤ rxy ≤ 1. Если коэффициент регрессии b > 0, то 0 ≤ rxy ≤ 1, и наоборот, при b < 0 –1 ≤ rxy ≤ 0.
Используя первое выражение для rxy, рассчитаем линейный коэффициент парной корреляции:
rxy = b (Sx/Sy) =1, 3393 (3, 4828/4, 8086) = 0, 970.
Значение коэффициента корреляции показывает, что связь прямая, то есть с увеличением импорта, экспорт увеличивается.
Для оценки качества подбора линейной функции необходимо определить квадрат линейного коэффициента rxy2, который называется коэффициентом детерминации линейной функции регрессии. Он характеризует долю дисперсии (разброса) цен на жилье на первичном рынке ŷ x, объясняемую зависимостью от себестоимости строительства x, в общей дисперсии, возникающей за счет влияния множества факторов, не учтенных функцией регрессии.
Соответственно величина 1 – rxy2 характеризует долю дисперсии экспорта y, вызванную влиянием остальных не учтенных в математической модели факторов.
Определим коэффициент детерминации:
ryx2 = ( 0, 970 )2 = 0, 941.
Следовательно, изменение экспорта на 94, 1% объясняется изменением импорта.
2. 4 Оценка ошибки аппроксимации уравнений регрессии
Из графиков и приведенных в таблицах расчетных данных следует, что фактическое значение экспорта y отличается от теоретического значения ŷ x, рассчитанных по одному из уравнений регрессии. Очевидно, чем меньше это отличие, тем ближе опытные данные к теоретическим значениям и тем лучше качество модели.
Величина, представляющая собой разность опытного и теоретического результативного признака (y – ŷ x ) для каждого опыта представляет собой ошибку аппроксимации функции, связывающей экспорт и импорт. В данном случае число таких опытов равно двенадцати. Для оценки каждого опыта используются не сами разности, а абсолютные значения разностей опытного и теоретического результативных признаков, отнесенные к опытному признаку и выраженные в процентах, то есть:
|
|
|
Аi = | (yi – ŷ xi) / yi |100%.
Таблица 4. 1
|
№ п/п | Линейная регрессия | Степенная регрессия | Показательная регрессия | |||
| |yi – ŷ xi|2 |
| |yi – ŷ xi|2 |
| |yi – ŷ xi|2 |
| |
| 1, 520 | 5, 734 | 1, 069 | 4, 810 | 0, 043 | 0, 964 | |
| 0, 014 | 0, 502 | 0, 017 | 0, 552 | 0, 030 | 0, 738 | |
| 0, 585 | 2, 877 | 0, 857 | 3, 479 | 0, 315 | 2, 110 | |
| 0, 056 | 0, 869 | 0, 004 | 0, 222 | 0, 168 | 1, 509 | |
| 2, 772 | 5, 606 | 2, 353 | 5, 166 | 3, 640 | 6, 424 | |
| 6, 802 | 9, 696 | 7, 081 | 9, 893 | 5, 438 | 8, 670 | |
| 0, 462 | 2, 273 | 0, 442 | 2, 225 | 0, 181 | 1, 426 | |
| 0, 174 | 1, 341 | 0, 114 | 1, 083 | 0, 047 | 0, 699 | |
| 1, 628 | 4, 477 | 1, 724 | 4, 607 | 1, 004 | 3, 516 | |
| 0, 221 | 1, 352 | 0, 616 | 2, 256 | 0, 097 | 0, 896 | |
| 1, 525 | 3, 420 | 2, 560 | 4, 431 | 0, 945 | 2, 693 | |
| 0, 621 | 2, 042 | 2, 137 | 3, 787 | 0, 069 | 0, 681 | |
| Ср. зн. | 1, 365 | 3, 349 | 1, 581 | 3, 543 | 0, 998 | 2, 527 |
Оценка качества всей функции регрессии может быть осуществлена как средняя ошибка аппроксимации – средняя арифметическая Аi:
А = (А1 + А2 + … + А12 ) / 12.
Найдем величину средней ошибки аппроксимации линейной функции связи между ценами на жилье на первичном рынке и себестоимостью строительства:
А = 40, 189 · 100% / 12 = 3, 349 %.
Аналогично получим среднюю ошибку аппроксимации для степенной:
А = 42, 511/12 = 3, 543%
и для показательной функции: А = 30, 326/12 = 2, 572%.
Их анализ показывает, что ошибка аппроксимации находится в допустимых для практического использования пределах, однако с теоретической точки зрения может быть продолжен поиск более качественной функции регрессии. Ниже приводятся графики ошибки аппроксимации линейной, степенной и показательной регрессий.
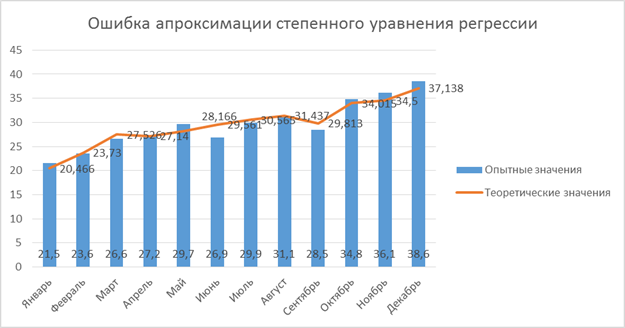
Рис. 4. 1
Рис. 4. 2
Рис. 4. 3
|
|
|
