Главная | Обратная связь | Поможем написать вашу работу!

Часть 3 – популяционное распределение величины соционических функций внутри ТИМа

Напомним (см. работу [17]), что величины всех 8-ми соционических функций испытуемого вычисляются как сумма произведений соответствующей функции строки коэффициентов в нижеприведенной таблице 7 на типные нагрузки из строки типного профиля испытуемого. Если типный профиль нормирован к единичному стандартному отклонению нагрузок типного профиля, то в результате умножения и функциональный профиль получается квазинормированным, то есть близким к единичному стандартному отклонению в массиве значений всех 8-ми функций.

Таким образом, выраженные в виде нормированных типных профилей результаты всех испытуемых выборки могут быть преобразованы в функциональные профили этих испытуемых, вслед за чем, разумеется, можно построить диаграммы распределения величин функций в экспериментальной выборке (в зависимости от названия функций, либо их позиции внутри ТИМа, и т.п.)

Табл.7. Коэффициенты для расчета величины функций по типному профилю испытуемого (функция вычисляется как сумма произведений элементов соответствующей строки настоящей таблицы на строку нагрузок типного профиля). Для расчета значений функций внутри конкретного «стандартного» ТИМа соответствующая строка табл.7 умножается (то есть ищется сумма произведений) на соответствующую нужному ТИМу строку из табл. 1 либо табл.4. (в зависимости от того, используем мы типный профиль в метрике диагностических корреляций либо в метрике их квадратов, то есть т.н. «типных общностей»)

	ИЛЭ	ЛИИ	СЭИ	ЭСЭ	СЛЭ	ЛСИ	ИЭИ	ЭИЭ	СЭЭ	ЭСИ	ИЛИ	ЛИЭ	ИЭЭ	ЭИИ	СЛИ	ЛСЭ
БИ	-0,0625	-0,0625	0,0107	-0,2393	-0,0625	-0,0625	0,3643	0,1143	-0,0625	-0,0625	0,3643	0,1143	-0,0625	-0,0625	0,0107	-0,2393
ЧИ	0,3643	0,1143	-0,0625	-0,0625	0,0107	-0,2393	-0,0625	-0,0625	0,0107	-0,2393	-0,0625	-0,0625	0,3643	0,1143	-0,0625	-0,0625
БС	-0,0625	-0,0625	0,3643	0,1143	-0,0625	-0,0625	0,0107	-0,2393	-0,0625	-0,0625	0,0107	-0,2393	-0,0625	-0,0625	0,3643	0,1143
ЧС	0,0107	-0,2393	-0,0625	-0,0625	0,3643	0,1143	-0,0625	-0,0625	0,3643	0,1143	-0,0625	-0,0625	0,0107	-0,2393	-0,0625	-0,0625
БЛ	0,1143	0,3643	-0,0625	-0,0625	0,1143	0,3643	-0,0625	-0,0625	-0,2393	0,0107	-0,0625	-0,0625	-0,2393	0,0107	-0,0625	-0,0625
ЧЛ	-0,0625	-0,0625	-0,2393	0,0107	-0,0625	-0,0625	-0,2393	0,0107	-0,0625	-0,0625	0,1143	0,3643	-0,0625	-0,0625	0,1143	0,3643
БЭ	-0,2393	0,0107	-0,0625	-0,0625	-0,2393	0,0107	-0,0625	-0,0625	0,1143	0,3643	-0,0625	-0,0625	0,1143	0,3643	-0,0625	-0,0625
ЧЭ	-0,0625	-0,0625	0,1143	0,3643	-0,0625	-0,0625	0,1143	0,3643	-0,0625	-0,0625	-0,2393	0,0107	-0,0625	-0,0625	-0,2393	0,0107

Диаграммы распределения величины функций, рассчитанных по типным профилям, составленным из диагностических корреляций, нормированных по 1-му способу (к единичному стандартному отклонению нагрузок типного профиля). Все функциональные профили (индивидуальные наборы 8-ми функций в ТИМе испытуемых) перед построением диаграмм дополнительно нормализованы (делением на стандартное отклонение функционального профиля) вплоть до приведения всех функциональных профилей к единичному стандартному отклонению.

Рис.22.1. Распределение величины программной функции в экспериментальной выборке (расчет функций по типным профилям диагностических корреляций, нормированных по способу №1)

Рис.22.2. Распределение величины демонстрационной функции в экспериментальной выборке (расчет функций по типным профилям диагностических корреляций, нормированных по способу №1)

Рис.22.3. Распределение величины контролирующей функции в экспериментальной выборке (расчет функций по типным профилям диагностических корреляций, нормированных по способу №1)

Рис.22.4. Распределение величины творческой функции в экспериментальной выборке (расчет функций по типным профилям диагностических корреляций, нормированных по способу №1)

Рис.22.5. Распределение величины контактной функции в экспериментальной выборке (расчет функций по типным профилям диагностических корреляций, нормированных по способу №1)

Рис.22.6. Распределение величины активационной функции в экспериментальной выборке (расчет функций по типным профилям диагностических корреляций, нормированных по способу №1)

Рис.22.7. Распределение величины суггестивной функции в экспериментальной выборке (расчет функций по типным профилям диагностических корреляций, нормированных по способу №1)

Рис.22.8. Распределение величины мобилизационной функции в экспериментальной выборке (расчет функций по типным профилям диагностических корреляций, нормированных по способу №1)

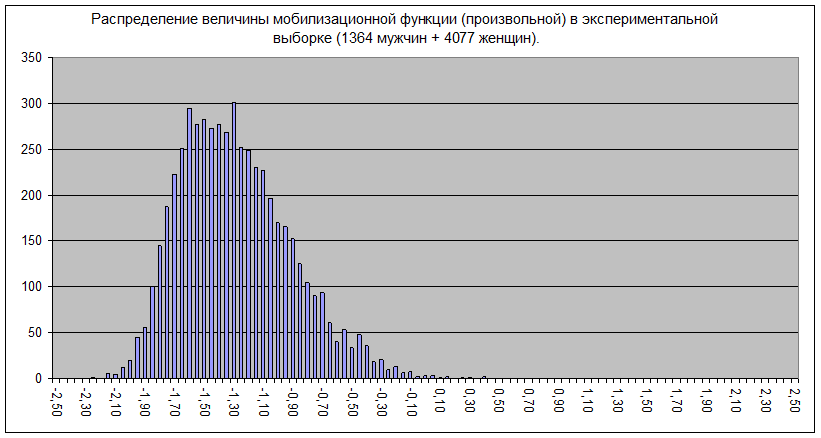
Рис.23.1. Распределение величины функций (всех 8-ми функций ТИМа, независимо от их позиции) в экспериментальной мужской выборке. Расчет функций по типным профилям диагностических корреляций, нормированных по способу №1

Рис.23.2. Распределение величины функций (всех 8-ми функций ТИМа, независимо от их позиции) в экспериментальной женской выборке. Расчет функций по типным профилям диагностических корреляций, нормированных по способу №1

Рис.23.3. Распределение величины функций (всех 8-ми функций ТИМа, независимо от их позиции) в экспериментальной смешанной выборке. Расчет функций по типным профилям диагностических корреляций, нормированных по способу №1

Диаграммы распределения величины функций, рассчитанных по типным профилям, составленным из диагностических типных общностей (квадратов диагностических корреляций со знаком корреляций), нормированных по 1-му способу (к единичному стандартному отклонению нагрузок типного профиля). Все функциональные профили (индивидуальные наборы 8-ми функций в ТИМе испытуемых) перед построением диаграмм дополнительно нормализованы (делением на стандартное отклонение функционального профиля) вплоть до приведения всех функциональных профилей к единичному стандартному отклонению.

Рис.24.1. Распределение величины программной функции в экспериментальной выборке (расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1)

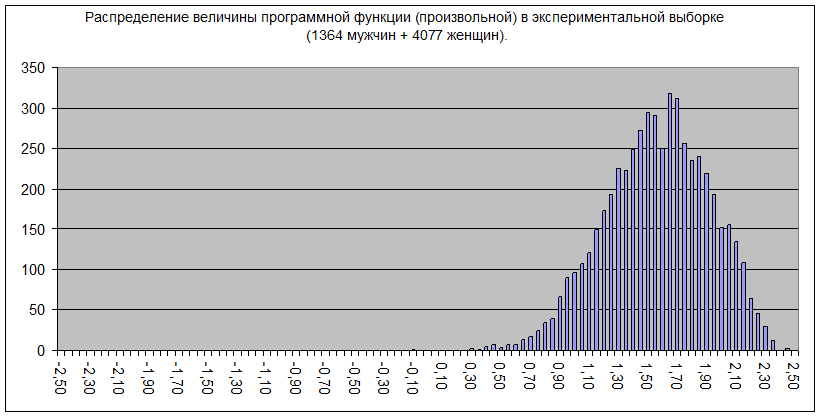
Рис.24.2. Распределение величины демонстрационной функции в экспериментальной выборке (расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1)

Рис.24.3. Распределение величины контролирующей функции в экспериментальной выборке (расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1)

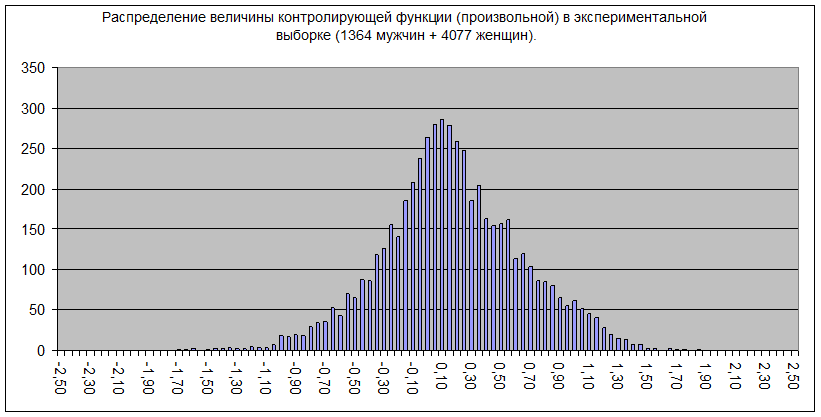
Рис.24.4. Распределение величины творческой функции в экспериментальной выборке (расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1)

Рис.24.5. Распределение величины контактной функции в экспериментальной выборке (расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1)

Рис.24.6. Распределение величины активационной функции в экспериментальной выборке (расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1)

Рис.24.7. Распределение величины суггестивной функции в экспериментальной выборке (расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1)

Рис.24.8. Распределение величины мобилизационной функции в экспериментальной выборке (расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1)

Рис.25.1. Распределение величины функций (всех 8-ми функций ТИМа, независимо от их позиции) в экспериментальной мужской выборке. Расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1

Рис.25.2. Распределение величины функций (всех 8-ми функций ТИМа, независимо от их позиции) в экспериментальной женской выборке. Расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1

Рис.25.3. Распределение величины функций (всех 8-ми функций ТИМа, независимо от их позиции) в экспериментальной смешанной выборке. Расчет функций по типным профилям типных общностей (квадратов диагностических корреляций со знаками), нормированных по способу №1

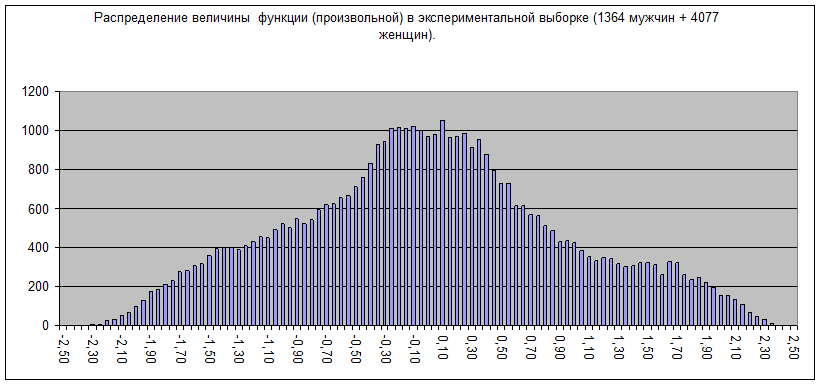
Табл.8. Интегральная таблица характеристик популяционного распределения величин соционических функций внутри ТИМа (функции приведены в порядке убывания их средних величин)

Принятая нумерация функций в ТИМе		Расчет функций по типным профилям из нормированных диагностических корреляций	Расчет функций по типным профилям из нормированных дисперсионных типных общностей (квадратов диагностических корреляций со знаками)
	среднее (М+Ж)	медиана (М+Ж)	мода (М+Ж)	стандотклон (М+Ж)	стандотклон МУЖ	стандотклон ЖЕН	среднее (М+Ж)	медиана (М+Ж)	мода (М+Ж)	стандотклон (М+Ж)	стандотклон МУЖ	стандотклон ЖЕН
	программная ф-я	1,39	1,43	1,55	0,351	0,335	0,356	1,56	1,58	1,65	0,357	0,354	0,357
	демонстрационная ф-я	0,77	0,82	0,95	0,428	0,428	0,429	0,58	0,61	0,75	0,442	0,440	0,443
	контролирующая ф-я	0,31	0,33	0,10	0,562	0,555	0,564	0,17	0,14	0,10	0,475	0,461	0,480
	творческая ф-я	-0,03	-0,03	0,10	0,547	0,531	0,551	0,14	0,20	0,35	0,483	0,486	0,480
	контактная ф-я	0,03	0,03	0,25	0,575	0,575	0,574	-0,04	-0,09	-0,20	0,470	0,471	0,470
	активационная ф-я	-0,33	-0,33	-0,30	0,577	0,571	0,579	-0,28	-0,27	-0,30	0,476	0,472	0,478
	суггестивная ф-я	-0,85	-0,92	-1,05	0,459	0,451	0,461	-0,71	-0,73	-0,70	0,451	0,450	0,451
	мобилизационная ф-я	-1,29	-1,33	-1,30	0,377	0,358	0,383	-1,42	-1,44	-1,45	0,361	0,357	0,362

Табл.9. Таблица-напоминание о расстановке и названиях позиций соционических функций внутри ТИМа – на примере конкретного ТИМа ИЛЭ

программная	ЧИ (1)	БЛ (2)	творческая
мобилизационная	БЭ (4)	ЧС (3)	контактная
активационная	ЧЭ (6)	БС (5)	суггестивная
контролирующая	БИ (7)	ЧЛ (8)	демонстрационная

Рассмотрение диаграмм от рис.22. до рис.25. показывает, во-первых, что «плато» (сравнительно сглаженный плоский участок в форме кривой распределения) на рис.23. образуется за счет сложения распределений функций, находящихся в восьми различных позициях (см. рис.22.1.-22.8.). За счет этого же сложения образуется полимодальная структура (заметная «ухабистость) в форме кривой распределения на рис. 23 (особенно выраженная для мужской выборки на рис.23.1.). Полимодальная «ухабистость» на рис. 23 и рис.25., однако, изрядно сглажена, размыта – и причиной этому весьма широкие распределения величины функции в любой из ее конкретных позиций. Полуширина распределения (стандартное отклонение, «стандотклон») находится в диапазоне от 0,35 для программной функции до 0,57 для контактной, активационной и контролирующей функций, то есть функций средней величины. При этом надо учитывать, что, в действительности, это различие между полушириной распределения для функций в разных ее позициях внутри ТИМа является, скорее всего, расчетным артефактом. Дело в том, что для построения диаграмм использованы значения функций испытуемых в их уже отнормированных функциональных профилях. А при математическом нормировании профилей (операция приведения к единичному стандартному отклонению сначала тимного, а затем и функционального профиля каждого индивида) с максимальным весом учитываются функции, наиболее сильно отклоняющиеся от среднего нуля. После нормирования разброс этих функций по величине искусственно уменьшается. А это – как раз функции, находящиеся в самой сильной позиции (программная) и в самой слабой позиции (мобилизационная). Именно для этих функций разброс их величины между испытуемыми несколько снижается, по итогам нормирования, по сравнению с реальным, в то время как для функций, мало отличающихся от нуля – напротив, чуть возрастает. Поэтому правильнее говорить о предполагаемой единой полуширине распределения для функции в любых ее позициях внутри ТИМа, и верной оценкой этой полуширины будет усреднение стандартных отклонений, вычисленных для всех позиций функции. В итоге оказывается, что полуширина распределения (стандартное отклонение) соционической функции в любой ее конкретной позиции внутри ТИМа равна примерно 0,47, и это для любого конкретного положения функции внутри ТИМа (программного, творческого и т.д.) есть истинное значение популяционного разброса. Получается, что даже при фиксации вполне определенной позиции функции внутри ТИМа (например, творческой позиции) вариабельность величины функции остается весьма значительной (такой, что 34%, или 1/3 всех популяционных случаев даже остается за пределами полосы плюс-минус 0,47, откладываемых в обе стороны от среднего значения функции в ее рассматриваемой позиции). Эта значительная вариабельность свидетельствует, очевидно, о возможности очень значительных акцентуаций внутри ТИМа (когда для конкретных индивидов значения 8-ми функций внутри ТИМа значительно «пляшут», сильно отклоняясь от предписанных им и закрепленных за позициями функций средних популяционных значений).

Популяционное распределение разностей между величинами соционических функций внутри ТИМа в их определенных позициях. Функции рассчитаны по типным профилям, составленным из диагностических корреляций, нормированных по 1-му способу (к единичному стандартному отклонению нагрузок типного профиля). Все функциональные профили (индивидуальные наборы 8-ми функций в ТИМе испытуемых) перед построением диаграмм дополнительно нормализованы (делением на стандартное отклонение функционального профиля) вплоть до приведения всех функциональных профилей к единичному стандартному отклонению.

Рис.26.1. Распределение разностей величин программной и творческой функций индивида в смешанной экспериментальной выборке. Функции рассчитаны на основе типных профилей из диагностических корреляций, окончательные функциональные профили восьми функций внутри ТИМа нормированы для каждого испытуемого к единичному стандартному отклонению в разбросе его восьми функций по величине.

Рис.26.2. Распределение разностей величин программной и контактной функций индивида в смешанной экспериментальной выборке. Функции рассчитаны на основе типных профилей из диагностических корреляций, окончательные функциональные профили восьми функций внутри ТИМа нормированы для каждого испытуемого к единичному стандартному отклонению в разбросе его восьми функций по величине.

Рис.26.3. Распределение разностей величин творческой и контактной функций индивида в смешанной экспериментальной выборке. Функции рассчитаны на основе типных профилей из диагностических корреляций, окончательные функциональные профили восьми функций внутри ТИМа нормированы для каждого испытуемого к единичному стандартному отклонению в разбросе его восьми функций по величине.

Рис.26.4. Распределение разностей величин творческой и мобилизационной функций индивида в смешанной экспериментальной выборке. Функции рассчитаны на основе типных профилей из диагностических корреляций, окончательные функциональные профили восьми функций внутри ТИМа нормированы для каждого испытуемого к единичному стандартному отклонению в разбросе его восьми функций по величине.

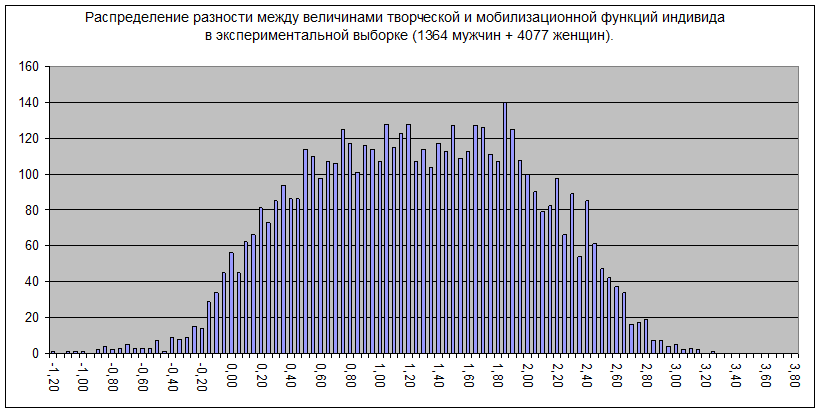
Рис.26.5. Распределение разностей величин контактной и мобилизационной функций индивида в смешанной экспериментальной выборке. Функции рассчитаны на основе типных профилей из диагностических корреляций, окончательные функциональные профили восьми функций внутри ТИМа нормированы для каждого испытуемого к единичному стандартному отклонению в разбросе его восьми функций по величине.

Рис.26.6. Распределение разностей величин программной и мобилизационной функций индивида в смешанной экспериментальной выборке. Функции рассчитаны на основе типных профилей из диагностических корреляций, окончательные функциональные профили восьми функций внутри ТИМа нормированы для каждого испытуемого к единичному стандартному отклонению в разбросе его восьми функций по величине.

Рис.26.7. Распределение разностей величин программной и демонстрационной функций индивида в смешанной экспериментальной выборке. Функции рассчитаны на основе типных профилей из диагностических корреляций, окончательные функциональные профили восьми функций внутри ТИМа нормированы для каждого испытуемого к единичному стандартному отклонению в разбросе его восьми функций по величине.

Рис.26.8. Распределение разностей величин демонстрационной и контролирующей функций индивида в смешанной экспериментальной выборке. Функции рассчитаны на основе типных профилей из диагностических корреляций, окончательные функциональные профили восьми функций внутри ТИМа нормированы для каждого испытуемого к единичному стандартному отклонению в разбросе его восьми функций по величине.

В среднем по восьми выше приведенным разностям функций полуширина распределения разности (стандартное отклонение популяционного распределения разности двух функций) составляет 0,745. Очевидно, что это - значительная величина, указывающая на очень большую свободу в формировании акцентуаций в пределах психотипа. Напомним также, что полуширина распределения величины каждой функции в отдельности составляет в среднем 0,47.

Выводы:

1) Возможные акцентуации типа имеют конечный фиксированный «радиус» в метрике нормированных диагностических корреляций (см. Полуширину популяционного распределения разности нормированных диагностических корреляций, столбики 3 и 4 в табл.3.). Таким образом, возможный эффективный радиус акцентуации постоянен и не зависит от того, в направлении какого типа (квазитождика, родственника, конфликтера, и т.п.) акцентуация осуществляется. В том случае, если расстояние между типами (столбики 1 и 2 в табл.3.) более чем в три раза превосходит этот фиксированный радиус, зона границы между типами становится пустой, практически свободной от людей. Если же расстояние между типами в метрике диагностических корреляций меньше трехкратного радиуса возможной акцентуации типа, то граница между типами оказывается не пустой, находятся люди, которые со своими акцентуациями попадают даже непосредственно на эту границу. Их тем больше, чем меньше отношение расстояния между типами к константному радиусу акцентуаций.

2) 16 соционических типов в метрике диагностических корреляций разделены между собой естественными границами. Хотя при небольшом расстоянии между типами акцентуации и могут «заползать» даже непосредственно на эту границу, но граница между типами от этого не теряет свою объективность, так как на ней плотность людей, попадающих благодаря своим акцентуациям в эту граничную зону, все равно минимальна, она в несколько раз меньше плотности людей, заполняющих «сердцевину» типа.

3) Наиболее «размыта» граница между квазитождественными типами – благодаря их близости друг к другу в метрике диагностических корреляций. Наиболее четко выражена (и даже имеет широкую «запретную полосу») граница между типами-конфликтерами – благодаря их значительной удаленности друг от друга в метрике диагностических корреляций.

4) Обособленное существование 16-ти соционических типов тем не менее нельзя считать, благодаря результатам настоящего исследования, вполне подтвержденным. Оно подтверждено лишь в метрике диагностических корреляций, однако сами эти корреляции являются с математической точки зрения локально настроенными на определенные участки психологического пространства широкополосными фильтрами, пропускание этих фильтров (и величина наблюдаемой корреляции) довольно быстро спадают по мере удаления от точки настройки, поэтому нельзя вполне исключать того, что получающиеся «объективные» границы между типами являются лишь артефактом методики математических расчетов.

5) Для окончательных выводов об обособленности либо необособленности соционических типов необходимо провести расчеты в метрике непрерывных диагностических шкал, а не коэффициентов корреляций. Что такое непрерывная диагностическая шкала и как ее использовать, например, для изучения перехода между ЛИИ и ИЛИ? Для ЛИИ в анкете выбираются те вопросы, на которые именно этот тип дает максимальные ответы. То же – для типа ИЛИ. Положительные ответы на свой для каждого типа набор эксклюзивных вопросов суммируются с необходимыми весовыми коэффициентами, зависящими в свою очередь от меры эксклюзивности этих вопросов для типа. Это и есть непрерывные диагностические шкалы, создаваемые отдельно для каждого из 16-ти типов. Сами типы – ЛИИ и ИЛИ в том числе – диагностируются у испытуемых, впрочем, обычным наиболее точным методом, с помощью процедуры диагностических корреляций. Суммы ответов по шкалам нормируются до единичного стандартного отклонения – каждая на массиве ответов представителей только «своего» типа. Далее соответствующие суммы вычисляются уже для всех испытуемых выборки. После этого на массиве испытуемых-ЛИИ можно сравнить между собою результаты непрерывных диагностических шкал для измерения выраженности свойств ЛИИ и ИЛИ, аналогично поступить для массива испытуемых-ИЛИ, и затем по распределению величины разности между результатами двух диагностических шкал анализировать в массиве именно представителей этих двух психотипов – ЛИИ и ИЛИ – пограничную зону между ними. Плюс такого подхода состоит в том, что непрерывные диагностические шкалы, в отличие от коэффициентов корреляции, не имеют локальной настройки на определенную зону психологического пространства и, более того, имеют линейную математическую природу.

6) Результаты, полученные в части 3 настоящей статьи, указывают на возможность очень значительного варьирования соционических функций внутри ТИМа по их относительной друг к другу величине, что подтверждает наличие в популяции значительных соционических акцентуаций, соответствующих усилению или ослаблению каких-то функций внутри ТИМа. С другой стороны, распределение величины всех функций внутри ТИМа имеет в популяции фактуру, близкую к зубчатой полимодальной, то есть популяционное колебание величины функций возле их средних зависящих от позиции значений все же ограничено.

7) В метрике диагностических корреляций нерезко выраженная бимодальность обнаруживается только для полюсов соционических признаков экстраверты-интроверты, интуиты-сенсорики и логики-этики, для прочих признаков бимодальность не обнаружена даже в метрике жиагностических корреляций. Для окончательных выводов о наличии или отсутствии бимодальности в физиологическом распределении вертности, логики-этики и интуиции-сенсорики необходимо, как и в случае исследования границ между типами, применение непрерывных диагностических шкал.

Ссылки:

В.Л.Таланов. Полные психологические портреты психотипов (маркерные характеристические свойства) на основе результатов экспериментального исследования:

1. ИЛЭ - http://sociotoday.narod2.ru/ILE.html

2. ЛИИ - http://sociotoday.narod2.ru/LII.html

3. ИЛИ - http://sociotoday.narod2.ru/ILI.html

4. ЛИЭ - http://sociotoday.narod2.ru/LIE.html

5. СЛЭ - http://sociotoday.narod2.ru/SLE.html

6. ЛСИ - http://sociotoday.narod2.ru/LSI.html

7. СЛИ - http://sociotoday.narod2.ru/SLI.html

8. ЛСЭ - http://sociotoday.narod2.ru/LSE.html

9. ИЭЭ - http://sociotoday.narod2.ru/IEE.html

10. ЭИИ - http://sociotoday.narod2.ru/EII.html

11. ИЭИ - http://sociotoday.narod2.ru/IEI.html

12. ЭИЭ - http://sociotoday.narod2.ru/EIE.html

13. СЭЭ - http://sociotoday.narod2.ru/SEE.html

14. ЭСИ - http://sociotoday.narod2.ru/ESI.html

15. СЭИ - http://sociotoday.narod2.ru/SEI.html

16. ЭСЭ - http://sociotoday.narod2.ru/ESE.html

17. В.Л.Таланов. Всё неизвестное и малоизвестное о восьми функциях психики. Часть I: Расчёт функций, количественное значение всех функций в психотипе, содержательное наполнение функций - http://sociotoday.narod2.ru/funkcii1.html

Дополнительная литература:

1. В.Л.Таланов. Примеры исторических знаменитостей из числа всех 16 психотипов (900 персоналий с комментариями) - http://sociotoday.narod2.ru/tabl.html

2. Другие статьи В.Л.Таланова с 2011 года - http://sociotoday.narod2.ru/index1.html

3. Работы В.Л.Таланова о психофизиологической модели ТИМа (модель «Т»), а также о психофизиологических и психологических интерпретациях признака «интуиция-сенсорика» - http://www.newsocionicsmodel.narod.ru/

Статья впервые опубликована 24.04.2012 в http://sociotoday.narod2.ru/granicy_tipov1.mht

Воспроизведение статьи допускается только с разрешения автора. Цитирование – свободно (со ссылкой).

Оставить отзыв можно по адресу: ГОСТЕВАЯ КНИГА

Написать автору -

⇐ Предыдущая 1 2 3 4 5 67

Воспользуйтесь поиском по сайту: