Лекция № 2. Основы технической термодинамики идеальных газов

 

Техническая термодинамика это наука, занимающаяся изучением законов превращения энергии в тепловых машинах. Наука базируется на некоторых экспериментально установленных фактах или законах и оперирует определенными терминами.

Термодинамическая система является объектом исследования в термодинамике и представляет собой некую выделенную исследователем область пространства, в которой располагается некоторое количество вещества. Термодинамическая система отделяется от окружающей среды материальной или воображаемой мнимой оболочкой, которая называется границей системы. Можно для примера представить цилиндр поршневой машины с находящимся внутри газом, который назовем рабочим телом. Если система обменивается веществом с окружающей средой, то она называется открытойтермодинамической системой, если обмен невозможен, то такая система называется закрытой термодинамической системой. Если система не имеет возможности никакого взаимодействия с окружающей средой, то такая термодинамическая система называется изолированной термодинамической системой

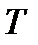Термодинамические параметры системы -это величины, характеризующие состояние термодинамической системы (по другому, их называют параметрами состояния). Параметры состояния можно определить доступными средствами и приборами методом прямых измерений. К параметрам состояния относят: абсолютное давление, = [Па] = [Н/м²]; масса, = [кг]; объем, = [м³]; температура, = [К]. Бывает удобно соотносить объем к единице массы и тогда используется величина – удельный объем = [м³/кг]. Для отправной точки расчетов и для приведения параметров при сравнении вводятся нормальные условия, которыми принято считать 273,15 К и 0,101325 МПа (0 ^оС и 760 мм рт.ст.).

При неизменных внешних условиях – условий окружающей среды, термодинамическая система в конечном итоге приходит в определенное установившееся состояние, которое называют равновесным. Равновесное состояние термодинамической системы характеризуется неизменностью во времени всех параметров и отсутствием в системе потоков вещества и теплоты. Для такой системы существует определенная зависимость параметров состояния. Эта математическая зависимость называется законом Клапейрона или уравнением состояния идеального газа и может быть записана как:

Или, если воспользоваться удельным объемом, то уравнение состояния примет вид:

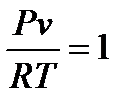
Где - коэффициент, который называется газовой постоянной. Газовая постоянная зависит только от природы газа и независима от параметров состояния.

Газы, подчиняющиеся этому уравнению, называются идеальными. Нужно отметить, что идеальными газами можно считать многие газы в достаточно широком диапазоне температур (до 1500-2000К) и давлений (до 10-12 МПа) и, следовательно, использовать для приблизительных расчетов уравнение Клапейрона.

Если мы условно выделим объем газа, в котором будет присутствовать такое число структурных единиц – молекул, сколько содержится атомов в 12 г изотопа углерода-12, а именно 6,022х 10(23) (а эта величина называется постоянной Авогадро), то такое количество вещества называется молем. Тогда, если газовую постоянную отнести к одному молю вещества, получится постоянная величина, называемая универсальной газовой постоянной. Известно, что один киломоль газа при нормальных условиях занимает строго определенный объем, а именно – 22,41383 м³/кМоль. Следовательно, универсальная газовая постоянная может быть вычислена подстановкой численных значений параметров нормальных условий в видоизмененное уравнение состояния идеального газа:

Где – молярная масса (в кг/Моль), равная отношению массы газа к количеству вещества

Исходя из этого, параметры уравнения состояния идеального газа можно вычислять и по формуле:

Любое изменение состояния термодинамической системы характеризуется изменением термодинамических параметров системы и называется термодинамическим процессом. Если термодинамический процесс можно рассматривать как непрерывный ряд равновесных состояний системы, то процесс называют равновесным. Если при совершении термодинамического процесса в прямом и обратном направлении, термодинамическая система и окружающая среда возвращаются в начальное (исходное) состояние, то такой процесс называют обратимым термодинамическим процессом.

Процесс совершается, когда система отдает часть своей энергии окружающей среде или получает от нее энергию, а также при переносе вещества от системы к окружающей среде и наоборот.

Из формулы 1.1. следует, что:

Тогда мы в праве рассмотреть частные случаи термодинамических процессов, которые имеют определенные названия и сведены в табл. 2.1.

 

Таблица 2.1

Термодинамические процессы

 

процесс	изобарический	изохорический	изотермический
признак	= const	= const	= const
формула
Имя	Гей-Люсака		Бойля-Мариотта

 

В дальнейшем мы произведем визуализацию поименованных процессов.

Как следует из наших размышлений, к термодинамической системе может подводиться (или отводиться от нее) энергия в двух видах: работы и теплоты.

Работа термодинамического процесса это количественная характеристика формы передачи энергии через границы термодинамической системы, не зависящая от температур системы и окружающей среды и не связанная с переносом вещества от системы к окружающей среде и обратно. Для произвольного равновесного процесса 1-2 работа в Дж определяется выражением:

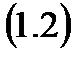
Участвующее в термодинамическом процессе вещество, посредством которого осуществляется преобразование теплоты в работу и обратно называется рабочим телом. Работу процесса, отнесенную к массе рабочего тела, называют удельной работой. Она обозначается в Дж/кг и определяется формулой:

Из формул (1.2) и (1.3) следует, что при увеличении объема системы, работа процесса положительна или энергия, отводимая от системы в виде работы в окружающую среду, считается положительной.

Теплота процесса – это количественная характеристика формы передачи энергии через границы термодинамической системы, зависящая только от разности температур системы и окружающей среды и не связанная с переносом вещества между ними. Для произвольного равновесного процесса 1-2 теплота в Дж определяется выражением

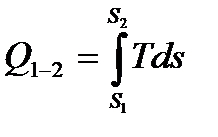
где S₂, S₁, S - конечная начальная и текущая энтропия системы в Дж/К.

Отнесенная к массе рабочего тела теплота, называется удельной и обозначается в Дж/кг.

Энтропией называется физическая величина, изменение которой в обратимых процессах является признаком наличия обмена энергией в форме теплоты. Значение энтропии определяется состоянием системы, т.е. энтропия – функция состояния. Увеличение энтропии термодинамической системы происходит при подводе к ней теплоты.

Очевидно, что значения термодинамической работы и теплоты процесса зависят от вида самого процесса, совершаемого системой. Поэтому дифференциалы работы и теплоты не являются полными и мы будем их обозначать и , а сами величины называются функциями процесса.

Если мы к нашей термодинамической системе в некотором процессе подведем элементарное количество теплоты , то получим бесконечно малое изменение температуры вещества . Тогда отношение элементарного количества теплоты, полученного веществом при бесконечно малом изменении его состояния в каком либо процессе, к соответствующему бесконечно малому изменению температуры вещества, называют истиннойтеплоемкостью, Дж/к.

Теплоемкость, отнесенная к массе вещества, называется удельной массовой теплоемкостью (обозначается в Дж/кг К), а к количеству вещества – удельной молярной теплоемкостью (обозначается в Дж/моль К). В расчетах чаще используется удельная массовая теплоемкость, которую будем в дальнейшем называть просто удельной теплоемкостью.

У идеального газа теплоемкость зависит от температуры, Поэтому для упрощения расчетов вводится средняя удельная теплоемкость:

Для себя отметим, что теплоемкость идеального газа в принципе зависит от процесса, в котором подводится энергия, но об этом поговори немного позже, а сейчас отвлечемся и рассмотрим смеси газов.

Хорошо если наша рассматриваемая термодинамическая система заполнена одним газом, который мы рассматриваем как идеальный, тогда все просто. А как быть, если в рассматриваемой системе находится смесь газов. Такая ситуация в технике в тепловых машинах встречается постоянно. Как, в частности, определить газовую постоянную. Рассмотрим некую произвольную смесь газов. Каждый газ, входящий в состав смеси называют компонентом смеси. Каждый компонент смеси, заполняя полный объем, занимаемый всей смесью, будет иметь свое определенное давление _, которое называется парциальным давлением компонента. Если компоненты смеси рассматриваются как идеальные газы, то в соответствии с законом Дальтона, давление, под которым находится смесь, равняется сумме парциальных давлений всех компонентов данной смеси. Таким образом,

Содержание самих компонентов в смеси обычно выражают в долях – массовых, объемных и молярных. Сумма долей, как очевидно, равна единице. Определим отношение массы -го компонента смеси ко всей массе смеси как массовую долю -го компонента. То есть:

Если мы условно выделим массу -го компонента и поместим его под давление смеси, то он займет определенный объем , который называется парциальным объемом. Тогда объемной долей компонента в смеси газов назовем отношение парциального объема -го компонента к объему смеси:

И, наконец, молярной долей y_i i-го компонента называют отношение количество вещества данного компонента к общему количеству вещества смеси, то есть:

Но количество вещества 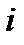-го компонента, по определению, есть отношение массы -го компонента к молярной массе этого элемента, и оно же равно отношению парциального объема этого компонента к объему одного моля:

При этом, как мы уже рассмотрели ранее, объем одного моля идеального газа при одинаковых условиях для всех газов постоянен:

В расчетах смесь идеальных газов принимают за условный идеальный газ со своей газовой постоянной , молярной массой и др. характеристиками. Условный газ имеет такую же массу и количество молекул, как и смесь, но состоит из одинаковых по массе молекул. Запишем уравнение состояния для -го компонента и, просуммировав, их получим:

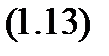
но, как мы уже условились, можно сказать и так:

Тогда понятно, что:

Теперь вернемся после отвлечения к рассмотрению функций состояния термодинамической системы. Но прежде сформулируем Первый закон термодинамики. Формулировок закона сохранения энергии для термодинамики, а именно о сохранении энергии гласит первый закон термодинамики много. Скажем так: во всех тех случаях, когда исчезает некоторое количество тепловой энергии, возникает вполне определенное количество механической энергии (работы) и, наоборот, при совершении какой либо работы появляется вполне определенное количество тепловой энергии. Таким образом, невозможно сконструировать такой двигатель, который вырабатывал бы энергию <из ничего>, не потребляя какой либо энергии, например, энергии сгорания топлива. Такой двигатель получил название вечный двигатель (перпетум мобиле) первого рода. А, следовательно, еще одна, самая запоминающая формулировка Первой Основы термодинамики гласит: перпетум мобиле первого рода не возможен.

Исходя из первого закона термодинамики, рассмотрим закрытую термодинамическую систему, в которой в равновесном процессе 1-2 подводится работа. По закону сохранения энергии, подведенная работа не может исчезнуть бесследно, а должна аккумулироваться в системе в виде изменения внутренней энергии системы:

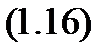
Знак минус в уравнении (1.16) учитывает то, что подводимая работа отрицательна. Уравнение (1.16) справедливо и при положительной работе, так как при совершении работы системой, расходуется внутренняя энергия системы.

Внутренняя энергия представляет собой сумму кинетических и потенциальных энергий структурных единиц рассматриваемого вещества (молекул, атомов, ионов). Часть внутренней энергии вещества может изменяться за счет протекания химических превращений и должна учитываться только в процессах, сопровождаемых химическими реакциями. Понятно, что значение внутренней энергии определяется состоянием системы, то есть 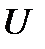– есть еще одна функция состояния. В математическом отношении это означает, что элементарное приращение внутренней энергии является полным дифференциалом и, следовательно:

 

Аналогичные уравнения справедливы для всех функций состояния. В общем случае, когда система обменивается с окружающей средой теплотой и работой, уравнение баланса энергий, или уравнение первого закона термодинамики имеет вид

Разделив все члены уравнения (1.18) на массу рабочего тела получаем:

Уравнения (1.18) и (1.19) показывают, что изменение внутренней энергии системы равно сумме энергии, полученной системой в форме теплоты и работы. Или, по иному, количество теплоты, подведенное в систему, в общем случае, расходуется на совершение работы и увеличение внутренней энергии системы.

Так как в изохорном процессе работа не совершается, то с учетом определения теплоемкости из выражения (1.5), для изохорного процесса запишем (1.19) как

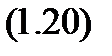
Но ведь формула (1.20) справедлива для любого процесса, поскольку внутренняя энергия есть функция состояния. Тогда для изобарного процесса уравнение (1.19) с учетом (1.3) и (1.5) принимает вид:

Или

Индекс у производной показывает, что она взята при постоянном давлении.

Из уравнения Клапейрона имеем для изобары:

Теперь подставим это выражение в (1.21) получаем взаимозависимость удельных теплоемкостей в изохорном и изобарном процессе, известную, как уравнение Майера.

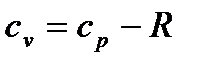
Применим совершенно искусственный прием, а именно, прибавим и сразу же отнимем от правой части уравнения (1.19) выражение . Тогда после ряда математических преобразований запишем:

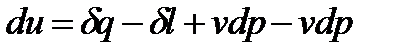
Теперь выражение, находящееся в левой части уравнения, выделим в отдельную новую функцию состояния и назовем ее удельной энтальпией

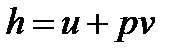
Тогда получаем еще один вид записи уравнения первого закона термодинамики:

Продифференцировав выражение (1.23), получим

Откуда, использовав, формулы (1.1), (1.20) и (1.22) выведем уравнение, используемое для расчета удельной энтальпии.

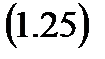
Второе слагаемое в выражении (1.24) называется элементарной удельной технической работой и обозначается как:

А из этого определения получаем выражение для расчета технической работы:

В отличие от работы процесса, техническая работа представляет собой сумму работы процесса с работой по равновесному (изобарному) вводу рабочего тела в систему и его вывода. Необходимость введения знака минус в формулах (1.26) и (1.27) объясняется тем, что для сжатия рабочего тела (а при этом dp больше нуля) работу к системе нужно подвести, а, следовательно, должна быть отрицательной.

Сейчас рассмотрим самый общий случай протекания обратимого термодинамического процесса, назвав его политропный (процесс, идущий в разных направлениях). Для этого, используя формулы (1.3), (1.5), (1.20) и (1.25), запишем уравнения первого закона термодинамики (1.19) и (1.24) в виде:

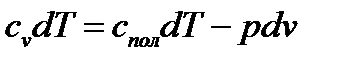
После почленного деления и преобразований получаем уравнение политропного процесса в дифференциальной форме:

или

Где – показатель политропы

Если использовать среднее значение теплоемкости, то показатель политропы будет постоянной величиной и уравнение (1.28) после интегрирования получает вид

Это равенство называется уравнением политропы. Из этой зависимости, как частные случаи, можно получить все известные процессы. Так если процесс идет без подвода теплоты, то, по определению, и, следовательно, становится равным

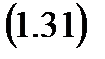
Такой процесс называется адиабатным, а – показателем адиабаты. Тогда уместно записать

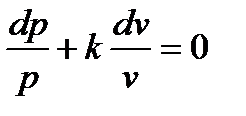
и

Уравнение (1.33) называют уравнением адиабаты.

Далее, если = 1, то, как очевидно, мы получаем известный нам изотермический процесс. Если = 0, тогда процесс изобарный, ну а если становится бесконечным, то получаем изохорный процесс.

 

Из уравнения (1.28) находим соотношение между удельными работами (процесса и технической).

Что касается самой работы процесса, то можно рассмотреть для простоты адиабатный процесс. В адиабатном процессе или . Умножим и разделим правую часть на , а так как это выражение ни что иное как , получаем:

или

По аналогии, для политропного процесса, выражение для расчета работы процесса будет:

или

Теплота, подведенная к системе в политропном процессе, может быть определена из уравнений (1.5) и (1.6), а теплоемкость получится, если преобразовать выражение (1.29) и тогда она, примет вид:

Изменение удельной энтропии процесса можно вывести из уравнения первой основы термодинамики:

но одновременно:

или

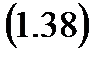
В то же время, из (1.24):

то есть:

или

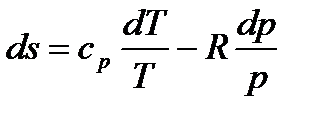
Рассматривая диаграммы и , отметим, что адиабата в

 

Рис. 2.1. Отображение термодинамических процессов

 

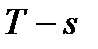диаграмме идет круче изотермы (рис. 2.1), т.к., в отличии от изотермы , у адиабаты зависимость степенная , а больше единицы. В диаграмме изохора идет круче изобары из за разности в теплоемкостях процессов: больше, чем . Или в изохорном процессе не совершается работа, поэтому подвод тепла связан с ускоренным ростом температуры, в отличие от изобары, где подведенная теплота расходуется и на совершение работы.

Проведем рассмотрение термодинамических циклов. А для этого рассмотрим некую последовательность процессов, после совершения которых рабочее тело нашей системы приходит в исходное состояние и назовем такой круговой процесс циклом. Если все процессы, составляющие цикл являются обратимыми, то такой цикл будем называть обратимым. Принято считать, что в тепловых двигателях рабочее тело совершает прямой цикл (по часовой стрелке) а в холодильных машинах и в тепловых насосах – обратный (против часовой стрелки). В прямых циклах часть подведенной к рабочему телу теплоты преобразуется в работу, а часть отводится в окружающую среду. В обратных же циклах, теплота переходит от тела с меньшей температурой к телу с большей температурой за счет затраты энергии.

Для иллюстрации дальнейших рассуждений, на рис. 2.2 приведены в самой общей форме прямой и обратный циклы в диаграмме.

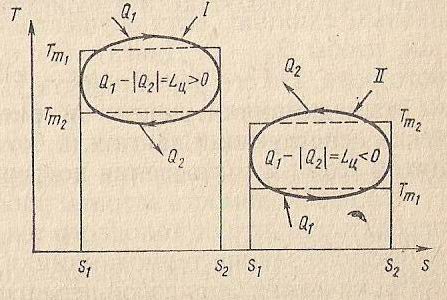
Рис. 2.2. Термодинамические циклы

 

Уравнение первого закона термодинамики для цикла имеет вид:

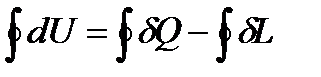
А так как интеграл по в круговом цикле равен нулю, то, воспользовавшись формулами для работы и тепла, имеем:

Или

Для оценки эффективности цикла теплового двигателя вводят понятие термического коэффициента полезного действия (КПД), который представляет собой отношение работы цикла к подведенной теплоте:

Эффективность обратного цикла, реализуемого в холодильной машине, оценивается холодильным коэффициентом – отношением теплоты, отведенной от охлаждаемого объекта к затраченной при этом работе:

Коэффициент теплоиспользования, представляющий собой отношение теплоты Q₂ , отдаваемой нагреваемому объекту к абсолютной величине работы цикла Lц характеризует эффективность обратного цикла, реализуемого в тепловом насосе.

На основании теоремы о среднем значении определенного интеграла запишем:

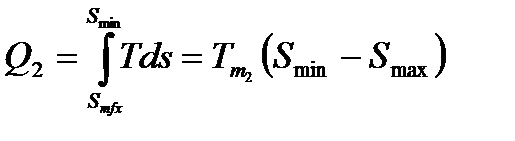
Тогда для термического кпд цикла справедливо:

Обратимый цикл из двух адиабат и двух изотерм получил название цикла Карно. И, как следует и 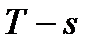диаграммы, имеет максимальный кпд при заданных температурах подвода и отвода тепла. В цикле Карно температуры и становятся равными и изотермического расширения и сжатия. Поэтому КПД цикла Карно:

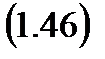
Из формулы (1.41) очевидно, что для того, чтобы кпд теплового двигателя стал равен единице, цикл нужно осуществлять без отвода теплоты, когда равно нулю. Двигатель с термическим КПД равным единице назван вечным двигателем (перпетум мобиле) второго рода. Вторая основа термодинамики гласит, что невозможно создать вечный двигатель второго рода. Этот факт, установленный путем длительных наблюдений и размышлений человечества над сущностью тепловых двигателей требует разъяснений. В принципе первый закон термодинамики не отрицает возможности превращения тепловой энергии в механическую в каком либо процессе полностью, как закон сохранения энергии, как таковой. Но мы рассматриваем круговой процесс (цикл) теплового двигателя, который совершается периодически или циклически. Причем этот циклически работающий двигатель может совершать любое количество таких круговых процессов так долго, как это нужно. При этом обязательным условием циклической работы такого двигателя будет периодическое непременное возвращение каким то образом рабочего тела к первоначальным исходным параметрам рассматриваемой термодинамической системы за счет отвода некоторого количества тепла, полученного от горячего источника тепла к холодному источнику. Иная формулировка Второй основы термодинамики была предложена в 1852 г Планком, согласно которой: Невозможно построить периодически действующий двигатель, который производил бы только поднятие груза и охлаждение источника тепла.

С другой стороны, тепловой двигатель, который имеет термический КПД, равный единице, как следует из формулы (1.45) должен иметь температуру изотермы отвода тепла ноль Кельвинов. Но при 0 К теряет смысл, в частности, понятие теплоемкости так как прекращается всякое тепловое движение. И в этом случае теплоемкость равна О. То есть для реализации цикла с термическим кпд, приближающемся к единице за счет приближения температуры теплоприемника к 0, потребуется бесконечно большое количество рабочего тела.

В завершении изучения раздела термодинамики идеальных газов коснемся рассмотрения некоторых известных в технике циклов.

Представленный на рис. 2.3 цикл состоит из двух адиабат, изобары и изохоры. Этот цикл является термодинамической моделью процессов, происходящих в тепловом двигателе внутреннего сгорания. Цикл называют циклом Дизеля – по имени талантливого немецкого инженера Рудольфа Дизеля, изобретателя поршневого двигателя, работающего с самовоспламенением топлива в цилиндре.

Рис. 2.3. Цикл Дизеля

 

На рис 2.4 тоже показан цикл поршневого двигателя, в отличие от предыдущего, такой двигатель работает с принудительным воспламенением топливовоздушной смеси в цилиндре (искровой или бензиновый двигатель). Этот цикл двух адиабат и двух изотерм называют циклом Отто.

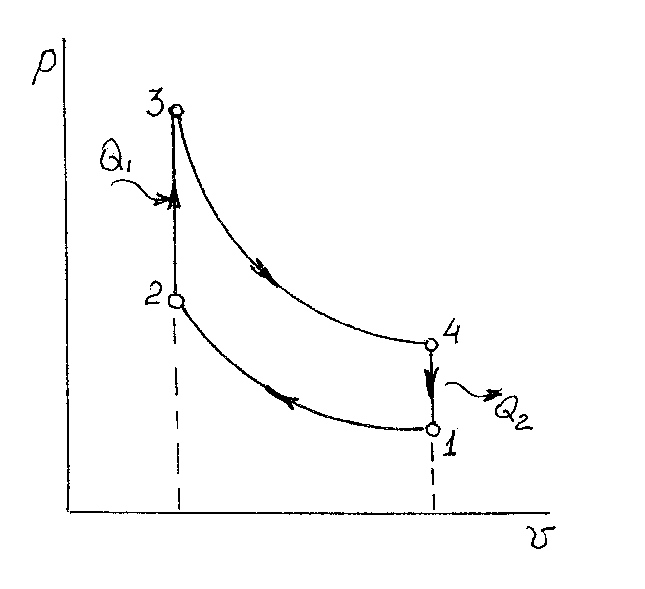
Рис.2.4. Цикл Отто

 

Все современные дизельные двигатели работают по циклу со смешанным подводом тепла. Подвод тепла в таком цикле происходит в двух процессах – изохорном и изобарном, а отвод тепла – в изохорном, как и во всех выше рассмотренных циклах. Диаграмма цикла приведена на рис. 2.5.

 

 

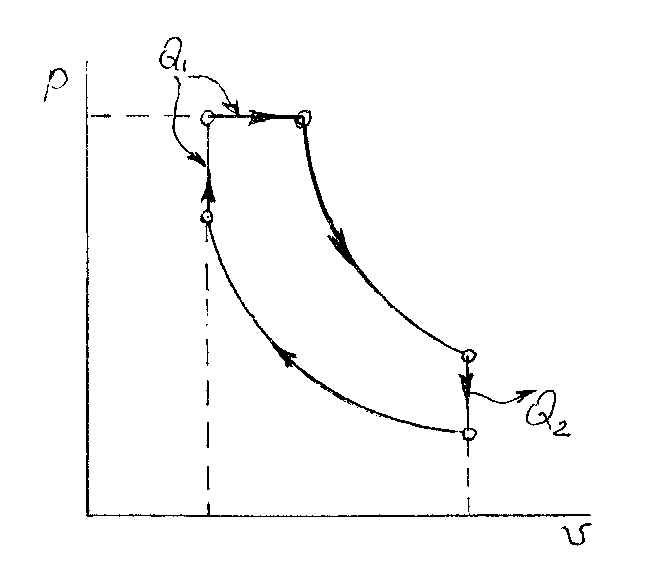
Рис 2.5. Цикл со смешанным подводом тепла

В отличие от всех вышеперечисленных циклов поршневых двигателей, идеальный цикл газотурбинной установки, представленный на рис. 2.6., производит отвод тепла в изобарном процессе. Действительно, в то время как в поршневом двигателе перезарядка цилиндра свежим зарядом происходит условно при одном и том же объеме, в газотурбинной установке, процесс отвода отработавшего рабочего тела идет постоянно и давление при этом остается неизменным. Подвод тепла в цикле ГТУ происходит по изобаре, а сжатие и расширение – по адиабате.

 

 

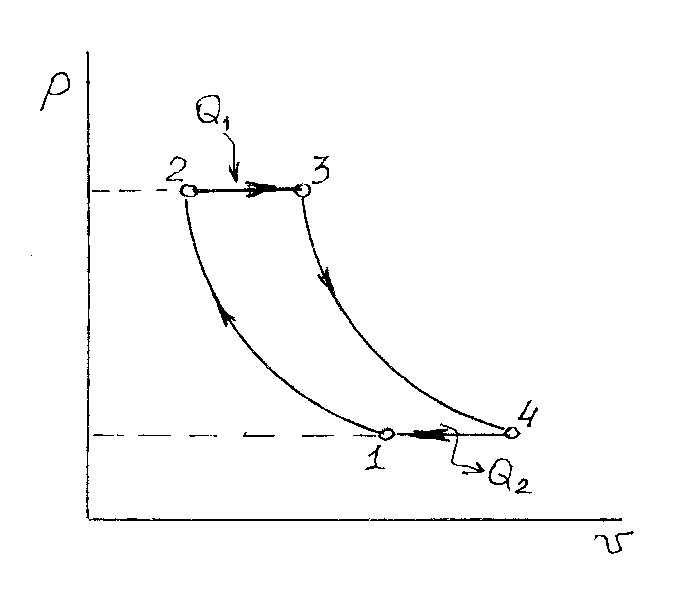
Рис 2.6. Цикл газовой турбины

 

Предложенный перечень известных циклов можно продолжать и далее. Рассматривая идеальные циклы, нельзя не упомянуть о цикле Ренкина (по которому работают паросиловые установки), цикле Стирлинга, цикле Карно и т.д.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: