Лекция №3. Реальные газы, водяной пар, влажный воздух, течение газов

 

Не всегда газ, даже с определенными допущениями, можно считать идеальным. Довольно часто в технике отклонения в характере поведения реальных газов от идеальных могут приводить к ощутимым ошибкам и расчеты давать недостоверные результаты.

Состояние реального газа описывается уравнениям состояния реальных газов, полученных экспериментальным путем. В общем случае:

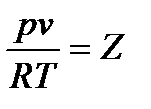
Строгого математического вывода коэффициента сжимаемости Z не существует. Поэтому в технике используют экспериментально полученные зависимости, например, Боголюбова, Новикова, Бертло и др. Нужно сказать, что эти уравнения достаточно достоверно описывают состояние определенных реальных газов в конкретных условиях, но они не универсальны.

Состояние реального газа достаточно хорошо, если не с количественной, то с качественной стороны характеризует уравнение Ван-дер-Ваальса, предложенное им в 1873 г.

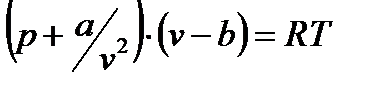
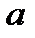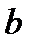Где и - постоянные для данного газа величины, причем 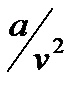– поправка, учитывающая силы сцепления между молекулами, а 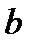– поправка, учитывающая объем самих молекул. Легко увидеть в этом уравнении знакомое уравнение Клапейрона. Очевидно, что уравнение Ван-дер-Ваальса – кубическое, а, следовательно, при определенных и 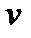оно имеет три корня. Получается кажущийся парадокс, а именно: если, корни уравнения не равны между собой и не мнимые, то при определенных температуре и давлении, вещество может иметь три различных объема. Однако это противоречие кажущееся. Два из трех различных значений объема соответствуют различным состояниям вещества: газообразному и жидкому, а третий объем – промежуточное значение, которое в опыте неосуществимо. Если три корня уравнения окажутся равными друг другу, то вещество находится в критическом состоянии, о котором поговорим далее. Если два корня уравнения – мнимые то это вещество – газ.

В качестве реального газа рассмотрим водяной пар. Представим закрытую термодинамическую систему, в объем которой залита вода. Молекулы жидкости, также как и молекулы газа, находятся в хаотическом движении. Если над жидкостью есть свободное пространство, то наиболее подвижные молекулы способны покинуть объем жидкости и перейти в свободное пространство над поверхностью раздела. При этом объем жидкости, естественно, будет уменьшаться. Такой процесс называется испарением. Какое-то количество испарившихся молекул возвращаются обратно в жидкость и, в какой-то момент времени, этот процесс придет в равновесие, т.е. количество молекул покинувших жидкость и вернувшихся в нее сравняется. Такое состояние называется насыщением, а образовавшийся пар – насыщенным. Таким образом, насыщенный пар находится в динамическом равновесии с жидкостью. Давление и плотность насыщенного пара при определенной температуре принимают совершенно конкретные значения.

Зависимость термодинамических параметров насыщенного пара совершенно иная, нежели у идеального газа. К примеру, если мы попытаемся при постоянной температуре уменьшить объем пространства, занимаемого насыщенным паром, то вопреки ожиданиям, давление его не изменится, а некоторая определенная часть молекул насыщенного пара перейдет в жидкость. В этом случае говорят, что пар конденсируется.

Рассмотрим, что будет происходить с жидкостью, помещенной в объем цилиндра с подвижным поршнем при изменении температуры при постоянном давлении. Отобразим этот процесс в диаграмме, рис. 3.1.

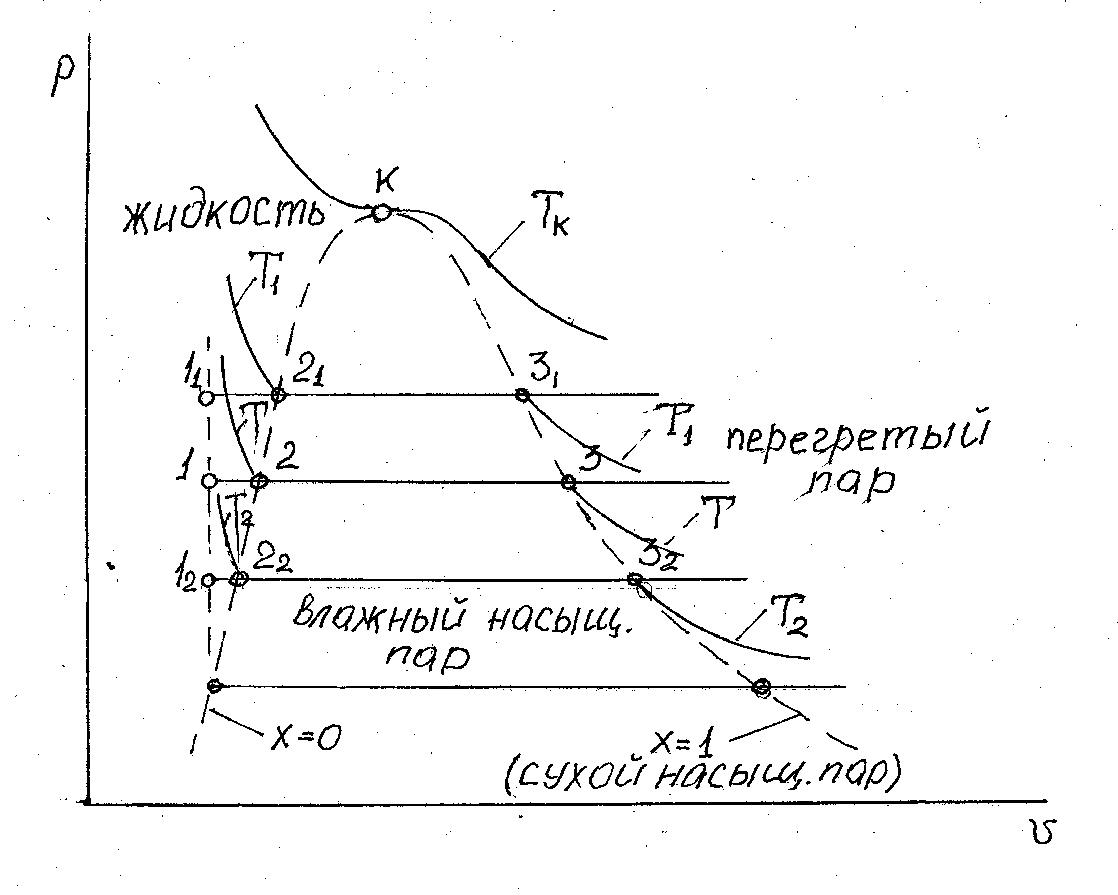
Рис. 3.1. Диаграмма фазового перехода

 

По мере подвода тепла и соответствующего повышения температуры при давлении 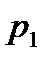, жидкость начнет увеличивать свой объем. Этот процесс будет происходить до определенной температуры, при которой давление насыщенного пара не сравняется с давлением (или, точнее, незначительно его превысит). При этих условиях в объеме жидкости возможно образование пузырьков насыщенного пара. Понятно, что при давлении насыщенного пара менее чем давление окружающей среды, образование таких объемов насыщенного пара в жидкости невозможно, т.к. они были бы моментально сжаты внешним давлением. Такое состояние жидкости с образованием насыщенного пара в ее объеме называется процессом кипения или просто кипением. Отобразим это на диаграмме точкой 2. По мере дальнейшего подвода тепла от точки 2 начинается образование пара из объема жидкости, при этом температура системы меняться не будет, а вся подведенная тепловая энергия будет затрачена на процесс образования насыщенного пара. Эта неизменная температура называется температурой кипения - 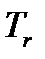. Обратим внимание, на то, что мы рассматриваем процесс при , т.е. температура кипения свойственна именно этому давлению при ином давлении эта температура будет другой. Таким образом, если между точками 1 и 2 мы имели жидкость, то после точки 2 наша система содержит две фазы – насыщенный пар и кипящую жидкость, причем жидкость может быть не только внизу цилиндра, но распылена по стенкам цилиндра. Такой насыщенный пар, содержащий в себе жидкость, называется влажным насыщенным паром. По мере дальнейшего подвода теплоты мы достигнем состояния системы, когда вся жидкость превратиться в пар. Обозначим эту точку – 3, а пар в этой точке назовем сухим насыщенным паром. За точкой 3 на диаграмме находится область перегретого пара. Перегретый пар, по своему поведению не отличим от обычного газа, а при определенных условиях, может рассматриваться как идеальный газ. А это значит, что при изобарном подводе тепла, с ростом будет увеличиваться температура перегретого пара. Если мы проведем серию опытов по нагреву цилиндра, заполненного водой, при разных давлениях, то получим семейство изобар с характерными точками 1_n, 2_n, 3_n. Объединив все точки 2n и 3n на поле наших характеристик, мы получаем пограничные кривые - границы разделов, где существует жидкость, влажный насыщенный пар и перегретый пар. Введем для влажного насыщенного пара понятие степень сухости и обозначим степень сухости пара – 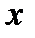. Степень сухости пара представляет собой отношение массы сухого насыщенного пара к массе влажного насыщенного пара :

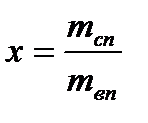
Тогда на пограничной кривой раздела жидкости и влажного насыщенного пара сухого насыщенного пара нет и 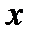= 0. На пограничной линии влажный насыщенный пар – перегретый пар – весь пар является сухим насыщенным, а влажного насыщенного пара уже нет, таким образом, = 1. Условимся все параметры на пограничной линии 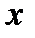= 0 обозначать с одним штрихом, а на линии = 1 – с двумя штрихами.

При проведении нашей серии опытов при понижении давления мы достигнем такого давления, когда влажный насыщенный пар начнет образовываться уже при температуре, когда возможно существование твердой фазы. Точка, в которой возможно существование в динамическом равновесии сразу трех фаз состояния вещества называют тройной точки и для воды параметры состояния в тройной точке принимают значение Т_F = 273,16 К и р_F =610,8 Па.

С другой стороны, при повышении давления, достигаем такой точки, где сходятся две пограничные линии = 0 и 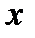= 1. Эта точка называется критической. Критическая точка характеризуется отсутствием границы раздела между жидкой и газообразной фазами, а удельные объемы жидкости и насыщенного пара в критической точке становятся одинаковыми. Параметры в точке называют критическими. Так для воды критическая температура Т_к = 647,3 К, а критическое давление р_к = 22,129 МПа.

То количество теплоты, которое нужно подвести к одному кг жидкости, находящейся при температуре кипения при постоянном давлении для превращения ее в сухой насыщенный пар называется удельной теплотой парообразования:

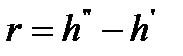
Исследуемый процесс можно отобразить в и диаграммах. Последняя удобна для определения функций состояния системы. Так, для определения функций состояния в 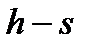диаграмме для влажного насыщенного пара достаточно знать давление или температуру и степень сухост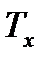и ( или ); для сухого насыщенного пара – степень сухости = 1, поэтому достаточно знать 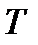или , или и, наконец, для перегретого пара нужно знать и и .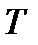

Также величины, характеризующие состояние влажного насыщенного пара определяются из выражений:

- для удельного объема:

-для удельной энтальпии: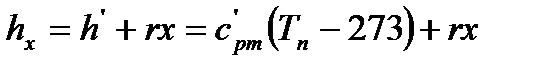

- для удельной энтропии:

где 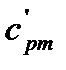– средняя в диапазоне температур (273 - ) удельная изобарная теплоемкость воды.

 

В большинстве тепловых двигателей в качестве рабочего тела выступает воздух. Рассмотрим основные понятия, связанные с воздухом.

Сухой воздух это характерная смесь газов без примесей молекул воды (водяного пара). Смесь сухого воздуха с водяным паром называется влажным воздухом. При малом парциальном давлении водяного пара смесь можно рассматривать как идеальный газ.

Если мы возьмем такой объем влажного воздуха, который бы содержал 1 кг сухого воздуха и 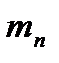грамм пара, то масса водяного пара, находящегося в таком объеме влажном воздуха, называется влагосодержанием, обозначается 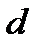и измеряется в граммах на кг. Значение влагосодержания можно определить следующим образом. Пусть в объеме влажного воздуха , находящегося под давлением и имеющего 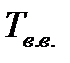содержится 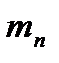грамм водяного пара и кг сухого воздуха. Запишем уравнение состояния для сухого воздуха и водяного пара.

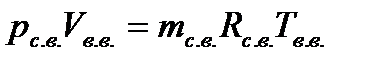
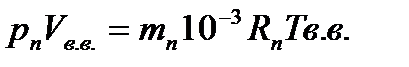
Разделив почленно записанные уравнения, получим выражение для определения влагосодержания:

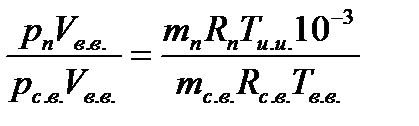
следовательно:

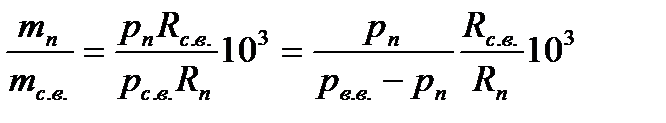
и тогда

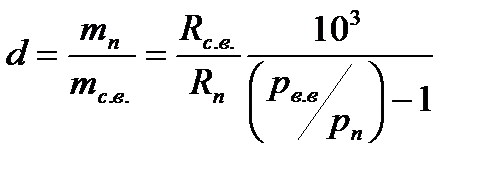
Максимальное влагосодержание воздуха при определенной температуре будет достигнуто тогда, когда пар во влажном воздухе станет насыщенным, т.е. парциальное давление пара в смеси станет равно парциальному давлению сухого насыщенного пара. Такой влажный воздух называется насыщенным влажным воздухом и влагосодержание его максимально. Очевидно, что повышение температуры влажного насыщенного воздуха будет сопровождаться повышением давления пара и, следовательно, пар перейдет в состояние перегретого, если влагосодержание его останется постоянным. Если с повышением температуры воздух останется влажным насыщенным, то влагосодержание его возрастет.

Масса водяного пара в граммах в одном м ³ влажного воздуха называется абсолютной влажностью воздуха, обозначается a и выражается в граммах на кубический метр. Ясно, что максимальную абсолютную влажность при конкретной температуре будет иметь влажный насыщенный воздух с сухим насыщенным паром. Тогда отношение абсолютной влажности влажного воздуха к абсолютной влажности насыщенного воздуха называется относительной влажностью воздуха , выражается в %. При понижении температуры влажного воздуха, который содержит перегретый пар, сначала он достигнет состояния влажного насыщенного воздуха с сухим насыщенным паром, а при дальнейшем понижении температура пар в воздухе станет влажным насыщенным, т е. воздух будет характеризоваться наличием капель влаги – тумана. Температура, при которой из воздуха начинает выделяться влага в виде тумана, называют температурой точки росы, и обычно выражается в ^оС.

Таблицы параметров и диаграммы состояния влажного воздуха доступны в справочниках. Наиболее удобными для расчетов и общепринятыми теплотехниками являются диаграммы , предложенные в 1918 г. проф. Л.К.Рамзиным, рис. 3.2. Диаграммы Рамзина требуют некоторых разъяснений.

 

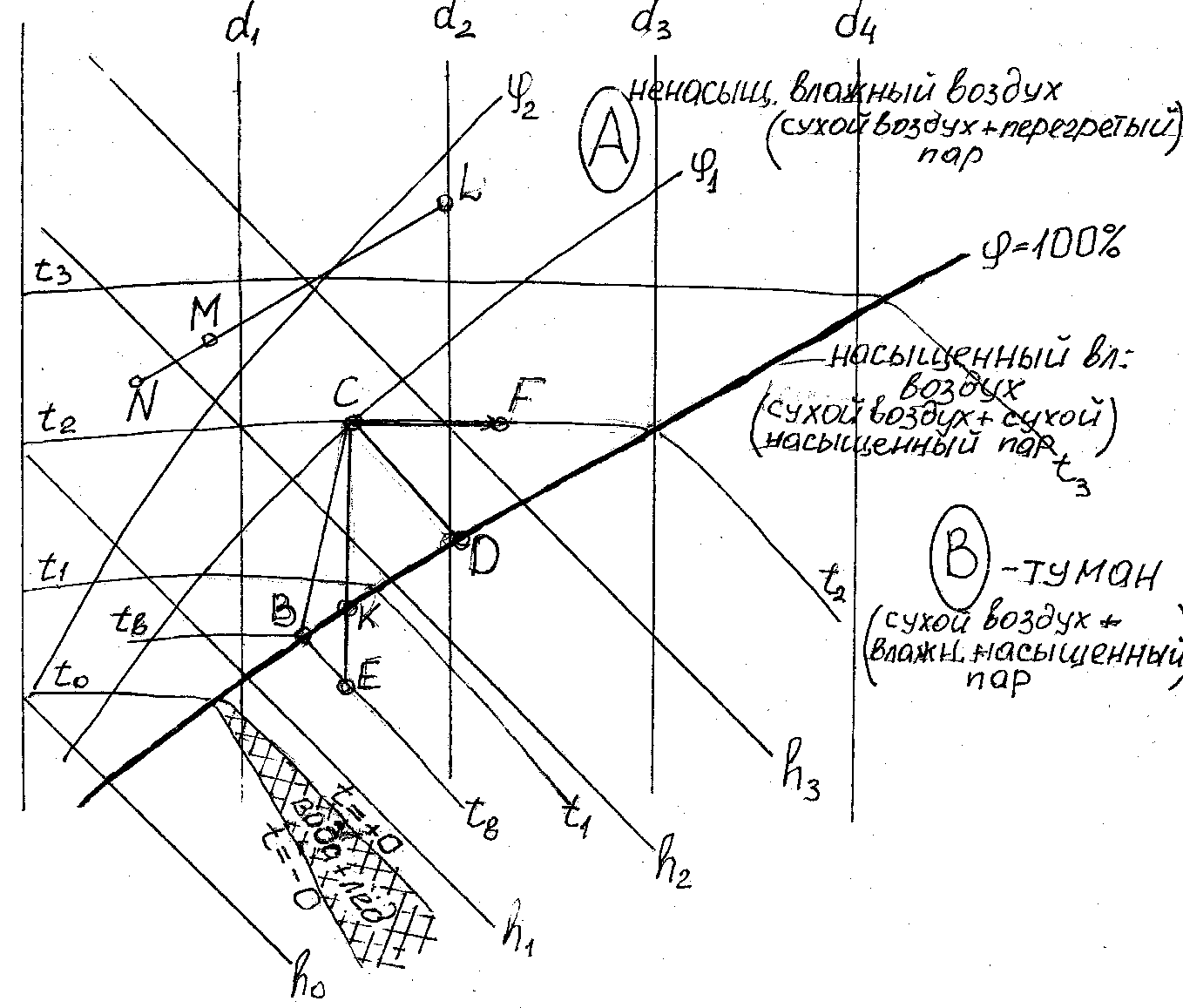
Рис.3.2. Диаграмма состояния влажного воздуха

 

По оси ординат на них откладывается удельная энтальпия, по оси абсцисс – влагосодержание. Для расширения поля диаграммы ось абсцисс повернута на 135^о относительно оси ординат, на диаграмме ее не проводят а заменяют горизонтальной линией, на которой отложен масштаб влагосодержания. Диаграммы построены для разных давлений (обычно, для 745 и 760 мм рт. ст., что соответствует 99,3 и 101,3 КПа). Линия = 100% делит поле диаграммы на область ненасыщенного влажного воздуха, содержащего перегретый пар (область А) и на область влажного воздуха с насыщенным влажным паром, т.е. область тумана (область В). Есть еще одна особая область, находящаяся между двумя изотермами и Т 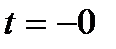, в которой присутствуют одновременно сухой воздух, влажный насыщенный пар и кристаллы льда.

Допустим, воздух имеет параметры, соответствующие точке С на диаграмме, то при охлаждении влажного воздуха, его влагосодержание остается постоянным, вплоть до точки К, пока относительная влажность не достигнет 100% (до температуры точки росы). Линия этого процесса на диаграмме вертикальна – С-К. Если продолжать охлаждение воздуха, например, до температуры t_в, то получится туман, а влажный насыщенный воздух при этом будет иметь параметры, соответствующие точке В. В этом случае количество выделившейся из влажного насыщенного воздуха влаги будет определяться разностью влагосодержания между точками Е и В. В случае отделения влаги, процесс охлаждения влажного воздуха между температурам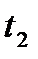и и 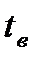этот процесс на диаграмме Рамзина отобразится условно отрезком С-В. Если во влажном воздухе произвести распыление воды, то вода начнет испаряться (если воздух не является влажным насыщенным), так как пар во влажном воздухе в состоянии перегретого пара. Учитывая, что можно принять удельную энтальпию воды ничтожной по сравнению с удельной энтальпией воздуха, а теплота воздуха, затраченная на испарение воды, возвращается к нему с испаренной влагой, то процесс можем рассматривать как изоэнтальпийный. И такой процесс отобразится на диаграмме в виде отрезка С-D. С другой стороны, если воздух в состоянии точки С увлажнять паром, то температура воздуха практически не изменится и на диаграмме изотермический процесс отображается С-F. И. наконец, рассмотрим смешивание двух потоков воздуха с параметрами, характеризуемыми точками N и L. То параметры потока определятся точкой М, лежащей на отрезке N-L, а соотношение длин отрезков NM и ML, равно соотношению массовых расходов потоков, причем точка М лежит ближе к параметрам потока, имеющего больший массовый расход.

 

Рассмотрим далее течение газов. А для этого представим канал произвольной формы, по которому протекает газ. Для вывода уравнений, описывающих течение газа, введем допущения о том, что трение в канале отсутствует, газ идеальный и наша термодинамическая система представляет собой открытую термодинамическую систему и процессы в ней обратимы. Выделим два произвольных сечения площадью 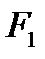и .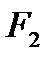

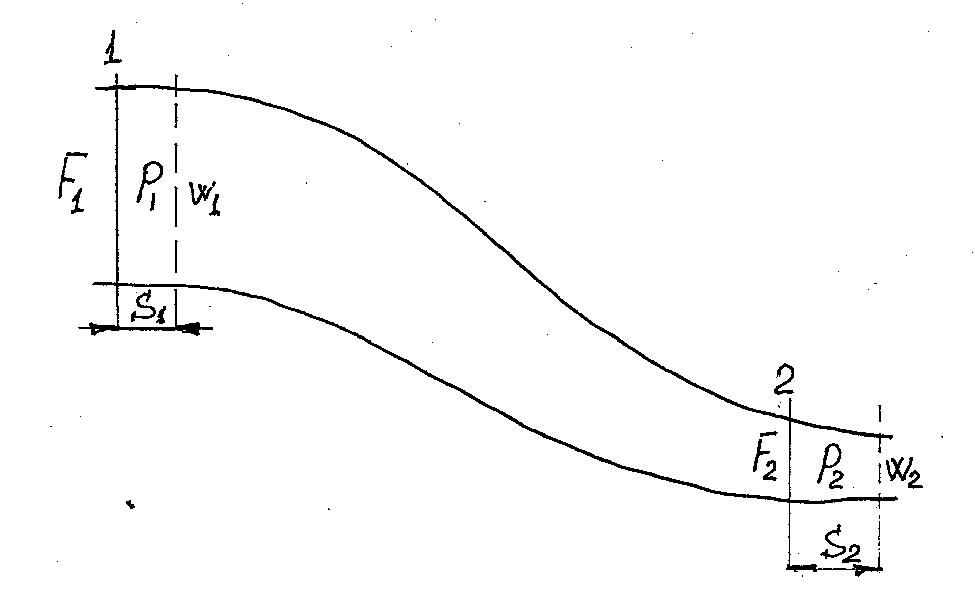
Рис. 3.3. Течение газа в канале

 

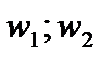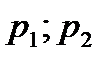При этом газ в сечениях 1 и 2, выделенных на рис. 3.3 имеет скорости и давления и соответственно и воспользуемся законом сохранения энергии или, иначе, первой основой термодинамики в виде:

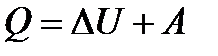
Детализируем работу 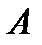, которая состоит собственно из работы по перемещению газа (иногда называют работой проталкивания) _, работы по изменению кинетической энергии газа и работы по преодолению перепада высот . Работа по перемещению газа в сечении на элементарное расстояние составит: , обратим внимание на то, что работа совершается из вне над системой, поэтому она отрицательна, работа на выходе из системы совершает система, следовательно, она положительна и составит соответственно: 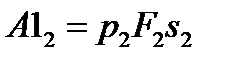. Работа 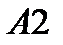по изменению кинетической энергии газа описывается уравнением:

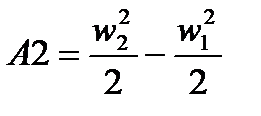
Работу по преодолению разности высот обозначим как:

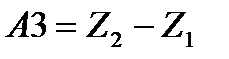
Тогда, подставив значение детализированных работ в уравнение сохранения энергии, и, принимая во внимание, что произведение на 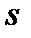есть не что иное, как объем, получаем:

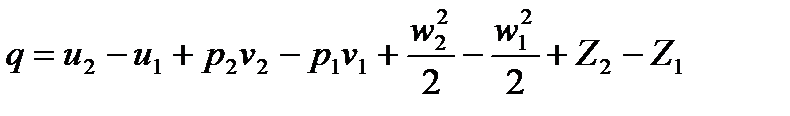
Рассмотрим адиабатное течение газа и, значит положим 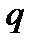= 0, тогда можно перегруппировать члены уравнения и вывести, что

Позволим себе продифференцировать это выражение, и получаем закон сохранения энергии в дифференциальной форме.

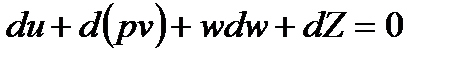
Нужно сказать, что в технике редко используют большие перепады высот, поэтому, пренебрегая соответствующим членом уравнения и, памятуя, что , запишем, что:

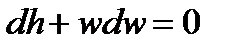
Далее вспомним, что в адиабатном процессе изменение внутренней энергии системы 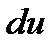идет только на совершение работы, а, следовательно,

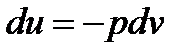
тогда подставим это выражение в дифференциальное уравнение сохранения энергии

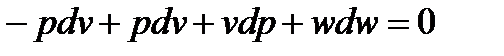
или

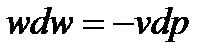
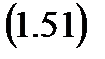
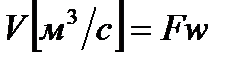Рассматривая нашу термодинамическую систему, мы полагали, что массовый расход газа через выбранные сечения постоянен , а объемный расход , тогда уместно будет, что

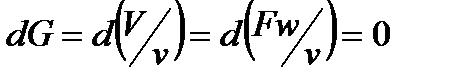
Продифференцируем и получим

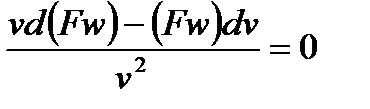
и далее:

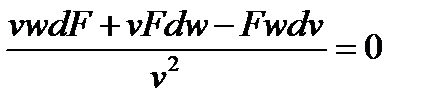
Выполнив математические преобразования, получим уравнение неразрывности:

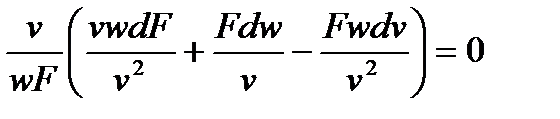
или

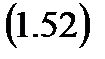
Теперь вернемся к уравнению первого закона термодинамики для адиабатного течения газа (1.51) и, для начала умножим его правую и левую части на 1/w², получим:

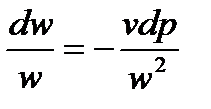
Далее умножим и разделим правую часть равенства на kp:

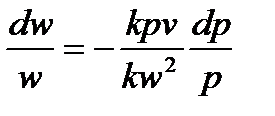
Но из физики известно, что местная скорость звука в газе 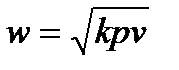. Введем отношение скорости течения газа к скорости звука, обозначим это отношение 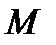и назовем его числом Маха, т.е.: и тогда:

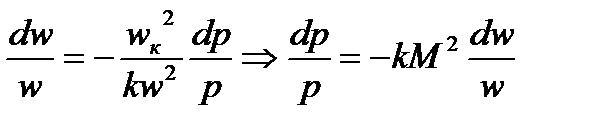
Теперь подставим это значение в уравнение неразрывности, а для этого вспомним, что 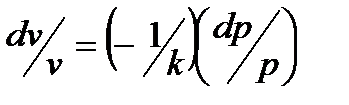, можем исключить :

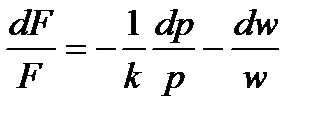
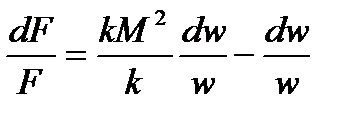
или:

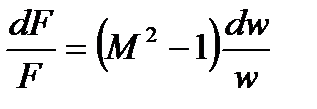
Аналогично можем исключить из рассмотрения .

Так как:

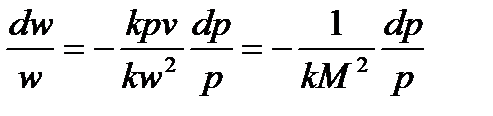
тогда:

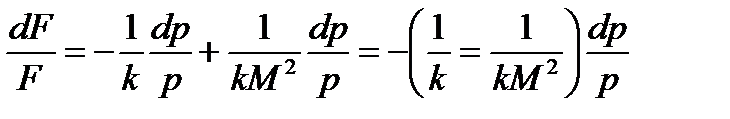
Следовательно:

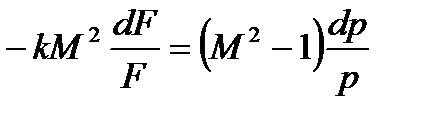
Рассмотрим более пристально полученные зависимости. Допустим , т.е. течение в нашем канале дозвуковое, тогда отрицательное. Следовательно, если 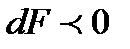, иными словами говоря, канал сужается, а такие каналы называют соплами, то скорость увеличивается и , при этом 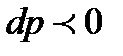т.е. давление падает. Таким образом, при адиабатном дозвуковом течении газа в сопле увеличивается скорость газа, а давление понижается, тогда в расширяющемся канале, а он в технике называется диффузор, происходит в строгом соответствии с полученными зависимостями снижение скорости течения газа при одновременном увеличении давления. Если скорость течения в сопле достигает при определенных условиях скорости звука, 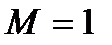, то выражение 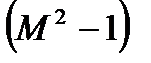становится равным нулю и тогда правая часть наших уравнений превращается в 0 и 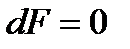. Такое течение называется критическим и все параметры, относящиеся к этому состоянию, называют критическими. Из этого следует важное заключение, что получить сверхзвуковую скорость в сужающемся канале невозможно, а можно только достичь скорости звука. Теперь рассмотрим сверхзвуковой поток с 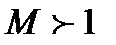. В этом случае выражение 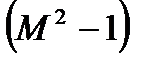становится положительным. Тогда, проводя аналогичные рассуждения, получаем, что при адиабатном сверхзвуковом течении газа для повышения скорости течения 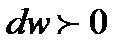, нужно иметь расширяющийся канал с 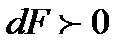(при этом давление в потоке будет уменьшаться ). Любопытно, что для того чтобы получить сверхзвуковую скорость в сопле, после достижения критического сечения, в котором скорость течения газа сравнивается с местной скоростью звука, требуется производить расширение канала. Такой канал называется соплом Лаваля.

В заключении к рассмотрению вопросов течения газов, воспроизведем без выводов некоторые полезные на практике зависимости. Итак, скорость газа в соплах можно определить из закона сохранения энергии с использованием энтальпии:

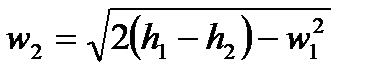
Как правило, скорость газа на входе в сопло мала настолько, что ею можно пренебречь и тогда:

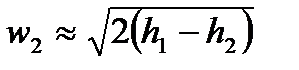
Вышеприведенное уравнение удобно для определения скорости газа в соплах при помощи h-s диаграмм. Из этого уравнения, используя ранее выведенные формулы для изменения энтальпии , уравнения адиабаты 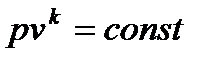и закона Клапейрона, можно получить:

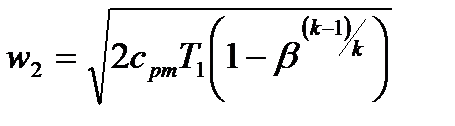
Здесь . Если положить , то:

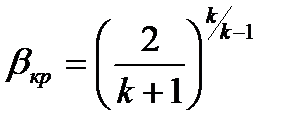
Как следует из рассуждений, если давление окружающей среды в которую истекает газ из сопла меньше или равно ,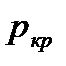

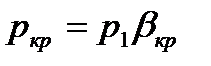
то скорость будет звуковой и определится, как 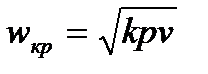. При этом скорость на выходе из сопла не зависит от давления окружающей среды, так как в устье сопла устанавливается давление , отличающееся от давления окружающей среды. Это явление объясняется тем, что волна давления, распространяющаяся со скоростью звука, будет сноситься потоком и не достигать устья сопла.

Массовый секундный расход газа определяется по уравнению для параметров в устье сопла:

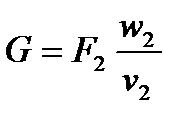
А так же

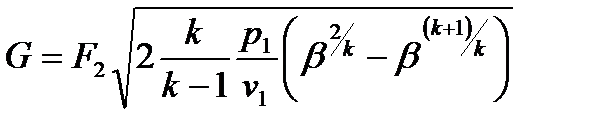
Расход газа в случае, если устанавливается критический режим течения газа с местной скоростью звука, при давлении окружающей среды менее 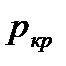, не зависит от давления окружающей среды, так как 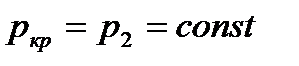. Когда давление окружающей среды превышает , то становится равным давлению окружающей среды, а расход – зависимым от давления окружающей среды.

Течение реального газа в сопле всегда связано с трением газа о стенки, и внутренним вязкостным трением – т.е. с некоторыми потерями. По этой причине процесс не является обратимым, а для учета этого обстоятельства вводятся поправочные коэффициенты:

коэффициент скорости сопла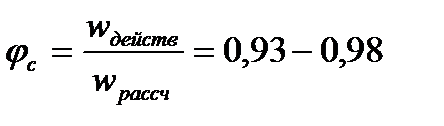

коэффициент расхода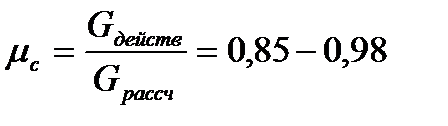

Приведенные коэффициенты зависят от качества обработки поверхности, размеров и пр.

Также в расчетах часто используются условные проходные сечения, 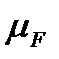, например, для расчетов истечения топлива из форсунок.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: