Лекция № 4. Законы передачи тепловой энергии. Теплообменные аппараты

В начале рассмотрения вопросов передачи тепловой энергии примем за аксиому тот факт, что тепло может передаваться только от более нагретого вещества менее нагретому.

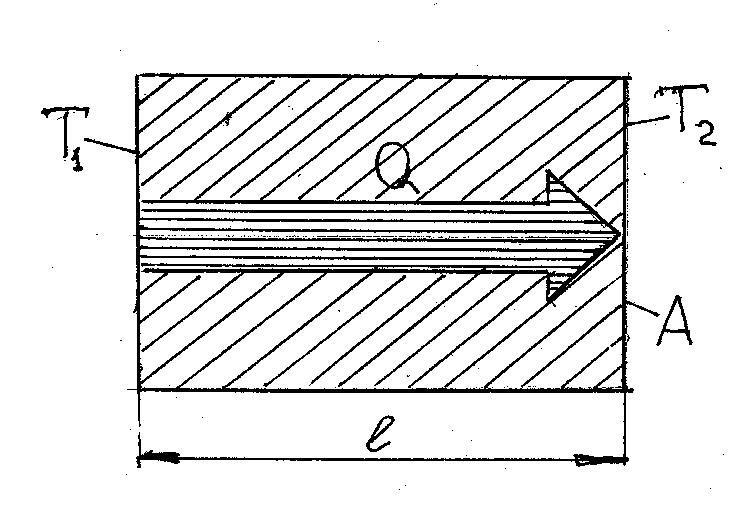
Рис. 4.1. Теплопроводность

 

Рассмотрим некоторый объем вещества, рис.4.1, через поверхность которого площадью , м² передается тепловая энергия , Дж в течение времени ,с, а поверхности имеют постоянные и одинаковые температуры и . Повышенная температура стенки связана с повышенной скоростью движения и повышенной энергией движения молекул, которые способны передавать часть своей энергии соседним молекулам, тем самым увеличивая их скорость движения и, соответственно, энергию. Длину проводника тепла, в направлении по которому идет тепловая энергия, обозначим . Пусть этот процесс идет бесконечно долго и тогда его можно рассматривать как установившийся и стационарный. Тогда можно сказать, что количество тепловой энергии, проходящей через выделенный объем вещества, пропорционален разности температур, площади поверхности и времени и обратно пропорционален длине проводника.

Коэффициент пропорциональности называется коэффициентом теплопроводности материала проводника и измеряется в Вт/мК.

Введем дополнительные определения. Количество теплоты, проходящее через выбранную площадь поверхности проводника в единицу времени называется тепловым потоком , Вт, а отношение теплового потока к единице площади поверхности назовем поверхностной плотностью теплового потока, Вт/м².

Поверхностная плотность теплового потока является вектором, направление которого совпадает с направлением распространения (передачи) теплоты. Вектор, направленный к нормали изотермической поверхности в сторону увеличения температуры и численно равный частной производной от температуры по этому направлению, называется градиентом температуры

Тогда из наших размышлений вытекает, что:

Это выражение называется законом Фурье, который описывает механизм теплопроводности и гласит о том, что вектор поверхностной плотности теплового потока пропорционален температурному градиенту и имеет противоположное направление. Коэффициент теплопроводности или просто теплопроводность материала, представляющая собой поверхностную плотность теплового потока при градиенте температуры, равном единице, – величина справочная, получаемая экспериментальным путем. Теплопроводность является физическим свойством вещества и характеризует способность вещества проводить теплоту. В расчетах учитывают, что она, теплопроводность, зависит от температуры.

Минимальную теплопроводность имеют газы (от 0,005 до 0,5 Вт/мК), максимальную – металлы (от 2,5 до 420 Вт/мК). Материалы с малой теплопроводностью, обычно менее 0,25 Вт/мК используют для теплоизоляции и называют теплоизоляционными.

Для технических расчетов, в частности, возникающих в деталях тепловых напряжений, требуется знать распределение температур в объеме деталей. Совокупность значений температур для всех точек пространства в исследуемом объеме в определенный момент времени называется температурным полем.

В самом общем случае, температурное поле тела описывается уравнением

Если температура не зависит от времени, то такое температурное поле называют стационарным. Ввиду того, что в циклически работающих машинах, такое редко достижимо, то, зачастую, для упрощения расчетов поле рассматривается как квазистационарное (т.е. как стационарное для определенного промежутка времени).

Для решения задач, связанных с построением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности. Такое уравнение выводится из первого закона термодинамики для тел, процесс взаимодействия которых с окружающей средой, происходит без совершения какой либо внешней работы. Если рассмотреть процесс распространения теплоты теплопроводностью для выделенного элемента тела (например, кубика с гранями ), то уравнение первого закона термодинамики примет вид:

где – теплота, выделившаяся внутри элемента, Дж.

Допустим, что процесс происходит без выделения энергии внутри рассматриваемого элемента, а физические параметры тела (теплопроводность , теплоемкость и плотность ), тогда, используя закон Фурье, можно вывести дифференциальное уравнение теплопроводности для твердого тела и, в конечном виде, оно принимает вид:

Обычно, коэффициент пропорциональности обозначают и называют температуропроводностью, м²/с, которая тоже является физическим параметром вещества. Из уравнения видно, что изменение температуры во времени для любой точки пространства пропорционально температуропроводности материала.

Если рассмотреть частный случай, когда процесс стационарен и тепло распространяется только в одну сторону, например, по оси , то, говорят, что температурное поле является стационарным и одномерным и уравнение теплопроводности принимает вид:

А если материал однороден, т.е. имеет неизменные значения , то уравнение упрощается до:

При решении дифференциального уравнения теплопроводности для конкретного случая нужно иметь дополнительные данные, а именно, формы и размеры тела, его теплофизические свойства, исходное состояние температурного поля и закономерности теплообмена на границе тела или детали с окружающей средой (граничные условия). Граничные условия могут быть заданы тремя способами. Граничные условия первого рода – задается распределение температуры на поверхности тела (для каждого момента времени, если не рассматривается стационарный режим теплопроводности). Граничные условия второго рода – задаются значениями теплового потока для каждой точки поверхности тела (и момента времени). И, наконец, граничные условия третьего рода – задаются температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой.

В самом простом случае, при рассмотрении стационарного режима теплопроводности для плоской стенки толщиной , граничные условия первого рода выглядят как: при и при 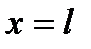. Тогда, решая уравнение теплопроводности, получаем, что:

а, для поверхностной плотности теплового потока:

Из уравнений видно, что для плоской стенки, распределение температуры по ее глубине носит линейный характер.

Для аналогичного рассмотрения теплопроводности через бесконечную цилиндрическую стенку потребуется ввести цилиндрическую систему координат и в ней уравнение запишется как:

Или

После решения получим

где и – постоянные интегрирования, определяемые из граничных условий. Из последнего уравнения видно, что по толщине цилиндрической стенки температура распределяется по логарифмическому закону. Граничные условия первого рода для цилиндрической стенки имеют вид:

при , , а при , ,

где и внутренний и наружный радиусы стенки.

В общем случае дифференциальное уравнение теплопроводности решается приближенными численными методами (конечных разностей, конечных элементов и др.).

 

Жидкие или газообразные тела, вступающие в контакт с твердым телом, находящимся при другой температуре, либо отдают ему тепло, либо получают тепло от него. Такое явление называют теплоотдачей.

 

 

Рис. 4.2. Теплоотдача

 

Рассмотрим плоскую стенку площадью , которая омывается жидкостью или газом, при этом разность температур между средами обозначим, как , рис.4.2. Пусть процесс теплоотдачи происходит определенное время , а количество тепла, передаваемого в процессе - . Тогда можно записать:

То есть, количество передаваемой энергии при теплоотдаче пропорционально площади поверхности теплоотдачи, времени и разности температур. Коэффициент пропорциональности называют коэффициентом теплоотдачи, Вт/м²К, который зависит от состава жидкости или газа и скорости его движения, а так же от обработки поверхности твердого тела, но не от его состава и теплофизических свойств.

Если воспользоваться поверхностной плотность теплового потока , то получим.

Это полученное выражение называется законом Ньютона-Рихмана. График изменения температуры при теплоотдаче представлен на рис. 4.3.

 

 

Рис. 4.3. Температурная диаграмма теплоотдачи

 

Рассматривая вопросы теплоотдачи нельзя забывать о том, что жидкость или газ, рассматриваемые в процессе, являются подвижными, а это значит, что перенос тепла будет обусловлен перемещением некоторых макро объемов жидкости или газа даже в том случае, если газ или жидкость, омывающие стенку, в целом, неподвижен. При нагреве газ или жидкость изменяет свою плотность и, следовательно, нагретые объемы будут подниматься вверх, а их места будут заняты более холодным веществом из объема. Такое явление называется конвекцией, а теплообмен конвективным.

Принимая во внимание вышесказанное, становится очевидным, что аналитический расчет коэффициента теплоотдачи является весьма затруднительным. Тем не менее, для простых случаев (например, для течения в гладкой трубе) с определенными допущениями, аналитические формулы имеются. В основном же, формулы для определения коэффициентов теплоотдачи получены на основе теория подобия и использования критериальных зависимостей.

 

Рассмотрим случай, когда два объема жидких или газообразных тел (или комбинации их), имеющие различную температуру разделены твердым телом (плоской перегородкой, для начала). Тогда процесс передачи теплоты происходит в три стадии. Сначала, теплоотдача из первой среды, имеющей высокую температуру, к поверхности перегородки – теплоотдача. Затем передача энергии за счет теплопроводности через стенку-перегородку. И, наконец, теплоотдача от стенки к среде с более низкой температурой. Совокупность этих трех процессов называется теплопередачей.

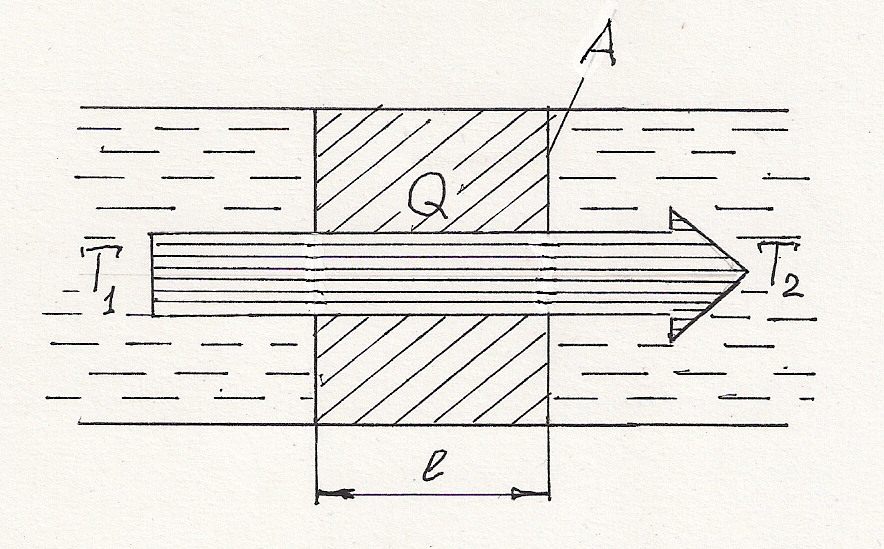
Рис.4.4. Теплопередача

 

Если через поверхность перегородки (см. рис. 4.4.), имеющей толщину , передается количество теплоты 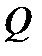, в течение продолжительности процесса 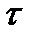, то, с учетом того, что тепловой поток на всех стадиях теплообмена должен оставаться постоянным, можно записать:

 

 

Рис. 4.5. График изменения температур при теплопередаче

 

При этом сумма всех разностей температур на рис. 4.5 равна разности между температурами двух сред. А из этого следует, что

 

Если из этого выражения вынести за скобки , то

Величина, обратная выражению в скобках называется коэффициентом теплопередачи . Таким образом, процесс теплопередачи описывается формулой:

Тогда поверхностная плотность потока для плоской стенки имеет вид

Где для плоской стенки:

А для цилиндрической:

 

 

Все законы передачи тепловой энергии, рассмотренные выше, относятся к процессам передачи тепла в той или иной мере, связанной с передачей энергии молекулами вещества. Но тепловая энергия еще может переноситься от одного тела к другому благодаря испусканию и поглощению электромагнитных волн.

Пусть:

- поток (мощность) падающего излучения,

- поток отраженного излучения,

- поток поглощенного излучения,

- поток прошедшего излучения, (см. рис. 4.6.).

 

 

Рис. 4.6. Излучение

 

Тогда коэффициент отражения тела

Коэффициент поглощения

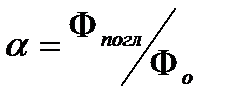
Коэффициент пропускания

Следует обратить внимание на то, что эти коэффициенты зависят от свойств самого тела и длинны волны падающего излучения. Согласно закону сохранения энергии,

Если в этом выражении левую и правую части разделить на , получим

Тело, для которого коэффициент отражения и коэффициент пропускания равны нулю, а коэффициент поглощения равен единице, что не реализуется на практике, называется абсолютно черным телом.

Любое тело с температурой больше 0 К, испускает излучение. Такое излучение называется температурным или тепловым излучением.

Излучение абсолютно черного тела превышает излучение любых других тел при данной длине волны. Его излучательная способность, подобно коэффициенту поглощения равна единице.

Излучательная способность любого тела равна его коэффициенту поглощения при заданной температуре и длине волны 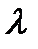. Это закон – закон излучения Киргофа:

Если – поток излучения, испускаемый реальным (серым) телом с определенной температурой, а – поток излучения черного тела с той же температурой, то из закона Киргофа следует

Таким образом, мощность (поток) излучения любого серого тела равна мощности излучения черного тела с той же температурой, умноженной на излучательную способность данного тела.

Пусть – мощность излучения, испускаемая нагретым телом, 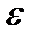- излучательная способность тела, – площадь поверхности излучения, – температура излучающего тела, - температура окружающей среды, то можно сказать, что мощность излучения, испускаемая нагретым телом, пропорциональна площади и четвертой степени температуры тела. Коэффициент пропорциональности называется постоянной Стефана-Больцмана и численно равен Вт/м²К⁴. Тогда мощность излучения нагретого тела:

Это выражение называется законом Стефана-Больцмана. Но излучающее тело одновременно с излучением поглощает излучение, испускаемое окружающей средой и имеющее мощность

и, если площадь излучающей и поглощающей поверхности равны (что бывает не всегда!), то закон Стефана-Больцмана запишется в виде:

Произведение постоянной Стефана-Больцмана на излучательную способность тела называют коэффициентом излучения, который зависит от свойств вещества. Следует особо обратить внимание на то, что мощность излучения, вычисленная по закону Стефана-Больцмана, приходится на весь спектр излучения, т.е. на все длины волн. Распределение же мощности по длинам волн неравномерно. Это распределение мощности излучения, приходящееся на отдельные интервалы длин волн в зависимости от температуры тела определяется законом Планка. Причем с изменением температуры тела, максимум распределения мощности излучения приходится на разные значения длин волн – это закон, который носит название: закон смещения Вина. Закон устанавливает, что с повышением температуры доля коротковолнового излучения в спектре увеличивается. Поэтому цвет излучения может служить характеристикой температуры излучения (цветовая температура).

В тепловых машинах условия, когда процесс передачи тепла излучением является превалирующим над процессами теплопередачи, встречается не очень часто (за исключением случаев рассмотрения процессов горения, когда доля лучистой энергии в составляющих тепловых потоков от рабочего тела может составлять до 30%). Поэтому на практике при расчете процессов передачи тепловой энергии долю излучения учитывают за счет некоторого увеличения коэффициентов теплопередачи или теплоотдачи.

Технические устройства, в которых происходит процесс теплопередачи между двумя или несколькими теплоносителями называются теплообменными аппаратами или теплообменниками. Самым простым устройством по принципу действия является аппарат, в котором теплообмен между теплоносителями осуществляется за счет их смешения. Такие теплообменники, в которых происходит непосредственный контакт и смешение теплоносителей называются теплообменникамисмесительного типа. Те аппараты, в которых нет непосредственного контакта теплоносителей между собой, а процесс теплообмена происходит через твердую поверхность, называются теплообменниками поверхностного типа.

Теплота через твердую стенку от горячего теплоносителя к холодному может передаваться двумя способами. Если одна и та же твердая поверхность теплообменника попеременно омывается, то горячим, то холодным теплоносителем, при этом имеет место механизм теплоотдачи, то такие теплообменники называются регенеративными.

Наибольшее распространение в СЭУ имеют рекуперативные теплообменники, в которых теплоносители протекают одновременно, но разделены твердой поверхностью (стенкой), через которую происходит классическая теплопередача. Преимущественно применяются трубчатые теплообменники, в которых один теплоноситель проходит по трубкам, а другой – в корпусе, снаружи трубок. По взаимному движению теплоносителей, теплообменники бывают:

- прямоточные, в которых горячий и холодный теплоносители движутся в одном направлении;

- противоточные, когда теплоносители движутся в противоположных направлениях;

- с перекрестным током:

- комбинированные.

В качестве горячего теплоносителя в теплообменниках выступают вода, масло, воздух отработавшие газы и др. среды, а в качестве холодного – как правило, забортная вода. Часто, когда теплообменник выполняет одну функцию – охлаждение теплоносителя, аппарат называют холодильником или охладителем.

Анализ и выбор схем движения теплоносителей в теплообменных аппаратах производится путем теплового, гидродинамического и прочностного расчетов по специальным программам с использованием методов моделирования. Как показывают расчеты и практика конструирования и эксплуатации, наиболее предпочтительной схемой, например, для охладителей надувочного воздуха является перекрестный ток воздуха и воды с двумя или более ходами. Для теплообменников, водо-водяных и водомасляных, в основном, используется схема с большим количеством перегородок в межтрубном пространстве и одним трубным ходом (правда, не всегда) и схемы противотока.

Для проведения анализа эффективности работы рекуперативных теплообменных аппаратов рассмотрим каждый из теплоносителей как открытую термодинамическую систему. Обозначим параметры, относящиеся к горячему теплоносителю, индексом 1, а индексом 2 – к холодному. Параметры с одним штрихом пусть относятся к входу в теплообменник, с двумя – к выходу.

Для анализа запишем уравнение первого закона термодинамики в виде:

Поскольку в теплообменнике не совершается работы, то

Следовательно, уменьшение удельной энтальпии горячего теплоносителя связано с адекватным увеличением удельной энтальпии холодного теплоносителя. Тогда справедливо уравнение теплового баланса теплообменника

Здесь - расход теплоносителя; - изобарная теплоемкость теплоносителя, а - коэффициент, учитывающий диссипацию (рассеивание) тепловой энергии – коэффициент диссипации.

Если взять средние изобарные теплоемкости масс теплоносителей, равных их массовым расходам, то

Рассмотрим изменение температур теплоносителей в теплообменнике, по мере их продвижения по устройству, показанное на рис.4.7. Если теплообменный аппарат прямоточный, то при равенстве теплоемкостей теплоносителей, они равноускоренно стремятся к средней температуре, приблизительно равной среднему арифметическому температур теплоносителей. Если при аналогичных условиях рассмотреть противоточный теплообменник, то, очевидно, что у него разность температур между горячим и холодным теплоносителем практически не изменяется от входа до выхода из аппарата.

В случае, если теплоемкость горячего теплоносителя 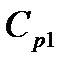больше теплоемкости холодного , то в прямоточном теплообменнике уменьшение температуры горячего теплоносителя будет происходить медленнее, чем увеличение температуры холодного. В противоточном теплообменнике разница между температурами теплоносителей по мере увеличения площади поверхности теплообмена будет увеличиваться.

Рис 4.7.Изменение температур теплоносителей в

теплообменных аппаратах рекуперативного типа

 

Если рассмотреть случай, когда меньше , то все будет с точностью до наоборот.

Необходимо отметить, что в противоточных теплообменниках может сложиться такая ситуация, когда температура холодного теплоносителя может превысить температуру горячего теплоносителя на выходе, чего в прямоточном теплообменнике не может произойти никогда.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: