Парная регрессия и метод наименьших квадратов

Будем предполагать в рамках модели (2.2) линейную зависимость между двумя переменными Y и X. Т.е. имеем модель парной регрессии в виде:

Y_i = a + bX_i + u_i, i =1,…, n.

а. E u_i =0, i =1,…, n.

б.

в. X ₁, …, X _n – неслучайные величины.

Предположим, что имеется выборка значений Y и X.

Обозначим арифметические средние (выборочные математические ожидания) для переменных X и Y:

.

Запишем уравнение оцениваемой линии в виде:

, (2.6)

где и - оценки неизвестных параметров a и b, а - ордината этой линии.

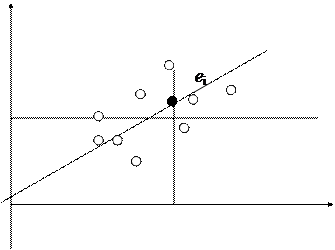
Пусть (X_i, Y_i) одна из пар наблюдений. Тогда отклонение этой точки (см. рис. 2.1) от оцениваемой линии будет равно e _i= Y _i - .

Принцип метода наименьших квадратов (МНК) заключается в выборе таких оценок и , для которых сумма квадратов отклонений для всех точек становится минимальной.

Y

 

 

X

 

Рис. 2.1. Иллюстрация принципа МНК

 

Необходимым условием для этого служит обращение в нуль частных производных функционала:

по каждому из параметров. Имеем:

Упростив последние равенства, получим стандартную форму нормальных уравнений, решение которых дает искомые оценки параметров:

(2.7)

Из (2.7) получаем:

(2.8)

Пример. Для иллюстрации вычислений при отыскании зависимости с помощью метода наименьших квадратов рассмотрим пример (табл. 2.1).

Таблица 2.1

Индивидуальное потребление и личные доходы (США, 1954-1965 гг.)

Год	Индивидуальное потребление, млрд. долл.	Личные доходы, млрд. долл.

 

Заметим, что исходные данные должны быть выражены величинами примерно одного порядка. Вычисления удобно организовать, как показано в таблице 2.2. Сначала рассчитываются , затем x _i, y _i. Результаты заносятся в столбцы 3 и 4. Далее определяются x _i², x _i y _i и заносятся в 5 и 6 столбцы таблицы 2.2. По формулам (2.8) получим искомые значения параметров =43145/46510=0,9276; =321,75-0,9276^.350=-2,91.

Оцененное уравнение регрессии запишется в виде =-2,91+0,9276 X.

Следующая важная проблема состоит в том, чтобы определить, насколько "хороши" полученные оценки и уравнение регрессии. Этот вопрос рассматривается по следующим стадиям исследования: квалифицирование (выяснение условий применимости результатов), определение качества оценок, проверка выполнения допущений метода наименьших квадратов.

Относительно квалифицирования уравнения =-2,91+0,9276 X. Оно выражает, конечно, достаточно сильное утверждение. Применять это уравнение для прогнозирования следует очень осторожно. Дело в том, что, даже отвлекаясь от многих факторов, влияющих на потребление, и от систематического изменения дохода по мере варьирования потребления, мы не располагаем достаточно представительной выборкой.

Таблица 2.2

Рабочая таблица расчетов (по данным табл. 2.1)

 

Год	X	Y	x	y	x 2	xy		ei
			-93	-85,75		7974,75	235,48	0,52
			-75	-67,75		5081,25	252,18	1,82
			-57	-54,75		3120,75	268,88	-1,88
			-41	-40,75		1670,75	283,72	-2,72
			-31	-31,75		984,25	292,99	-2,99
			-13	-10,75		139,75	309,69	1,31
				3,25			321,75	3,25
				13,25		185,5	334,74	0,26
				33,25		1163,75	354,22	0,78
				53,25		2928,75	372,77	2,23
				79,25		6894,75	402,45	-1,45
				109,25		13000,75	432,13	-1,13
å	=350,00	=321,75		0,00			=321,75	0,00

 

Полученное уравнение =-2,91+0,9276 X можно использовать для расчета точечного прогноза, в том числе и на ретроспективу. Подставляя последовательно значения X из второго столбца табл. 2.2 в уравнение =-2,91+0,9276 X, получим предпоследний столбец табл. 2.2 для прогнозных значений . Ошибка прогноза вычисляется по формуле e _i= Y _i - и дана в последнем столбце рабочей таблицы.

Заметим, что ошибка прогноза e _i фактически является оценкой значений u _i. График ошибки e _i представлен на рис. 2.2. Следует отметить факт равенства нулю суммы S e _i=0, что согласуется с первым ограничением модели парной регрессии - E u_i =0, i =1,…, n. Ñ

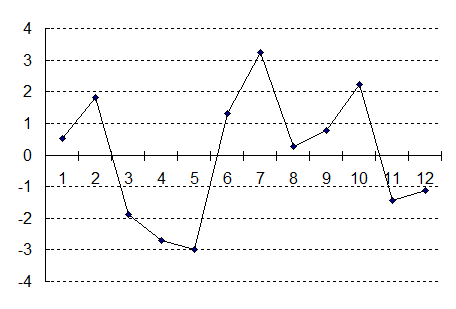
Рис. 2.2. График ошибки прогноза

 

В модели (2.2) функция f может быть и нелинейной. Причем выделяют два класса нелинейных регрессий:

q регрессии, нелинейные относительно включенной объясняющей переменной, но линейные по параметрам, например полиномы разных степеней - Y_i = a ₀ + a ₁ X_i + a ₂ X_i ²+ u_i, i =1,…, n или гипербола - Y_i = a ₀ + a ₁/ X_i + u _i, i =1,…, n;

q регрессии нелинейные по оцениваемым параметрам, например степенная функция - Y_i = a ₀ u_i, i =1,…, n, или показательная функция - Y_i = , i =1,…, n.

В первом случае МНК применяется так же, как и в линейной регрессии, поскольку после замены, например, в квадратичной параболе Y_i = a ₀ + a ₁ X_i + a ₂ X_i ²+ u_i переменной X_i ² на X _1i: X_i ²= X _1i, получаем линейное уравнение регрессии Y_i = a ₀ + a ₁ X_i + a ₂ X _1i+ u_i, i =1,…, n.

Во втором случае в зависимости от вида функции возможно применение линеаризующих преобразований, приводящих функцию к виду линейной. Например, для степенной функции Y_i = a ₀ u_i после логарифмирования получаем линейную функцию в логарифмах и применяем МНК.

Однако для, например, модели Y_i = a ₀+ a ₂ + u_i линеаризующее преобразование отсутствует, и приходится применять другие способы оценивания (например, нелинейный МНК).

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: