 |
4.1. Построение матрицы переноса
|
|
|
|
4. 1. Построение матрицы переноса
1. Формулировка общей задачи при произвольных начальных условиях:
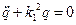 - дифференциальное уравнение движения;
- дифференциальное уравнение движения;
 :
: 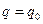 ,
, 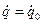 - начальные условия.
- начальные условия.
Решение для момента времени 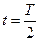 :
:
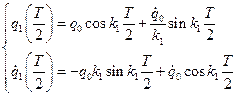
Решение в матричной форме:
 .
.
Или в компактной форме
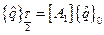 .
.
Здесь  - матрица переноса,
- матрица переноса,  - вектор состояния в конце полупериода;
- вектор состояния в конце полупериода;  - вектор состояния в начальный момент.
- вектор состояния в начальный момент.
2. Формализованная процедура построения матрицы переноса, основанная на рассмотрения двух частных задач при единичных начальных условиях:
Задача 1. Формулировка задачи: 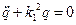 ;
;  :
:  ,
,  .
.
Решение:
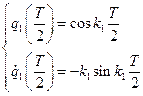 - элементы первого столбца матрицы переноса.
- элементы первого столбца матрицы переноса.
Задача 2. Формулировка задачи: 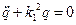 ;
;  :
: 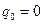 ,
, 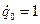 .
.
Решение:
 - элементы второго столбца матрицы переноса.
- элементы второго столбца матрицы переноса.
Общая задача. Формулировка общей задачи: 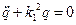 ;
;  :
:  ,
, 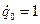 .
.
Решение общей задачи при единичных начальных условиях:
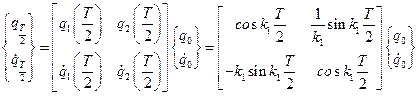 .
.
Здесь  - матрица переноса.
- матрица переноса.
4. 2. Уравнение Мейснера.
Рассмотрим возможный путь решения уравнения Мейснера для малого значения параметра 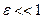
 .
.
Кроме тривиального решения 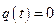 существует и другое решение, которое разыскивается в виде двухкомпонентного вектора
существует и другое решение, которое разыскивается в виде двухкомпонентного вектора  . Начальные условия задаются в виде:
. Начальные условия задаются в виде:  :
: 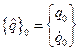 ; в конце периода, то есть при
; в конце периода, то есть при  :
: 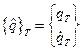 . Связь между векторами
. Связь между векторами 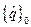 и
и  представим в виде линейного дифференциального уравнения
представим в виде линейного дифференциального уравнения
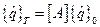 (4. 2)
(4. 2)
где 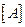 - матрица переноса.
- матрица переноса.
1. Уравнение (4. 2) на интервале  можно представить в виде
можно представить в виде
 (4. 3)
(4. 3)
Введем новую константу 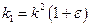 , тогда уравнение (4. 3) приобретает вид
, тогда уравнение (4. 3) приобретает вид
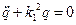 . (4. 4)
. (4. 4)
|
|
|
Построим матрицу переноса  исходя из уравнения
исходя из уравнения
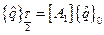 .
.
Первый столбец матрицы  строится путем интегрирования дифференциального уравнения (4. 4). Запишем начальные условия так: при
строится путем интегрирования дифференциального уравнения (4. 4). Запишем начальные условия так: при  :
:  ,
,  , поэтому
, поэтому  и
и 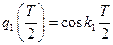 - это первый элемент первого столбца матрицы
- это первый элемент первого столбца матрицы  .
.
Второй элемент первого столбца матрицы  - это обобщенная скорость, поэтому при
- это обобщенная скорость, поэтому при 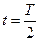 :
:  ; значит
; значит 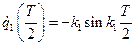 - второй элемент первого столбца матрицы
- второй элемент первого столбца матрицы  .
.
Для нахождения второго столбца матрицы  интегрируется уравнение (4. 4) при других начальных условиях:
интегрируется уравнение (4. 4) при других начальных условиях:  :
: 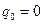 ,
, 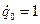 . Интеграл запишется в виде
. Интеграл запишется в виде  , поэтому первый элемент второго столбца матрицы
, поэтому первый элемент второго столбца матрицы  запишется в виде
запишется в виде 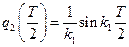 . Второй элемент второго столбца матрицы переноса определяется из условия
. Второй элемент второго столбца матрицы переноса определяется из условия  ; его значение будет равно:
; его значение будет равно:  .
.
Таким образом, найдена структура матрицы переноса
 ,
,
Следовательно, установлена взаимосвязь
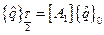 .
.
2. Уравнение (4. 2) на интервале  имеет вид
имеет вид
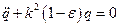 .
.
Вводя новую постоянную 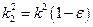 , преобразуем его к виду
, преобразуем его к виду
 . (4. 5)
. (4. 5)
Повторим процедуру построения матрицы переноса 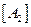 , определяющую вектор
, определяющую вектор  согласно уравнению
согласно уравнению
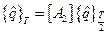 .
.
За начальную точку отсчета времени принимаем  , тогда начальные условия запишутся в виде:
, тогда начальные условия запишутся в виде:  :
:  ,
,  . Решая уравнение (4. 5), находим
. Решая уравнение (4. 5), находим
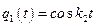 и
и  . Поэтому первый и второй элементы первого столбца матрицы переноса
. Поэтому первый и второй элементы первого столбца матрицы переноса 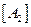 будут равны
будут равны 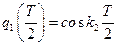 и
и  соответственно. Аналогично находим элементы второго столбца этой матрицы:
соответственно. Аналогично находим элементы второго столбца этой матрицы: 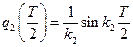 и
и  . Таким образом матрица
. Таким образом матрица 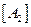 построена
построена

Можно показать, что матрица переноса 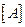 на интервале
на интервале  определяется согласно формуле
определяется согласно формуле
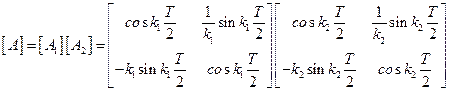 .
.
Повторяя описанную выше процедуру определенное число раз, можно построить матрицу переноса для соответствующего момента времени, кратного любому числу периодов
|
|
|
 ,
, 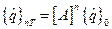 .
.
Иными словами по заданным начальным условиям можно получить решение через любое число периодов.
Изложенный подход часто используется для определения устойчивости колебательного движения:
1. Если решение  возрастает с течением времени, то движение неустойчивое;
возрастает с течением времени, то движение неустойчивое;
2. Если решение  убывает с течением времени, то движение устойчивое;
убывает с течением времени, то движение устойчивое;
3. Если амплитуда обобщенных координат не меняется с течением времени, то такие решения соответствуют границе раздела устойчивой области и неустойчивой.
Судить об устойчивости движения можно по норме матрицы  , величина которой определяется выражением
, величина которой определяется выражением
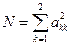 .
.
Если для оценки устойчивости используется матрица 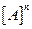 , то возможны следующие случаи движения:
, то возможны следующие случаи движения:
1.  - неустойчивое движение;
- неустойчивое движение;
2. 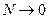 - устойчивое движение;
- устойчивое движение;
3.  - граница раздела между областями устойчивого и неустойчивого движения.
- граница раздела между областями устойчивого и неустойчивого движения.
Последний случай соответствует установившемуся периодическому движению, которое описывается уравнением:
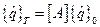 или
или 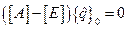 , где
, где  - единичная матрица. Это уравнение имеет нетривиальное решение если
- единичная матрица. Это уравнение имеет нетривиальное решение если  , то есть для определения границы между устойчивым и неустойчивым движениями можно использовать указанное условие.
, то есть для определения границы между устойчивым и неустойчивым движениями можно использовать указанное условие.
|
|
|


