 |
4.7. Параметрическое возбуждение колебаний по закону прямоугольного синуса.
|
|
|
|
В заключении этого раздела рассмотрим случай, когда закон изменения параметров системы соответствует функции 
. При решении этой задачи удается определить области неустойчивости (области параметрического резонанса) в замкнутой форме. Пример такой задачи – раскачивание математического маятника, изображенного на рис. 4. 2.
Уравнения движения маятника при скачкообразном изменении длины нити имеют вид
при 
;
при 
. (4. 14)
Обозначив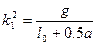 
; 
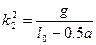, (4. 15)
запишем решение на каждом интервале времени:
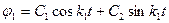при ; (4. 16)
при . (4. 17)
Для определения постоянных интегрирования необходимы четыре условия. Два из них отражают равенства углов поворота и угловых скоростей маятника в нижней точке (при 
):
; 
. (4. 18)
Запишем еще два соотношения
; 
, (4. 19)
в которых 
- некоторое, пока неизвестное число. Из (4. 19) следует, что при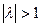 
должно иметь место увеличение колебаний маятника, а при 
- уменьшение.
Подставив (4. 16) и (4. 17) в (4. 18) и (4. 19), получим систему из четырех алгебраических уравнений относительно постоянных интегрирования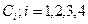 
. Условием наличия ненулевого решения является равенство нулю ее определителя, представляющего собой квадратное уравнение относительно :
, (4. 20)
где 
. Решив (4. 20), получим:
|
|
|
.
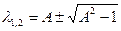Для того, что бы корни были действительными, необходимо выполнение условия
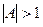(т. е. либо 
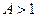, либо 
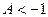); (4. 21)
при этом в первом случае 
, а во втором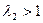 
. Отсюда следует, что выполнение неравенства (4. 21) является не только условием действительности корней уравнения, но и условием возникновения параметрического резонанса.
Условие 
определяет границу области параметрического резонанса; при 
корни 
, а период параметрических колебаний равен 
, при 
корни 
, а период колебаний равен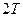 
. Введем обозначения:
; 
; 
; 
,
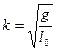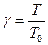где 
и 
- собственные частота и период колебаний маятника при его постоянной длине 
, 
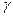- отношение периодов соответствующих колебаний, 
- глубина модуляции изменяющегося параметра.
Подставив введенные обозначения в (4. 21), получим соотношение
. (4. 22)
Легко убедиться, что при стремлении глубины модуляции к нулю соотношение (4. 22) принимает вид 
. Это условие выполняется при 
, то есть кривые границ областей параметрического резонанса на плоскости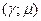 
будут пересекать ось 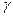в точках
На рисунке 4. 7 не заштрихованные зоны ( 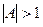) соответствуют областям параметрического резонанса. Границы областей параметрического резонанса около точек 
соответствуют значению и периодическому решению с периодом 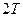, а около точек 
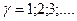, значению и периодическому решению с периодом .
Рис. 4. 7
Для задачи о раскачивании маятника одним из допущений было условие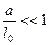 
(малость глубины модуляции ), поэтому на рисунке 4. 7 следует рассматривать лишь нижнюю, сравнительно узкую, полосу диаграммы.
Заметим, что все математические вычисления для получения областей неустойчивости были сделаны без допущения о малости глубины модуляции, поэтому они могут быть применены для аналогичных задач при значениях 
.
|
|
|
Диаграмма показывает, что, во-первых, областей параметрического резонанса оказалось бесконечно много, во-вторых, параметрический резонанс возможен в диапазонах 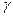, расположенных около значений . Отмеченные особенности отличают параметрический резонанс от резонанса в случае вынужденных колебаний, который возникает при совпадении собственной частоты с частой возмущающего силового воздействия.
|
|
|
