 |
4.5. Влияние вязкого трения на параметрические колебания.
|
|
|
|
4. 5. Влияние вязкого трения на параметрические колебания.
Рассмотрим влияние линейно-вязкого трения на колебательный процесс, описываемый с помощью уравнений Мейснера и Матье. Начнем с уравнения Мейснера, которое при наличии вязкого трения описывается уравнением
; 
,
где 
- коэффициент вязкого трения; 
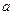- обобщенный коэффициент инерции. Построим матрицу переноса
Матрица 
строится для уравнения
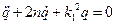, где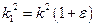 
. (4. 7)
Построим решение этого уравнения на интервале 
, где 
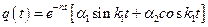(4. 8)
Используя начальные условия: 
: 
, 
, можно найти коэффициенты первого столбца матрицы переноса
; 
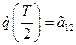. (4. 9)
Для этого продифференцируем решение (4. 8)
,
Тогда из начальных условий следует
,
кроме того, полагаем 
. В результате находим значение первой постоянной интегрирования
.
Окончательно решение и выражение для скорости записываются в виде
,
,
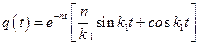Используя соотношения (4. 9), находим коэффициенты первого столбца матрицы переноса
,
,
Построим решение дифференциального уравнения (4. 7) на интервале при начальных условиях: : 
, 
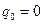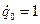
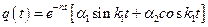(4. 10)
И соответственно для скорости
Коэффициенты второго столбца матрицы переноса определяются выражениями
|
|
|
; 
. (4. 11)
Положим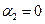 
, тогда из начальных условий следует 
и далее 
. Поэтому решение уравнения и выражение для скорости запишутся в окончательном виде так:
,
,
а коэффициенты второго столбца матрицы переноса будут равны
,
.
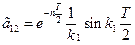Таким образом, матрица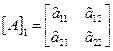 
построена. Перейдем к построению матрицы 
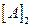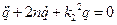. Уравнение движения для интервала запишем в виде
, где 
. (4. 12)
Уравнения (4. 7) и (4. 12) идентичны и отличаются лишь значениями коэффициентов 
и 
. Поэтому элементы матрицы 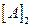могут быть получены из элементов матрицы путем замены коэффициентов на коэффициенты
;
;
;
.
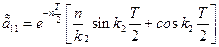Наконец и матрица 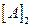построена. Дальнейшие расчеты без компьютера провести невозможно.
Выводы:
Расчеты, осуществленные с помощью компьютерной техники, показывают, что демпфирование лишь несколько увеличивает области устойчивости, но не ограничивает амплитуду колебаний в областях неустойчивости (области параметрического резонанса). Если считать демпфирование нелинейным, то колебания в области параметрического резонанса могут оказаться ограниченными.
4. 6. Учет вязкого трения в уравнениях Матье.
При рассмотрении параметрических колебаний, описываемых уравнениями Матье, возникает необходимость оценить влияние линейно-вязкого трения на амплитуду колебаний в областях параметрического резонанса. Рассмотрим этот вопрос подробнее. Уравнение Матье записывается в виде
. (4. 13)
Для оценки характера изменения амплитуды колебаний по истечении периода построим матрицу переноса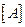 
. Проинтегрируем численно уравнение (4. 13) на интервале 
при начальных условиях : , . Заметим, что при интегрировании нельзя шаг выбирать автоматически. В результате находим
|
|
|
; 
.
Изменяя начальные условия : 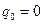, , 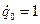повторим процедуру интегрирования, после чего найдем
; 
.
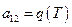Таким образом, матрица переноса 
построена. Повторяем эту процедуру число раз кратное периоду, затем вычисляем Евклидову норму матрицы 
,
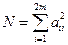где 
- число шагов умножения. После этого производим оценку устойчивости движения колебательной системы:
4. 
- неустойчивое движение;
5. 
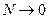- устойчивое движение;
6. 
- граница раздела между областями устойчивого и неустойчивого движения (периодический режим). Как и для уравнения Мейснера, условие существования периодического режима записывается в виде
.
Вывод: линейно-вязкое трение не ограничивает амплитуды параметрических резонансов (возможно ограничение амплитуд при учете нелинейного трения). Области устойчивости при наличии линейного вязкого трения расширяются.
|
|
|
