Управление транспортно-перегрузочными процессами.

Понятие об АСУ ТСК

Процессами

Для практической реализации и достижения высокого экономи­ческого эффекта при создании АСУ ТСК необходимо руководство­ваться следующими научными принципами: оптимальность,

системный подход и д е к о м и о з и ц и я. Сущность перво-го принципа состоит в том, что оперативные планы работы, которые разрабатываются ЭВМ, должны обеспечивать получение наилучших технико-экономических показателей; повышение производительнос­ти труда и значительную экономию трудовых ресурсов; существенное улучшение использования грузоподъемности и вместимости транспор­тных средств; снижение эксплуатационных затрат и т. д.

ТСК тесно взаимодействует с цехами и производственными уча­стками, с соседними железнодорожными станциями. Кроме того, АСУ ТСК является элементом АСУ транспортного цеха предприя­тия, железнодорожной станции, транспортного узла. Между транс­портными объектами и ТСК имеет место постоянное технологичес­кое взаимодействие. Все это обосновывает необходимость обеспечения системного подхода при создании АСУ, и прежде всего при построении экономико-математических моделей планиро­вания и управления ТСК: при разработке унифицированной системы кодирования, учитывающей интересы не только складского объекта, но и корреспондирующих с ним цехов предприятия, сосед­них станций, а возможно, и отрасли; при построении базы данных и информационного обеспечения, которые можно было бы эффек­тивно использовать в случае развития системы АСУ и др.

В рамках АСУ ТСК на различных уровнях управления решаются десятки различных оперативно-технологических задач, которые содержат сотни управляемых параметров.

Реализация глобальной экономико-математической модели оперативного планирования и управления ТСК, которая связывает управляемые параметры, целевую функцию и сопровождающие ее ограничения, весьма затруднительна.

Для решения такой многоразмерной задачи требуется немало времени, что нарушает оперативный режим планирования и его эффективность. Не все задачи связаны общими параметрами управления, поэтому целесо-

 

 

 

гласованности. При упомянутых ограничениях координирующие воздей­ствия могут изменяться в определенной области.

Оптимизация оперативного планирования работы ТСК осуществля-ется в такой последовательности:

• содержательное описание задач и их математическая формулировка;

• выявление функциональной зависимости и информационных свя­зей между отдельными подпроцессами и отвечающими им задачами;

• синтез глобальной экономико-математической модели;

• расчленение, декомпозиция (для упрощения расчетов) этой моде-

ли на отдельные блоки с учетом обеспечения межуровневого согласования;

• построение и отработка алгоритма программы решения задач на ЭВМ.

Экономико-математические модели, которые используют для реше­ния оптимизационных задач оперативного планирования ТСК, разде­ляют на следующие основные типы в зависимости от числа решаемых задач — на глобальные и локальные, от характера управляемых про­цессов — на детерминированные и стохастические, от количества уров­ней управления системой — одно- и многоуровневые, от применяемых методов решения задач — на аналитические и имитационные, от числа критериев оптимальности — многоцелевые и одноцелевые. Кроме того, экономико-математические модели в зависимости от применяемых кон­кретных математических методов разделяют на модели математичес­кого программирования, вариационные, эвристические, сетевые и т. д. Встречаются модели, которые строят с применением нескольких мате­матических методов.

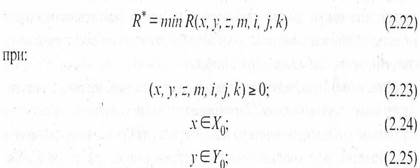В векторной форме модель оптимального оперативного планирования ТСК записывается следующим образом.

R* - min R(x, у, г, /;?, /, /, к) (2.22)

 

при:

 

(.v, v, г, т, /, j, к) > 0; (2.23)

xex,i (2.24)

>-eF_n; (2.25)

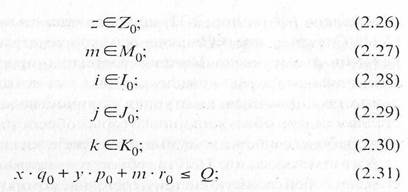
--GZ₀; (2.26)

шЕМ_п; (2.27)

о

•

/e/_ft:. (2.28)

'0

уел; (2.29)

кЕК₀; (2.30)

х ■ с/₀ + у • Pq + т • /'₀ < Q: (2.31)

 

где х, у —векторы, выражающие соответственно количество груженых и порожних вагонов различных типов, распределяемых по грузовым пунктам; вектор количе­ства распределяемых ПТМ или поточных транспортных линии различных типов; количество автомобилей и других средств напольного транспорта различ­ных типов, распределяемых на грузовых пунктах: Х₍₎. Y_{) и Л/₀ — векторы, представляющие собой соответственно общее количество груженых и порожних ва­гонов, автомобилей и средств напольного транспорта, ожидающих на ТСК момента обслуживания; Z₀—общее количество ПТМ и поточных т шип, которые могут быть задействованы для выполнения грузовых и складских операций: i—вектор, выража­ющий число используемых приоритетов при планировании обслуживания транспорт­ных потоков: j— вектор числа грузовых фронтов на ТСК. которые обслуживаются при подаче и уборке вагонов с одного рейса; к — вектор количества грузополучателей. которым доставляются грузы (комплектующих изделий), транспортным сред­ством с одного рейса; I₀. J₀, K₀ — соответственно векторы общего количества воз-можных приоритетов, грузовых фронтов и грузополучателей: Q —количество груза. Поясним смысл ограничений.

Условие (2.23) очевидно и не требует пояснений, условия (2.24) — (2.27), (2.29), (2.30) выражают ограничения по использованию соответствующих ресурсов, а также грузовых фронтов и грузополучателей; условие (2.28) уточняет фактическое использование имеющихся при­оритетов. Неравенство (2.31) требует соответствия необходимой и име­ющейся в наличии перерабатывающей способности грузовых пунктов. В этом условии q_,p₀ и r₍₎— соответственно средние загрузки груже­ных и порожних вагонов и автомобилей. Задача (2.22) — (2.31) формулируется так: необходимо найти такие параметры управления x* y* z* т * i* j* и k* которые бы доставили мини-

 

мум целевой функции (2.22) при соблюдении ограничений (2.23) — (2.31). Отметим, что перечисленными параметрами управления не ог­раничивается их число. Например, при планировании рейса стеллаж­ного крана-штабелера-комплектовщика в качестве своеобразного обоб­щенного параметра выступает количество и размещение ячеек стеллажей, при обслуживании которых обеспечивается минимум вре­мени рабочего цикла или суммарный пробег складской машины.

Уже отмечалось, что ТСК как объект планирования и управления представляет собой сложную систему, состояние которой определяется значи­тельным числом внешних 11 внутренних факторов. Это приводит к необхо­димости применения математических методов для выбора наилучшего варианта организации перевозок с участием железнодорожного и других видов транспорта. Использование математических методов оптимизации позволяет учесть развитие и техническое состояние всех элементов ТСК, параметры технологических процессов, объемы перевозок, грузопотоки и другие характеристики распределяемых ресурсов и выполняемых опера­ций и охватить весь процесс перевозок от прибытия грузов до вывоза их грузополучателем или передачи на другой вид транспорта.

Рассмотрим постановку задачи комплексного оптимального плани­рования и управления перевозками грузов с участием различных видов транспорта в ТСК.

Работа ТСК представлена в виде совокупности взаимосвязанных технологических операций, каждая из которых выполняется только од­ним из видов транспорта. Известны объемы перевозок грузов, которые должны быть осуществлены в течение заданного периода, и размеры ресурсов (людей, вагонов, автомобилей, ПТМ и др.), которые могут быть использованы для выполнения перевозок. При этом часть ресурсов спецанализирована для конкретного вида транспорта, а остальные ресурсы могут быть использованы на всех видах транспорта для выполнения любой из комплексных технологических операций.

Для формализации поставленной задачи предложена математичес­кая модель планирования и управления работой ТСК в оперативном плановом периоде.

Каждая из отраслевых технологических операций в этой модели описывается областями допустимых значений входных и выходных

параметров и некоторым оператором, связывающим соответствующие области. Это позволяет построить математическую модель в виде блоч­ной системы операторных неравенств и сформулировать задачу управ­ления работой ТСК в виде задачи математического программирования, которая хорошо интерпретируется в терминах планирования работы разных видов транспорта.

Каждая технологическая операция в ТСК может быть задана трой-

кой математических объектов:

(jr,.,G,.,^el,S, (2.32)

где, X_t Е Rⁿ", }JE R"¹, G, (Х_}) —> Y_h /El, S, причем Ж,- и К—некоторые множа-ства пространств R'¹" и R'" имеющих размерности т и iif G- —оператор, действую­щий на Х_г

Естественные ограничения, присущие каждой технологической опе­рации, определяют на множествах X_i и Y. V,-E1,S некоторые подмноже­ства, так что переменные, задающие эту операцию, оказываются связан­ными функциональными неравенствами вида Gf(xj)^b, где6,-Е/?^/7/ — фиксированные векторы V,«El, S,.y; EJ^,,

Общую математическую модель ТСК можно записать в виде системы функциональных неравенств, имеющих блочнодиагональную структуру:

*

%£ V *Ч э• *• з*\v /......... Ч

G_x{x_x).........<;/;,

G₂(x₂)...... ^b₂

-

(2.33)

• • • • ■ • •

GAx,-)*b_s

 

В этой модели Q и С, /El, 5", обозначают соответственно оператор, отражающий взаимосвязи между технологическими операциями, и опе­раторы, связывающие входные и выходные параметры каждой из 5 от­раслевых технологических операций /El, 5.

Под Xi; понимается вектор интенсивностей технологических спосо­бов отраслевых технологических операций i. При этом под технологическим способом понимается принятое сочетание производственных факторов (вагоны, автомобили, ПТМ и др.), которые могут участвовать

 

 

 

в отраслевой технологической операции в количествах, определяемых технологией организации работы в ТСК.

Таким образом, х = (Xi,..., Xim), где, например х_i — интенсивность использования первого технологического способа, т. е. определенной этим способом совокупности людских ресурсов, вагонов, ПТМ и др., позволяющих, в единицу времени осуществить определенные объемы перевозок и грузовых работ в ТСК, х_i2 — интенсивность использова­ния технологического способа и т. д. Вектор q в общем случае представляется в виде(q= (q1,q2,...,qn)^T, где здесь Т — знак транспонирования.

Компоненты этого вектора могут задавать как ограничения по ре­сурсам, так из здания по перевозкам грузов.

Например, определяет имеющиеся в ТСК трудовые ресурсы, специализированные по видам транспорта,объемы грузовых работ, которые могут быть выпол­нены в рассматриваемом периоде кранами, не специализированными по видам транспорта, и т. д.

Вектор B= {Bi1..... Bim) где Bi1 —количество технических средств

вида транспорта, осуществляющего 1-ю технологическую операцию (для железной дороги — это количество вагонов, локомотивов и др.); Bi1 — количество трудовых ресурсов, участвующих в 1-он технологической операции; B_i3 — производственные емкости складов, относящиеся к ни технологической операции, и т. д.

С достаточной для практических рас-четов точностью нелинейные взаимосвязи между отраслевыми техно­логическими операциями на разных видах транспорта в ТСК могут быть аппроксимированы линейными зависимостями, так что оператор Q мож­но считать линейным.

 

Для отдельных видов транспорта взаимосвязи между технологи­ческими способами в рамках каждой отраслевой технологической операции могут быть аппроксимированы линейными зависимостя­ми так, что операторы билинейны, причем Аi известные матрицы, столбцы которых описывают технологические способы ни отрасле­вой технологической операции.

Предполагается также, что компо­ненты вектора q являются значениями только общих ресурсов (подлежащих распределению диспетчером ТСК), а задания по перевозкам

 

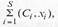грузов для отдельных видов транспорта являются соответствующи­ми компонентами векторов b_i.. Принято, что эффективность планирования работы отдельных видов транспорта математически описывается линейными функционалами вида (Сi., хi), где Ci, —стоимостная оценка затрат, связанная с исполь­зованием технологического способа работы 1-го вида транспорта, а эффективность работы в целом определяется как суммарная эффек­тивность планирования работы ТСК математически и описывается

линейным функционалом вида 2 (Q.a;), который в рассматривае-

мой задаче планирования требуется минимизировать на множестве допустимых планов работы ТСК.

Математическая формулировка рассматриваемой задачи планирова-ния и управления перевозкой грузов в ТСК с учетом принятых условий такова:

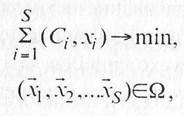
где Q — множество допустимых решений системы ограничении математической модели работы ТСК.

Это задача программирования большой размерности. Рассмотрен­ный ниже метод решения задачи планирования и управления различ­ными видами транспорта позволяет преодолеть вычислительные труд­ности, связанные с большой размерностью.

Исходная задача разбивается на локальные задачи по видам транс­порта и координирующую задачу диспетчера ТСК.

Локальные задачи ставятся так:

 

 

 

 

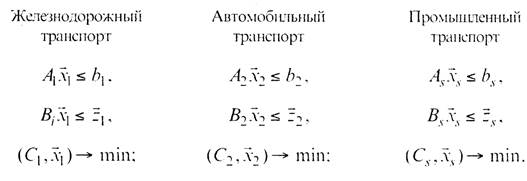Поиск оптимального плана работы представляет собой процедуру последовательного решения задач, двойственных к сформулированным локальным задачам и координирующей задаче диспетчера ТСК. в ходе которого происходит согласование «возможностей» отдельных техно­логических операций и «интересов» в целом. Эта процедура в боль­шинстве случаев является сходящейся, что позволяет после нескольких операций оборвать счет, когда изменение двойственных оценок становится меньше заданной величины е. т. е. когда некоторой ите­рацией с номером К будет установлено, что

 

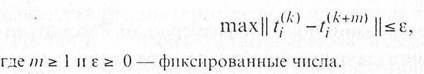Таким образом, решение задачи комплексного планирования уп­равления работой разных видов транспорта в ТСК удается разделить на решение задач планирования и управления работой отдельных ви­дов транспорта и координирующей задачей их взаимодействия в узле.

Содержательная интерпретация предложенного метода решения задачи планирования и управления грузовыми перевозками с учас­тием разных видов транспорта в ТСК такова.

Каждая отраслевая технологическая операция, отражающая ра-боту одного вида транспорта, выполняется с использованием опре­деленного количества специфических для этой операции людских и технических ресурсов: вагонов, локомотивов и т. п. для железно­дорожного транспорта; автомобилей, топливных ресурсов и т. п. для автомобильного транспорта и т. д.

 

Из изложенного выше можно сделать следующие выводы:

1. Совершенствование управления перевозочным процессом в ТСК при взаимодействии автомобильного, железнодорожного, водного и других типов транспорта является важным резервом ускорения до­ставки грузов, снижения непроизводительных затрат общетранспор-тных ресурсов, сокращения простоев автомобилей, вагонов и судов.

2. Важнейшими направлениями улучшения работы ТСК являются:

• комплексное планирование перевозок с участием разных ви­дов транспорта;

• автоматизация процессов управления, механизация погрузочно-разгрузочных работ на основе внедрения микроэлектроники, ро­ботов и робототехники:

• совершенствование оперативного планирования и управления ра­ботой автотранспорта при централизованном ввозе и вывозе грузов:

• развитие полного транспортно-экспеднционного обслуживания промышленных предприятий.

3. Оптимизация транспортных процессов в ТСК достигается на основе решения общетранспортной математической модели по кри­терию наилучшего использования имеющихся ресурсов и с приме­нением методов линейного программирования.

 

 

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: