 |
Элементы теории вероятностей и математической статистики
|
|
|
|
Элементы теории вероятностей и математической статистики
Теория вероятностей занимается исследованием вероятностных закономерностей массовых однородных явлений, многие её практические приложения используются в математической статистике.
Основным интуитивным понятием классической теории вероятностей является случайное событие. События, которые могут произойти в результате опыта, можно подразделить на три вида:
а) достоверное событие – событие, которое всегда происходит при проведении опыта (при броске игральной кости достоверным событием является выпадение числа очков не превышающего 6);
б) невозможное событие – событие, которое в результате опыта произойти не может(при броске игральной кости невозможным событием является выпадение 10 очков);
в) случайное событие – событие, которое может либо произойти, либо не произойти (при броске игральной кости случайным событием является выпадение 3 очков).
Операции над событиями.
1. Событие C называется суммой A+B, если оно состоит из всех элементарных событий, входящих как в A, так и в B. Сумма произвольного количества событий состоит из всех элементарных событий, которые входят в одно из Ai, i=1, ..., m.

2. Событие C называется произведением A и B, если оно состоит из всех элементарных событий, входящих и в A, и в B. Произведением произвольного числа событий называется событие состоящее из элементарных событий, входящих во все Ai, i=1, ..., m.
 |
3. Разностью событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.
 |
4. Событие называется противоположным событию A, если оно удовлетворяет двум свойствам.
|
|
|
Формулы де Моргана: 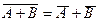 и
и 
 |
5. События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания.
События A и B называются несовместными, если они не имеют общих элементарных событий.
C=A× B=V
Тут V - пустое множество.
Классическое определение вероятности
При изучении случайных событий возникает необходимость количественно сравнивать возможность их появления в результате опыта. Поэтому с каждым таким событием связывают по определенному правилу, некоторое число, которое тем больше, чем более возможно событие. Это число называется вероятностью события и является вторым основным понятием теории вероятностей.
Пусть число возможных исходов равно п, а при т из них происходит некоторое событие А (число благоприятных исходов), тогда
Определение: Вероятностью события А называется отношение числа исходов опыта, благоприятных этому событию, к числу возможных исходов:
 - классическое определение вероятности.
- классическое определение вероятности.
Свойства вероятности
Свойство 1. Вероятность достоверного события равна единице.
Р(А) = 1.
Свойство 2. Вероятность невозможного события равна нулю.
Р(А) = 0.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
0 < Р(A) < 1.
Пример: Решить задачу:
В группе 15 студентов. Из них 8 юношей, 7 девушек. Какова вероятность выхода из кабинета девушки Р1(А), какова юноши Р2(А)?
Решение:
Пусть n – (число возможных исходов) –количество студентов в группе, тогда n=15
m1=7 - число благоприятных исходов выхода девушек;
m2=8 - число благоприятных исходов выхода юношей;
Вероятность выхода девушек из кабинета:
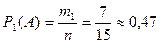
Вероятность выхода юношей из кабинета:

Ответ: Р1(А)=0, 47 Р2(А)=0, 53
Задание 1: Решить задачу:
Задача 1: В ясельной группе 8 девочек и 5 мальчиков. Какова вероятность уснуть первой девочке?
|
|
|
Задача 2: На автобусной остановке стоят 24 человека. 15 человек стоят в куртках, а остальные в пальто. Какова вероятность, что в автобус первым зайдёт человек в пальто?
Задача 3: В мешке 35 яблок. 2 зелёных и 33 красных. Какова вероятность вытащить первым зелёное яблоко?
|
|
|


