Дискретные случайные величины.

Дискретные случайные величины.

Для задания дискретной случайной величины нужно знать ее возможные значения и вероятности, с которыми принимаются эти значения. Соответствие между ними называется законом распределения случайной величины. Он может иметь вид таблицы, формулы или графика.

Таблица, в которой перечислены возможные значения дискретной случайной величины и соответствующие им вероятности, называется рядом распределения:

 

xi	x1	x2	…	xn	…
pi	p1	p2	…	pn	…

 

Графически закон распределения дискретной случайной величины можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами (x_i, p_i).

  x₁ x₂ x₃ x₄ x₅

Математическое ожидание случайной величины

 

Определение: Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности:

                           М(Х) = х₁р₁ + х₂р₂ + … + х_пр_п.                                         

Если число возможных значений случайной величины бесконечно, то

Пример 1: Найти математическое ожидание величины Х, заданной законом распределения

Х
Р	0, 2	0, 1	0, 4	0, 58

Решение:

М(Х)= х₁р₁ + х₂р₂ + х₃р₃ + х₄р₄ =2∙ 0, 2+3∙ 0, 1+5∙ 0, 4+8∙ 0, 58=7, 34

Ответ: М(Х)=7, 34

Задание 1:

Найти математическое ожидание величин, заданных законом распределения:

1)

Х
Р	0, 1	0, 2	0, 4	0, 67	0, 8	0, 8

 

2)

Х
Р	0, 12	0, 3	0, 5	0, 7

 

Свойства математического ожидания

 

1) Математическое ожидание постоянной равно самой постоянной:

М(С) = С.

2) Постоянный множитель можно выносит за знак математического ожидания:

                      М(СХ) = С М(Х).                                                        

Определение: Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.

 

Определение: Назовем произведением независимых случайных величин Х и Y случайную величину XY, возможные значения которой равны произведениям всех возможных значений Х на все возможные значения Y, а соответствующие им вероятности равны произведениям вероятностей сомножителей.

 

3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M(XY) = M(X)∙ M(Y)                                                       

 Определение: Определим сумму случайных величин Х и Y как случайную величину Х + Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин – произведениям вероятности одного слагаемого на условную вероятность второго).

4) Математическое ожидание суммы двух случайных величин ( зависимых или независимых ) равно сумме математических ожиданий слагаемых:

                   M (X + Y) = M (X) + M (Y)

Задание 2: Найти  математическое ожидание  суммы и произведения случайных величин Х и Y, заданных своими законами распределения:

Х
Р	0, 1	0, 3	0, 5

 

Y
Р	0, 3	0, 2	0, 6

 

Дисперсия

 

Определение: Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:

                                       D(X) = M (X – M(X))².                                                

Замечание 1. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.

Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии:

D(X) = M(X ² ) – M ² (X)

Свойства дисперсии

1) Дисперсия постоянной величины С равна нулю:

                                 D (C) = 0.                                                                  

2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

D(CX) = C² D(X)

3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:

                                      D(X + Y) = D(X) + D(Y).                                     

4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

                                  D(X – Y) = D(X) + D(Y).                                                     

Среднее квадратическое отклонение

Определение: Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:

                                        .                                                        

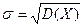Пример 1: Вычислить дисперсию и среднее квадратическое отклонение величины, заданной своей таблицей распределения:

Х
Р	0, 1	0, 3	0, 5

Решение:

Вычислим математическое ожидание М(Х)

М(Х)= 2∙ 0, 1+3∙ 0, 3+5∙ 0, 5=0, 2+0, 9+2, 5=3, 6

Вычислим математическое ожидание М(Х²)

М(Х²)= 2²∙ 0, 1+3²∙ 0, 3+5²∙ 0, 5=0, 4+2, 7+12, 5=15, 6

Подставим М(Х) и М(Х²) в формулу для дисперсии:

D(X) = M(X ² ) – M ² (X)=15, 6-(3, 6)²=15, 6-12, 96=2, 64

Подставим D(X) в формулу для среднего квадратического отклонения

=1, 62

Ответ: D(X)=2, 64, σ =1, 62

  Задание 1: Вычислить дисперсию и среднее квадратическое отклонение величины, заданной своей таблицей распределения:

 

Х
Р	0, 2	0, 3	0, 4	0, 6

 

Задание 2: Вычислить сумму и разность дисперсий Х и Y, а также найти их квадратическое отклонение:

1)

 

Х
Р	0, 2	0, 4	0, 1

 

Y
Р	0, 1	0, 4	0, 5

2)

 

Х
Р	0, 1	0, 2	0, 5	0, 9

 

Y
Р	0, 3	0, 1	0, 12	0, 4

 

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: