 |
Основные формулы комбинаторики
|
|
|
|
Основные формулы комбинаторики
При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества.
Перестановки
Определение Перестановки – это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения.
Число всех возможных перестановок:
Рп = п! (n факториал)
п! =1∙ 2∙ 3∙ 4∙ ……. ∙ n
Пример1: Вычислить 7!
Решение:
7! = 2· 3· 4· 5· 6· 7 = 5040
Ответ: 7! = 5040
Пример2: Вычислить 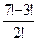
Решение:

Ответ: 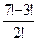 =2517
=2517
Задание 1: Найти ошибку:
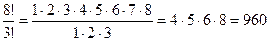
Задание 2: Вычислить:
1)  4)
4) 
2) 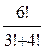 5)
5) 
3) 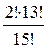 6)
6) 
7) 
Пример 3: Упростить:

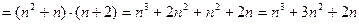
Задание 3: Упростить
1)  2)
2)  3)
3) 
4) 
Размещения
Определение: Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком.
Число всех возможных размещений
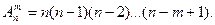
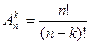
Пример1: Вычислить 


Задание 1: Вычислить
1) 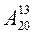 2)
2) 
2)  3)
3) 
Пример 2: Решить задачу:
В группе студентов 15 человеке. Формируется бригада из 4 человек для участия в олимпиаде по математике. Какое число вариантов возможно?
Решение:

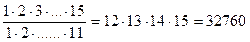
Ответ: 32760 вариантов.
Задание 2: Решить задачу:
|
|
|
Задача 1: В ясельной группе из 13 человек требуется выбрать 4 человек для чтения стихов на утреннике, посвящённому Дню защиты детей. Сколькими способами это можно сделать?
Задача 2: На остановке стоят 24 человека. 13 из них собираются ехать на троллейбусе, остальные на автобусе. Какое количество вариантов собрать группу из людей стоящих на остановке, которая поедет в автобусе?
Задача 3: Какое количество вариантов выбрать из мешка с 35 яблоками 21 зелёное?
Сочетания
Определение: Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов).
Число сочетаний
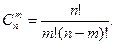
Пример 1: Вычислить 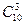

Задание 1: Вычислить
1) 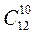 2)
2) 
3)  4)
4) 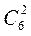
Пример 2: Решить задачу
В студенческой группе из 15 человек требуется найти пару учащихся для поощрения стипендией. Какое количество сочетаний возможно?
Решение:
 вариантов
вариантов
Ответ: 105 вариантов
Задание 2: Решить задачу:
Задача 1: В ясельной группе из 13 человек нужно выбрать 3-х человек для наблюдения за остальными детьми, чтобы они не ели зубную пасту в ванной комнате. Какое количество сочетаний возможно?
Задача 2: Из стоявших на остановке 24 человек нужно выбрать 6-х, которые не влезут в маршрутное такси. Какое сочетание людей возможно?
Задача 3: Из мешка с 35 яблоками нужно выбрать пару яблок (зелёное и красное). Какое количество сочетание возможно?
Пример 3: Доказать, что
 +6
+6  +6
+6 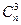 =n3
=n3
Решение:
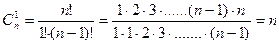

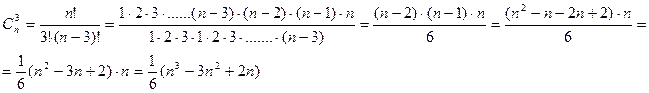
 +6
+6  +6
+6 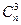 =n+6∙
=n+6∙ 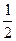 (n2-n)+6∙
(n2-n)+6∙  (n3-3n2+2n)= n+3n2-3n+n3-3n2+2n=n3
(n3-3n2+2n)= n+3n2-3n+n3-3n2+2n=n3
n3= n3
Задание 3: Доказать, что
1) 2  +
+  =n2
=n2
2) 6 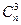 +6
+6  =n∙ (n2-1)
=n∙ (n2-1)
Теорема сложения вероятностей
Теорема 1 (теорема сложения): Вероятность Р(А + В) суммы событий А и В равна
Р (А + В ) = Р (А) + Р (В) – Р (АВ).
|
|
|
Пример 1: Решить задачу:
В группе студентов 9 блондинов, 4 брюнета и 2 лысых. Подсчитать вероятность выхода из кабинета человека с волосами на голове.
Решение:
Всего в группе 9+4+2=15 человек
Вероятность выйти блондину Р1= 
брюнету Р2= 
Тогда искомая вероятность Р= Р1+Р2= 
Ответ: Вероятность около 0, 87
Задание 1: Решить задачу:
В урне 3 белых шара, 2 синих, 1 красный, 5 жёлтых, 7 зелёных. Подсчитать вероятность выбрать цветной шар.
Теорема умножения вероятностей.
Определение: Назовем условной вероятностью р(В/А) события В вероятность события В при условии, что событие А произошло.
Теорема2 (теорема умножения): Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:
р (АВ) = р (А) · р (В/А).
Пример2: Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания при одном выстреле равны соответственно 0, 6 и 0, 7. Какова вероятность того, что при однократном выстреле стрелков цель будет поражена?
Решение:
Вероятность промахов стрелков: первого 1-0, 6=0, 4
второго: 1-0, 7=0, 3
имеем: Р=1-0, 4∙ 0, 3=1-0, 12=0, 88
Ответ: вероятность Р=0, 88
Задание 2: Решить задачу:
В ясельной группе доедают кашу 1 девочка и 1 мальчик. Вероятность того, что кашу доест девочка Рд=0, 43, мальчик Рм=0, 53. Какова вероятность того, сто каша будет доедена?
Формула Бернулли:
 . , где
. , где
n – число опытов А;
к – число наступления события А;
р- вероятность события А;
q – вероятность не наступления события А (q=1-р);
Пример 1: Решить задачу:
Какова вероятность того, что при 4 подбрасываниях игрального кубика число три появится ровно 2 раза.
Решение:
n = 4 (4 опытов (подбрасывания))
к= 2 (число наступления события (появления требуемого числа три))
Вероятность р=  (так как 6 граней в кубике)
(так как 6 граней в кубике)
Невероятность q= 1-  =
= 
Подставим в формулу Бернулли:
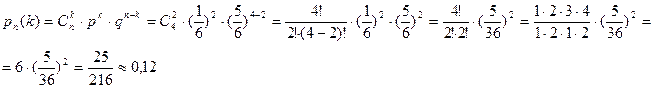 Ответ: Вероятность Р=0, 12
Ответ: Вероятность Р=0, 12
|
|
|
Задание 1: Решить задачу:
Задача 1: Какова вероятность того, что при 5 подбрасываниях игрального кубика число два появится ровно 3 раза?
Задача 2: Игральный кубик подброшен 10 раз. Найти вероятность выпадения единицы 7 раз.
Простейшие характеристики законов распределения:
· математическое ожидание
· дисперсия
· среднее квадратическое отклонение
Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины.
Определение: Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.
Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y, Z, …), а их возможные значения – соответствующими малыми буквами (xi, yi, …).
Случайные величины подразделяются на две группы: дискретные и непрерывные.
Определение: Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.
Определение: Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.
|
|
|


