 |
В) алгоритмы обработки при малом числе отсчетов, при нормальном законе распределения вероятности, обеспечение оптимального числа отсчетов при заданной неопределенности результата измерения.
|
|
|
|
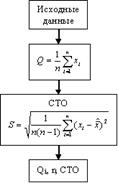Под обработкой результатов измерения подразумевается получение результата многократного измерения и установление его неопределенности. В простейшем случае при малом числе n и невозможности снесения поправок обработка начинается по следующему алгоритму.
Затем учитывается неопределенность, обусловленная дефицитом измерительной информации: определяется насколько истинное значение измеряемой величины может отличаться от действительного за счет влияющего фактора, точный учет которого невозможен. Выбирается закон распределения истинного значения на полученном интервале, т.е.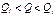 
и находится аналог дисперсии: 
. В остальных случаях обработка начинается с так называемого исправления результатов измерения. Оно состоит во внесении поправок, исключении ошибок. Результаты измерений не должны содержать ошибок, которые возможны из-за невнимательности оператора, описок, сбоев аппаратуры, толчков или ударов, перепадов напряжения в сети, кратковременных изменений условий и других причин, не связанных ни с какой статистической закономерностью.
Отсчеты в результате ошибок заметно отличаются от большинства. При нормальном законе распределения применяется правило 3-х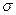 
, по которому без дополнительной проверки отбрасываются те отсчеты, которые отличаются от среднеарифметического больше, чем на 
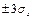, т.к. вероятность их случайного появления меньше, чем 0,003. Иногда по этому правилу проверяют min-ый и max-ый отсчеты.
Дальнейшей обработке подвергают результаты измерений, оставшиеся после исключения ошибок.
Вся априорная информация полностью содержится в законе распределения вероятности исправленных результатов измерения. Для этого определения строится гистограмма.
|
|
|
Ось абсцисс в соответствии с рекомендациями ГОСТа разбивается на единичные интервалы ΔQ, которые служат основаниями прямоугольников. Высота прямоугольников равна 
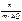, где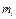 
- число результатов измерения, попавших в i-ый интервал. Получившееся ступенчатое распределение и называется гистограммой.
Масштаб гистограмм рекомендуется выбирать т.о., чтобы высота гистограммы относилась к ее основанию как 5 к 8. По виду гистограммы выдвигается гипотеза о том, какому закону распределения вероятности подчиняются результаты измерения. ГОСТ определяет рекомендуемое число интервалов для построения гистограммы:
| n | Число интервалов |
| 40-100 | 7-9 |
| 100-500 | 8-12 |
| 500-1000 | 10-16 |
| 1000-10000 | 12-22 |
Установленный закон распределения вероятности результатов измерения наиболее полно характеризует неопределенность, возникающую из-за случайного характера отсчета. А его композиция с законом распределения, учитывающая неопределенность результата измерения, обусловленную дефицитом информации, исчерпывающим образом отображает неопределенность результата.
Однако, пользоваться законом распределения вероятности на практике не всегда удобно. На практике почти всегда ограничиваются их числовыми характеристиками, хотя они и менее информативны.
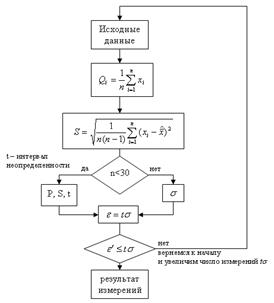
Автоматизация измерений и обработки их результатов позволяют оптимизировать количество отсчетов. Если, например, условием измерительной задачи требуется, чтобы истинное значение измеряемой величины с доверительной вероятностью Р не выходило за пределы заранее заданного доверительного интервала, то обработку результатов можно организовать по следующему алгоритму:
|
|
|
