Результаты вычислений с указанием меры его неопределенности.

Полный результат измерения должен содержать в себе оценку значения y выходной величины Y и значение расширенной неопределенности измерения U с указанием доли (coverage probability) p ожидаемых значений, которые могли бы быть обосновано ей (выходной величине) приписаны:Y=y+U, p=0.95

Данная запись буквально означает следующее: большая доля (95%) ожидаемых значений, которые могли бы быть обосновано приписаны к измеренной нами величине Y, находятся в интервале от (y – U) до (y + U).При этом надо иметь в виду, что нахождение измеренной величины Y внутри интервала имеет некую вероятность (не путать с заданной долей ожидаемых значений!), меньшую единицы, и, следовательно, попадание Y вне заданного интервала не исключено, хотя и маловероятно.

Трансформация закона распределения вероятности при вычислениях по формулам.

Часто неизвестные значения одних величин вычисляются на основании результатов измерения других. Распространенной ошибкой при этом является обращение с результатами измерений как с неслучайными величинами.

Простейшими являются вычисления по формуле Q=f(A), где f – известная ф-ия. Если А – результат измерения, то эта случайная величина подчиняется определенному з-ну распределения вероятности, а данное преобразование связано с трансформацией этого з-на. Плотность распределения вероятности Q выражается через плотность распределения вероятности А – P_A(A) и обратную ф-ию f^-1 согласно теории вероятности следующим образом:

Например, если результат измерения А – сторона квадрата и она подчиняется нормальному з-ну распределения вероятности 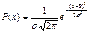, то плотность распределения вероятности площади квадрата:

Дисперсия результата вычислений.

При сложных функция f и з-нах распределения вероятности результатов измерения даже простейшие преобразования связаны со значительными математическими трудностями. В этом случае ограничиваются приближенными вычислениями на уровне моментов. Они основаны на разложении ф-ци f(А) в ряд в окрестности точки , тогда Этот способ становится фактически единственным, когда число переменных возрастает хотя бы до 2-х и более Q=f(A,B).

Дисперсию результатов вычислений в этих случаях м. записать:

,

где σ_x, σ_y – средние квадратические отклонения результатов измерения величин А и В;

R – смешанный центральный момент второго порядка совместного распределения случ. величин x и y.

Корреляция как мера линейной статической связи между двумя случайными величинами.

Величина 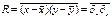и называется корреляцией. Он служит мерой линейности статистической связи между двумя случайными величинами и указывает на то, как связаны между собой случайные величины x и yи как они обнаруживают тенденцию к синхронному изменению.

Напр., увеличение случайных значений величины x сопровождается и некоторым увеличение или уменьшением случайных значений y. Обычно это происходит под влиянием какого-то общего фактора, напр. изменения температуры. В этом случае корреляционный момент R>0, а корреляцию между случайными величинами x и yназывают положительной.

Если связь между случайными величинами подчиняется 2-му графику, то говорят, что R<0.

Если значения, принимаемые величинами, статистически не связаны, то их корреляционный момент R=0. Такие величины называются некоррелированными.

На практике вместо смешанного центрального момента 2-го порядка м.б. вычислена его оценка:

Оценка дисперсии м.б. представлена:

В этом случае результаты вычислений д. сопровождаться указаниями величин:

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: