 |
Определение рациональных режимов резания
|
|
|
|
Разработка технологического процесса механической обработки завершается установлением технически обоснованных норм времени на каждую операцию. Чтобы добиться оптимальных норм времени, необходимо в полной мере использовать режущие свойства инструмента и технические возможности металлорежущего оборудования. Для этого определяются рациональные режимы резания на все операции механической обработки детали. Наилучшие результаты дает аналитический расчет режимов резания с помощью эмпирических зависимостей.
При выборе режимов обработки необходимо придерживаться определенного порядка, т.е. при назначении и расчете режимов резания учитывают тип и размеры режущего инструмента, материал его режущей части, материал и состояние заготовки, тип и мощность оборудования и т.д. Следует помнить, что элементы режимов резания функционально взаимосвязаны между собой.
Определение режимов резания начинают с описания исходных данных, куда входят: наименование и номер операции, содержание (структура) операции, операционный эскиз, технические требования на изготовления детали, паспортные характеристики оборудования, материал заготовки и его механические свойства, сведения об режущем инструменте (материал режущей части, стойкость). Для каждого перехода определяют глубину резания, подачу, скорость резания, частоту вращения, силу резания, крутящий момент и мощность резания.
Полученные режимы резания корректируются по паспортным данным станка и проверяются по мощности его электродвигателя. Необходимо, чтобы потребная мощность резания не превышала номинальную мощность электродвигателя оборудования.
В связи с тем, что аналитический расчет режимов резания является процессом довольно-таки трудоёмким, в курсовом или дипломном проекте таким методом определяются режимы резания на 1-2 операции по согласованию с руководителем проекта. Для остальных операций технологического процесса режимы резания определяются по нормативам режимов резания с учетом конкретных условий, то есть введением поправочных коэффициентов [85-88, 90, 105].
|
|
|
В связи с тем, что аналитический расчет режимов резания довольно широко освещен в литературе [1, 3, 61, 105], в данном учебном пособии он не приводится.
Нормирование технологических операций
Техническая норма времени на обработку заготовки является одним из основных параметров для расчета стоимости детали, количества металлорежущего оборудования, заработной платы рабочих, планирования производства.
Техническую норму времени определяют на основе технических возможностей станочного оборудования, технологической оснастки, режущего инструмента, схемы построения операции и переходов, автоматизации процесса обработки детали. В массовом производстве рассчитывается штучное время, в серийном и единичном – штучно-калькуляционное.
В курсовом или дипломном проекте для тех операций, режимы резания которых определялись расчетно-аналитическим путем, нормы времени определяются также расчетно-аналитическим методом [10, 61, 90, 101, 108]. Для остальных операций нормы времени выбираются по табличным данным [82-85, 87, 88]. Для станков с ЧПУ нормы времени выбираются из [85].
Расчет точности технологического процесса механической
Обработки детали
До недавнего времени расчет точности технологических процессов осуществлялся на основе методов построения и расчета размерных цепей, Однако в последнее время эти методы вытесняются более эффективными методами, основанными на построении и расчете графов технологических процессов.
|
|
|
Теория графов зародилась в 18 веке и получила свое развитие как отдельная отрасль математики во второй половине 30-х годов прошлого столетия, В настоящее время теория графов с успехом применяется в различных областях знаний для решения практических задач, Универсальность применения теории графов объясняется тем, что конкретные понятия при анализе их взаимной связи она абстрагирует и формализует,
Граф – это графическое изображение какой-либо замкнутой структуры.
Структура – совокупность элементов любой природы, связанных каким-либо образом (или способом) между собой.
Например, деталь - структура, т.к. имеет совокупность связанных между собой размерами поверхностей. Элементами структуры «деталь» являются поверхности и связи между ними. Связь можно установить только между поверхностями.
Структуру можно изобразить графически. Приведем конкретный пример. На рис.2.3 изображен эскиз детали, совмещенный с эскизом заготовки.

Рис. 2.3
Обработке подвергаются поверхности, расположенные по горизонтали. Поверхности 1 и 5 образуют заготовку, имеющую размер Н. На первом технологическом переходе заготовка устанавливается на поверхность 1 и у нее обрабатываются поверхности 4 и 3 c обеспечением размеров соответственно А1 и А2. На втором переходе заготовка устанавливается на поверхность 4 и у нее обрабатывается поверхность 2 в размер А3. Припуски на эскизе обозначены как z1, z2 и z3. Требуемые размеры детали обозначены через h1 и h2.
Поверхности 1 и 5 заготовки детали образуют структуру, так как связаны между собой размером H. Графически эту структуру можно изобразить в виде двух точек, отображающих поверхности 1 и 5, и отрезком прямой, соединяющим эти точки и отображающим размер Н.
Структурами являются также поверхности детали 1 и 4, 1 и 3, 2 и 3, так как они связаны соответственно операционными размерами А1, А2 и А3. Эти структуры также можно изобразить графически в виде точек, отображающих поверхности, и отрезками прямых, отображающих соответствующие размеры (рис. 2.4).

Рис.2.4
Если три из этих четырех структур, имеющих общую поверхность 1, объединить между собой, то получится две структуры – одна сложная и одна простая – рис.2.5.
|
|
|
Эти две структуры имеют общую поверхность 4. Поэтому эти две структуры можно также объединить, в результате чего получится одна полная структура, представлена на рис. 2.6.


Рис. 2.5
Назовем линии, отображающие размерные связи – ребрами, а точки, отображающие поверхности – вершинами.
Как видно, представленная на рис. 2.6 структура имеет количество ребер на единицу меньше числа вершин и притом все вершины связаны между собой единственным путем. Такая структура называется деревом.
В дальнейшем мы будем изучать деревья. Как и всякое дерево данное дерево имеет корень – поверхность, которую мы примем за начало при построении дерева (базовая поверхность на I-ом переходе).

Рис. 2.6
Если обработку детали вести в другой последовательности, то и дерево получается другим. Чтобы не ошибиться в правильности построения дерева, лучше поверхности изображать в виде кружочков, внутри которых проставляется номер поверхности (рис. 2.7). Ребра удобнее показывать в виде стрелок, причем стрелка должна быть направлена в сторону обработанной на данном переходе поверхности.
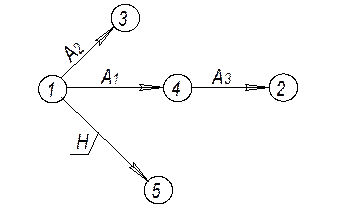
Рис. 2.7
Проверка правильности построения дерева: ко всем вершинам, кроме корня, находит только одна стрелка, к корню – ни одной.
Соединим свободные вершины дерева. Они связаны между собой величинами припусков и заданными по чертежу размерами. Заданные размеры детали обозначим круговыми стрелками, а припуски – зигзагообразными.
Направления стрелок, отображающих припуски и заданные размеры детали по чертежу выбираются произвольно. Получился граф. По существу, граф представляет собой размерную цепь, которую легко рассчитать.

Рис. 2.8
Чтобы не ошибиться в расчете, необходимо полностью абстрагироваться от чертежа детали. Для этого каждому размеру присваивают знак «плюс», если стрелка направлена от меньшего к большому номеру вершины, и знак «минус», если наоборот.
Далее четко сформулируем методику построения и расчета графа.
Исходные данные:
1. Чертеж детали с необходимыми размерами и допусками.
|
|
|
2. Эскиз заготовки.
3. Последовательность обработки поверхностей заготовки.
4. Технологические базы при обработке поверхностей.
5. Допуски на операционные размеры. Как правило, допуск на операционный размер должен соответствовать экономически достижимой точности на данной операции. Если за базу взята необработанная поверхность, то допуск увеличивается примерно в 1,5 раза по сравнению с экономически достижимым.
6. Минимальное значение припуска на обработку каждой поверхности.
Пример. Пусть для указанного выше случая дано: чертежные размеры детали - h1 = 80±0,2; h2 =2±0,3. По справочным данным выбираем экономически рациональные допуски на размер заготовки и на операционные размеры -  =1,6 мм;
=1,6 мм; 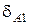 = 0,3 мм;
= 0,3 мм;  =0,2 мм;
=0,2 мм;  = 0,1 мм, а также на минимальные значения припусков - Z1 min = 1,8; Z2 min = Z3 min = 0,3 мм.
= 0,1 мм, а также на минимальные значения припусков - Z1 min = 1,8; Z2 min = Z3 min = 0,3 мм.
Порядок построения графа
1. Вычерчивается эскиз детали, совмещенный с эскизом заготовки. Разными буквами с соответствующими индексами обозначаются все заданные чертежом размеры детали, размеры заготовки, промежуточные припуски и операционные размеры.
2. В определенной последовательности (справа налево, слева направо, сверху вниз, снизу вверх, по часовой или против часовой стрелки и т.д.) каждой поверхности заготовки и обработанной поверхности присваивается порядковый номер 1, 2, 3 и т.д.
2. Строится дерево. Поверхность, используемая в качестве технологической базы на первом технологическом переходе первой технологической операции, выбирается в качестве корня дерева. Вершины дерева изображаются в виде кружочков, внутри которых проставляется номера соответствующих им поверхностей. Ребра показываются в виде стрелок, направленных в сторону обработанных на данном переходе поверхностей. Над ребрами указываются соответствующие им буквенные обозначения размеров заготовок и операционных размеров.
3. Осуществляется проверка правильности построения дерева: к корню не должно подходить ни одной стрелки, к другим вершинам – по одной стрелке, дерево не должно иметь ни разрывов, ни замкнутых контуров.
4. На дереве показываются круговыми стрелками размеры детали по чертежу и зигзагообразными стрелками припуски. Направление стрелок произвольное. Над круговыми и зигзагообразными стрелками указываются соответствующие им буквенные обозначения.
5. Под каждой стрелкой на графе проставляется знак «плюс», если стрелка направлена от вершины с меньшим к вершине с большим порядковым номером, и знак «минус» - если наоборот.
Построение графа удобно осуществлять в табличной форме. В табл. 2.9 приведено построение графа для рассмотренного примера на рис. 2.4.
|
|
|
Таблица 2.9
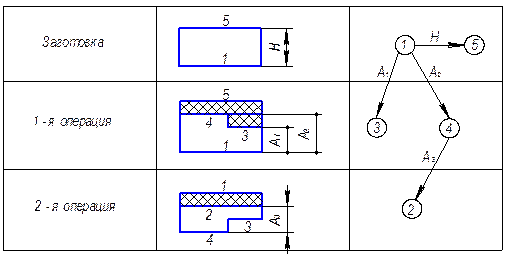
Последовательность расчета графа
1. Строятся уравнения допусков контуров графа. В качестве замыкающих размеров при расчете контуров графа используются чертежные размеры и размеры припусков.
Первыми рассчитываются контуры, которые имеют один размер детали, заданный чертежом, и операционные размеры. По заданным допускам на размеры детали уточняются допуски на операционные размеры. Если сумма допусков на операционные размеры не равна допуску на размер детали, то допуски на операционные размеры соответственно корректируются. Затем следует переходить к контурам, имеющим операционные размеры с уточненными допусками и один операционный размер или размер заготовки, допуск на который следует уточнить.
2. По известным допускам на размеры заготовок и на операционные размеры определяются допуски на припуски.
3. По заданным минимальным значениям припуска и рассчитанным допускам на припуски рассчитываются максимальные и средние значения припусков.
4. Составляются уравнения размеров контуров графа, на основе которых рассчитываются средние значения операционных размеров и средние размеры заготовки. Каждый из таких контуров должен содержать лишь один неизвестный операционный размер или размер заготовки.
5. При составлении уравнения контура следует придерживаться правила: если направление движения по контуру совпадает с направлением стрелки, то размер записывается с присвоенным ему на графе знаком, в противном случае знак меняется на обратный.
6. Окончательно устанавливаются номинальные операционные размеры, размеры заготовок и их отклонения. Номинальные значения операционных размеров должно быть таким, чтобы отклонения допусков отсчитывались в металл.
Расчет графа удобно производить в табличной форме. Чтобы пояснить методику расчета графа, произведем построение таблицы 2.10 для предложенного выше примера.
Табл.2.10
| № п/п | Уравнение контура | Обозна- чение р-ра | Допуск | Размер | Расчетный размер | ||
| мин. | сред. | макс. | |||||
| 1. | 
| h1 | 0,4 | 79,8 | 80,2 | 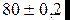
| |
| 2. | 
| h2 | 0,6 | 1,7 | 2,3 | 
| |
| 3. | 
| H | 1,6 | 84,95 | 85,75 | 86,55 | 
|
 4. 4.
| 
| A1 | 0,3 0,2 | 84,45 | 84,55 | 84,65 | 
|
 5. 5.
| 
| A2 | 0,2 0,1 | 82,5 | 82,55 | 82,6 | 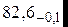
|
| 6. | 
| A3 | 0,1 | 81,95 | 82,05 | 
| |
| 7. | 
| Z1 | 1,8 | 0,2 | 1,1 | 2,0 | |
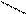 8. 8.
| 
| Z2 | 0,3 | 0,3 1,85 | 2,15 | ||
| 9. | 
| Z3 | 0,3 | 0,3 | 0,45 | 0,6 |
Имея перед глазами граф, строим уравнения допусков контуров. При этом помним, что чертежные размеры детали и размеры припусков являются замыкающими звеньями и поэтому равны сумме допусков составляющих звеньев контуров.
Построение начинаем с контура 1-3-4, так как он содержит один чертежный размер h2 и два операционных размера A1 и А2. Уравнение записываем в п. 1 таблицы 2.10. Как видно, допуск размера h2 больше суммы допусков размеров А1 и А2. Поэтому допуск на размер А1 или А2 можно увеличить по сравнении с допуском, взятым из справочника. Но прежде чем корректировать эти допуски построим уравнение допусков второго контура.
В качестве второго контура выбираем контур 1-3-2-4, так как он также имеет чертежный размер детали h1. Записываем уравнение в строке 2 табл. 2.10. В результате расчета устанавливаем, что допуск на размер h2 оказался меньше суммы допусков на размеры А1, А2 и А3. Следовательно, допуски на операционные размеры необходимо уменьшить. Принимаем решение, что допуск на размер А3 остается неизменным, а допуски на размеры А1 и А2 уменьшаем на 0,1. В табл. 2.10 против А1 и А2 аккуратно зачеркиваем табличные допуски и присваиваем им новые значения.
Так как чертежных размеров больше нет, то переходим к построению уравнений допусков контуров, содержащих размеры припусков. Контур 1-3-2 содержит припуск Z3. Уравнение допусков этого контура записываем в строке 3. табл.2.10. В результате расчета устанавливаем, что допуск на припуск Z3 равен 0,3. Записываем это значение в колонку 4 табл. 2.10 против буквенного обозначения Z3.
Подобным образом строим и рассчитываем уравнения допусков оставшиеся двух контуров 1-3-4 и 1-4-5, которые содержат припуски Z2 и Z1. Записываем эти уравнения в строки 4 и 5 табл. 2.10. В результате расчета устанавливаем допуски на припуски Z2 и Z1. Найденные значения припусков и записываем из значения в колонку 4 табл. 2.10 против этих буквенных обозначений.
Так как теперь известны допуски на припуски, а минимальные значения припусков мы взяли по справочным данным, то рассчитываем средние и максимальные значения припусков и записываем эти значения в колонки 6 и 7 табл. 2.10. Однако из графа следует, что припуск Z2 совпадает с чертежным размером h2 детали. Поэтому принимаем средний размер припуска равным среднему чертежному размеру h2. В результате этого корректируем его минимальный размер и записываем это новое значение в колонку 5.
На этом построение и расчет уравнений допусков контуров графа мы закончили. Теперь мы имеем не только чертежные размеры, но и размеры припусков. Остались неизвестными операционные размеры и размеры заготовки.
Для определения этих размеров переходим к построению и расчету уравнений размеров контуров. Начинаем построение с контура, который имеет один неизвестный операционный размер и известные чертежные размеры и размеры припусков. Таким контуром является 3-4-2. Он содержит неизвестный операционный размер А3 и известные размеры припуска Z2 и чертежный размер h1. Выбираем направление часовой стрелки. Так как направление стрелок Z2 и А3, составляющих контур, совпадает с направлением часовой стрелки, то эти размеры в уравнении размеров контура записываем со своим знаком, ранее проставленном на графе. Знак размера h1 меняем на противоположный. Уравнение записываем в строку 6 табл. 2.10. По известным средним размерам Z2 и h1 из этого уравнения находим средний размер А3 и записываем его в колонку 6 таблицы. Так как допуск на этот размер известен, то находим минимальный и максимальный размер А3 и записываем эти значения в колонки 5 и 7 табл. 2.10.
Далее из контура 1-4-2 по известным размерам Z3 и А3 находим размер А1. Соответствующее уравнение размеров контура записываем в строке 7. Так как направление стрелок размеров А1 и А3 совпадает с направлением часовой стрелки, то их в уравнении записываем со своим знаком. Направление стрелки Z3 противоположно направлению часовой стрелки. Поэтому знак «плюс» у этого размера при составлении уравнения размеров данного контура меняем на «минус». Находим средний размер А1 и записываем его в колонке 6. По известным среднему размеру и допуску находим предельные значения размера А1, которые записываем в колонки 5 и 7.
Подобным образом строим уравнения размеров контуров 1-3-4 и 1-5-4, находим операционный размер А2 и размер заготовки Н.
В соответствии с указанными выше рекомендациями заполняем колонку 8 табл. 2.10. На этом расчет графа заканчивается.
Достоинства графа:
1. Наглядность взаимосвязей размеров.
2. Простота построения графа и расчета размеров.
3. Возможность создать и использовать строгие алгоритмы при расчетах, унифицировать их.
4. Перспектива автоматизации процесса расчета.
5. Возможность оптимизировать технологический процесс изготовления изделий.
|
|
|


