 |
Оптимизация технологического процесса
|
|
|
|
Эффективность механической обработки зависит как от применяемого оборудования, режущего инструмента, условий обработки так и от режимов резания. Ведение процесса на оптимальных режимах (параметрическая оптимизация) является достаточно простым и действенным методом повышения эффективности процессов механической обработки и позволяет в зависимости от конкретных условий производства обеспечить повышение производительности обработки или снижение ее себестоимости на 15-30%.
Определение оптимальных режимов обработки заготовки на металлорежущих станках состоит в том, чтобы на основе знания свойств заготовки, режущего инструмента, физических законов их взаимодействия в процессе обработки, кинематических и динамических возможностей станка и свойств системы СПИД, назначать такие режимы, которые обеспечат формообразование детали в строгом соответствии с техническими условиями при наименьших затратах труда.
Задача расчета элементов оптимальных режимов резания является сложной технико-экономической задачей. Для ее успешного решения необходимо использовать теоретические положения учения о резании металлов, а также современные математические методы теории исследования операций и ЭВМ. Режимы резания (скорость резания - V, глубина резания - t, подача - s) должны отвечать как технологическим требованиям, так я вполне конкретным экономическим.
Технологический процесс механической обработки резанием характеризуется параметрами (величинами, определяющими значения элементов процесса) и показателями (различными константами, коэффициентами и т.п., определяющими различные количественные характеристики процесса). К параметрам относятся следующие величины: параметры заготовки, станка, инструмента, приспособления. Между параметрами существуют геометрические и кинематические связи. Показатели технологической операции подразделяются на
|
|
|
- технические, характеризующие состояние станка, инструмента, заготовки в процессе обработки, приспособления, отдельные звенья станка и др.;
- технологические, характеризующие деталь после обработки (точность размеров и геометрической формы, шероховатость и взаимное расположение поверхностей и др.);
- организационно-производственные, обусловленные заданной производительностью станка, тактом и др.;
- экономические, определяющие себестоимость обработки.
Функциональные связи между параметрами и показателями технологической операции являются техническими ограничениями режимов резания и в совокупности составляют математическую модель оптимальных режимов резания.
Наиболее важными ограничениями являются следующие: режущие возможности инструмента; мощность привода главного движения станка; шероховатость обработанной поверхности; прочность слабого звена механизма подачи станка; кинематические возможности станка по скорости главного движения и подачи; точность обработка; стойкость инструмента и др.
Кроме перечисленных, на выбор режимов резания влияют и другие ограничения: жесткость узлов станка, приспособления, вибрации при резании, нагрев детали и инструмента, сила закрепления заготовки и ряд других.
Цель оптимизации- определить возможность такого построения технологического процесса (ТП), при котором он обеспечивает максимальный эффект.
Оптимизация технологического процесса - это поиск такого варианта ТП из числа возможных в определённых условиях, который обеспечивает минимальные трудовые и материальные затраты при изготовлении продукции заданного качества.
Основные этапырешения задачи оптимизации:
|
|
|
1. Постановка задачи, анализ исходных данных.
2. Обоснование критерия оптимизации.
3. Выявление основных закономерностей и особенностей оптимизируемого ТП.
4. Построение математической модели ТП.
5. Разработка алгоритма и программы решения задачи оптимизации.
6. Анализ полученных результатов, принятие решения.
Постановка задачидолжна отражать конкретные условия и возможные варианты осуществления ТП, т.е. варианты используемого оборудования, диапазон возможных изменений режимов резания, возможные варианты базирования, последовательности выполнения технологических переходов и т.д. При этом должны быть приведены все необходимые данные для решения задачи.
Пример. Найти оптимальный режим сверления отверстия диаметром d = 20 мм в заготовке из стали 45 (твердость НВ = 2300 МПа, временное сопротивление разрыва sв = 600 МПа).
Станок 2А125: по паспортным данным станка частота вращения шпинделя может изменяться в пределах n = 97 ¸ 1360 об/мин; подача - в пределах S = 0,10 ¸ 0,81 мм/об.
Допустимая осевая нагрузка на шпиндель Pmax=9000 H.
Мощность двигателя N = 2,8 кВт.
Стойкость инструмента принимаем равной Т = 60 мин.
Обоснование критериев оптимизации. Наиболее универсальными критериями оптимизации ТП являются экономические критерии, т.к. они учитывают затраты как живого, так и овеществленного труда. В ряде случаев, когда экономические критерии зависят только от производительности изготовления изделий (при неизменном оборудовании, инструменте и прочих накладных расходах), оптимизацию ТП можно осуществлять по критерию обеспечения максимальной производительности обработки.
В условиях примера максимальная производительность П операции достигается при минимальном основном времени То:
 , (1)
, (1)
где l – длина рабочего хода инструмента, мм.
Выявление основных закономерностей ТП осуществляется на основе аналитических, экспериментальных исследований или на основе обобщения и анализа накопленного труда в промышленности.
Для условий примера из теории резания для сверлильных операций известны следующие зависимости:
Скорость резания
 , мм/мин; (2)
, мм/мин; (2)
осевая сила резания
 , Н (3)
, Н (3)
крутящий момент резания

 , Hм (4)
, Hм (4)
где Км – коэффициент материала заготовки;
|
|
|
См – коэффициент, учитывающий влияние прочих факторов.
Значения коэффициентов и показателей степеней в формулах (2)-(4) определяются по справочным данным.
Построение математической модели ТП осуществляется на основе использования установленных закономерностей ТП, путём ввода соответствующих ограничений и построения целевой функции.
Математическая модель ТП представляет собой совокупность системы неравенств, отражающих основные условия осуществления ТП и принятые ограничения, и подлежащей оптимизации целевой функции. С одной стороны этих выражений должны находиться искомые факторы ТП, а с другой - неизменные параметры процесса.
Например, построим математическую модель операции сверления.
Так как
 ,
,
приравниваем правые части этого выражения и равенства (2) и после преобразований получаем
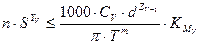 . (5)
. (5)
Знак неравенства в выражении (5) возникает от того, что стойкость инструмента Т обычно ограничена с одной стороны - снизу, но в принципе может быть и больше заданной величины.
Приравнивая выражение (3) допустимой станком осевой силе резания Рпах и учитывая, что фактическая сила может быть и меньше этой величины, получаем
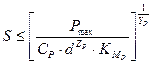 . (6)
. (6)
Аналогично с учетом ограничения по мощности резания
 .
.
Из выражения (4) получаем
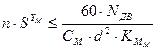 . (7)
. (7)
Известно выражение для расчета подачи, допустимой прочностью сверла
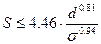 , мм/об. (8)
, мм/об. (8)
Кроме того, следует учесть допустимые конструкцией станка предельные значения частот вращения и подач:
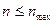 , (9)
, (9)
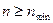 , (10)
, (10)
 , (11)
, (11)
 . (12)
. (12)
Прологарифмируем выражения (1), (5) – (12) и приведем их к единой системе:
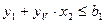 - условие обеспечения заданной стойкости; (13.1)
- условие обеспечения заданной стойкости; (13.1)
 - условие предотвращения поломок станка; (13.2)
- условие предотвращения поломок станка; (13.2)
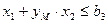 - ограничения по мощности двигателя; (13.3)
- ограничения по мощности двигателя; (13.3)
 - ограничения по прочности инструмента; (13.4)
- ограничения по прочности инструмента; (13.4)
 - ограничения максимальной частоты вращения
- ограничения максимальной частоты вращения
шпинделя n; (13.5)
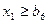 - ограничение минимальной частоты вращения
- ограничение минимальной частоты вращения
шпинделя n; (13.6)
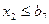 - ограничение максимальной величины подачи S; (13.7)
- ограничение максимальной величины подачи S; (13.7)
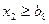 - ограничение минимальной величины подачи S; (13.8)
- ограничение минимальной величины подачи S; (13.8)
 - целевая функция, (13.9)
- целевая функция, (13.9)
где
 ,
,
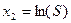 ,
,
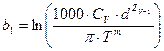 ,
,
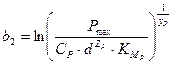 ,
,
 , (14)
, (14)
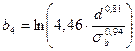 ,
,
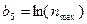 ,
,
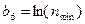 ,
,
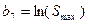 ,
,
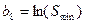 .
.
Выражение (13) представляет собой математическую модель технологического перехода сверления отверстия.
|
|
|
Разработка алгоритма и программы решения задачи оптимизации предусматривает:
1. Выбор метода решения задачи оптимизации.
2. Разработку алгоритма решения задачи и его описание.
В зависимости от задачи оптимизации и вида математической модели технологического процесса используют различные методы математического программирования. В данном случае наиболее приемлемыми являются методы решения задач линейного программирования, применяемые при линейных выражениях, описывающих математическую модель.
Линейным программированием называется раздел прикладной математики, изучающий теорию, приложение и методы решения конечных систем неравенств с конечным числом вещественных неизвестных.
Наиболее часто при решении задач линейного программирования применяется симплекс-метод. Алгоритм решения задачи оптимизации этим методом состоит в определении множества допустимых значений искомых параметров, из которых затем выбираются такие значения, которые обеспечивают min (max) критерия оптимизации.
Рассмотрим графическую интерпретацию симплекс-метода.
Для условий рассматриваемого примера в результате подстановки в неравенства (13) численных значений исходных параметров получилась следующая математическая модель исследуемого процесса:
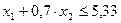 , (15.1)
, (15.1)
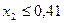 , (15.2)
, (15.2)
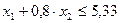 , (15.3)
, (15.3)
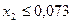 , (15.4)
, (15.4)
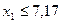 , (15.5)
, (15.5)
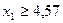 , (15.6)
, (15.6)
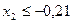 , (15.7)
, (15.7)
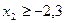 , (15.8)
, (15.8)
 . (15.9)
. (15.9)
Графически это выглядит так как изображено на рис. 2.9.
Анализ полученных результатов заключается в построении графических зависимостей, обеспечивающих наглядное представление решаемой задачи и определении оптимальных значений исходных факторов. На заданном графике заштрихована область допустимых значений х1 , х2. Чтобы выбрать оптимальное значение, надо провести линию x1 = fo - x2 под углом 45° и перемещать её до касания с многоугольником сверху, если требуется максимальное значение функции (для рассматриваемого случая) и снизу, если требуется минимальное значение функции fо.
Для рассматриваемого случая оптимальной точкой (точкой касания линии fо с многоугольником) является точка с координатами х2 = - 0,21; х1 = 5,47, откуда S = 0,81мм /об; n = 239 мм /об. По справочным данным: S = 0,38 ¸ 0,64 мм/об; n = 336 об/мин.
Таким образом, основное время сверления отверстия, длиной 10 мм, составляет:
- с использованием режима, установленного по справочным данным: Т = 10/(0,5×336) = 0,0595 мин;
- с использованием найденных режимов путём решения оптимизации задачи: Т =10/(0,81×239) = 0,0516 мин.

Рис. 2.9
Следовательно, решение оптимизации задачи обеспечивает повышение производительности обработки на 15%.
|
|
|
2.2.10. Технико-экономическое сравнение вариантов выполнения
|
|
|


