 |
Принцип угловой модуляции.
|
|
|
|
АМПЛИТУДНАЯ МОДУЛЯЦИЯ СЛОЖНЫМИ МОДУЛИРУЮЩИМИ СИГНАЛАМИ.
На практике однотональные АМ сигналы используются редко. Более реален случай, когда модулирующий НЧ сигнал имеет сложный спектральный состав.
Математической моделью такого сигнала может быть, например, сумма вида
.
Подставим значение этого сигнала в общее выражение для АМ колебания
.
Введем совокупность парциальных коэффициентов модуляции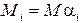 
и найдем спектр сигнала, так же, как и для однотонального АМ сигнала
Построим спектральные диаграммы модулирующего (рис.a) и промодулированного (рис.б) сигналов:
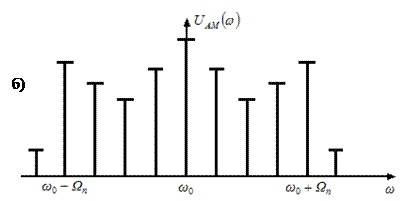
В спектре сложно-модулированного АМ сигнала, помимо несущего колебания, содержатся группы верхних и нижних боковых колебаний. Спектр верхних боковых колебаний является масштабной копией спектра модулирующего сигнала, сдвинутой в область высоких частот на величину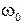 
. Спектр нижних боковых колебаний также повторяет спектральную диаграмму модулирующего сигнала, но располагается зеркально относительно несущей частоты .
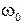Т.е. ширина спектра АМ сигнала равна удвоенному значению самой высокой частоты в спектре модулирующего НЧ сигнала.
Для более эффективного использования мощности АМ-сигнала применяют сигналы с подавленной несущей и такая модуляция называется балансной. В др. передатчиках (телевидение) используется передача информации с помощью одной боковой полосы частот. Она позволяет эффективно использовать мощность передатчика и сужает спектр рабочих частот. Такая модуляция называется однополосной.
СИГНАЛЫ С УГЛОВОЙ МОДУЛЯЦИЕЙ.
Как мы рассмотрели ранее, модуляция получается за счет того, что в несущем колебании 
изменяется один из параметров. Рассмотрим случаи, когда изменяется либо частота 
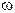, либо начальная фаза 
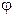. Т.к. величина 
называется полной фазой 
, которая определяет текущее значение фазового угла, то такие сигналы носят название сигналов с угловой модуляцией.
|
|
|
Принцип угловой модуляции.
Допустим, что полная фаза и передаваемое сообщение связаны соотношением
(32.1), где 
- несущая частота при отсутствии модуляции. Модуляцию, которая осуществляется по данному соотношению, называют фазовой модуляцией
(32.2).
На рисунке показаны осциллограммы модулирующего и промодулированного сигнала. При max S(t) фазовые сдвиги достигают max значения. Придельное значение фазового сдвига 
называют девиацией фазы, причем вследствие нелинейности модуляционной характеристики модулятора эти отклонения могут быть несимметричными и различают девиацию вверх 
и вниз 
.
На векторной диаграмме ФМ сигнал представлен как вектор постоянной длины, отклоняющийся от сдвига среднего положения на угол . Если же между частотой несущего колебания 
и модулирующим сигналом S(t) существует связь вида 
(32.3), то такая модуляция называется частотной.
Для полной фазы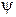 
и мгновенной частоты сигнала известно соотношение 
, тогда
. (32.4)
Поэтому частотно модулированный сигнал может быть записан в виде
(32.5).
В случае, если модуляция осуществляется гармоническим сигналом, то мгновенная частота будет изменяться по гармоническому закону 
. Величину Dw называют девиацией частоты сигнала. Используя (32.4) для полной фазы такого сигнала получим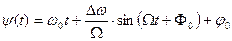 
. Величину 
, называют индексом однотональной частотной модуляции. Эта величина характеризует девиацию фазы сигнала. Если считать для простоты 
, то ЧМ сигнал будет иметь форму: 
(32.6).
Из (32.1) и (32.3) следует, что в первом случае фаза, а во втором – частота связаны линейно с модулирующим сигналом (с амплитудой), но не зависят от частоты модулирующего сигнала.
|
|
|
|
|
|
