 |
Объём сигнала, скорость передачи информации.
|
|
|
|
Рассмотрим случай, когда длительность передаваемого сигнала равна T, а высшая частота спектра равна FM. Строго говоря, такие условия несовместимы, т. к. сигнал конечной длительности обладает бесконечно широким спектром. Но практически всегда можно ограничиться рассмотрением полосы частот, за пределами которой энергия спектральных компонент пренебрежимо мала.
Пусть за время Т (рис. 9.3) передано N отсчётов, причём в соответствии с теоремой Котельникова расстояние между отсчётами выбиралось равным 
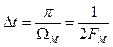, тогда: 
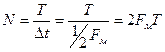, а ряд Котельникова будет иметь вид:
(9.11)
Рис.9.3
Число N – число степеней свободы сигнала f(t) или базы сигнала. Приняв это число за число переданных символов сигнала n по формуле 
можно вычислить количество информации, переданной за время T, но для этого еще необходимо оценить число возможных состояний m, которые можно различить в передаваемом сигнале. Это число зависит от уровня помех в канале связи. Если приращение сигнала меньше чем эффективное (среднеквадратичное) напряжение помехи 
, то такое приращение трудно зафиксировать. Поэтому величину , связанную с мощностью помехи соотношением = 
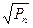принимают за единицу градаций сигнала в канале связи. Мощность сигнала при наличии передаваемого сообщения в канале равна Рс+Рп, а эффективное напряжение Uэ = 
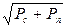. Тогда число возможных градаций сигнала будет равно 
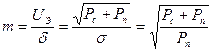(9.12)
Откуда количество информации (с учётом, что n>>1) равно
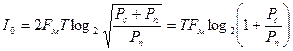(9.13)
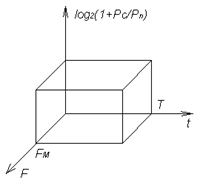Величину Iо иногда называют объёмом сигнала и изображают в виде параллелепипеда в трёхмерной системе координат (рис. 9.4). Если взять отношение 
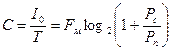(9.14)
получим скорость передачи информации. Очевидно, что для нормальной передачи информации пропускная способность канала связи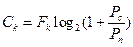 
должна быть не менее чем скорость поступающей информации, т.е. должно выполняться неравенство Ск≥С. При передаче буквенно-цифровой информации производится кодирование сигналов, т.е. представление их в виде комбинаций импульсов различной длительности. Различают равномерные и неравномерные коды. Большое распространение в устройствах связи получили равномерный код Бодо и неравномерный код Морзе.
|
|
|
ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ РЯДОМ КОТЕЛЬНИКОВА И ОШИБКИ АППРОКСИМАЦИИ.
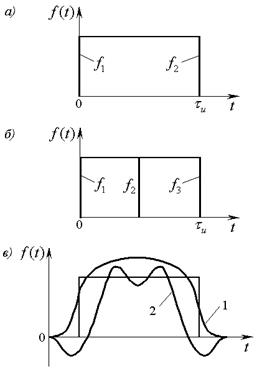Если известно, что большая часть энергии сигнала с неограниченным спектром сосредоточена в пределах ограниченной полосы частот, то с определенной погрешностью возможно представление таких сигналов с помощью ограниченного ряда Котельникова. Например, на рисунке показано представление прямоугольного импульса с помощью двух и трех отсчетов. В первом случае учитываются сигналы до частоты 
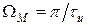. Во втором случае до частоты 
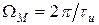. Соответствующие модели такого представления имеют вид:
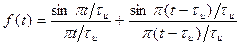. (1)
А во вором случае три отсчета:
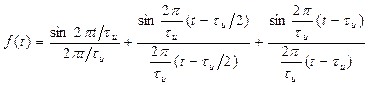. (2)
По формуле (1) построен график 1 на рисунке в и по формуле (2) – график 2.
С ростом числа отсчетов повышается точность аппроксимации сигнала рядом Котельникова.
Произвольный сигнал с неограниченным спектром при представлении его рядом Котельникова будет отличаться от сигнала с неограниченным спектром на величину ошибки. Поэтому, можно записать, что исходный сигнал
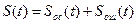, (3)
где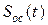 
– сигнал с ограниченным спектром, 
– сигнал ошибки.
Спектры этих сигналов не перекрываются, поэтому сигналы 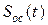и ортогональны. А их энергии, то есть квадраты норм, складываются: 
.
За абсолютную меру ошибки аппроксимации принимается расстояние, равное норме сигнала ошибки. Используя соотношения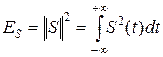 
, 
, 
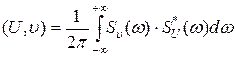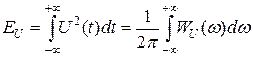можно, при известном энергетическом спектре 
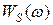, по теореме Рейли получить:
. (4)
УЗКОПОЛОСНЫЙ СИГНАЛ: ПРЕДСТАВЛЕНИЕ В КОМПЛЕКСНОЙ ФОРМЕ.
|
|
|
СПЕКТР СИГНАЛА.
Узкополосным называют сигнал, спектральная плотность которого сосредоточена в ограниченной полосе частот 
вблизи окрестности некоторой опорной частоты, причем выполняется условие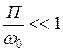 
. Математически такой сигнал может представляться разными моделями, например, 
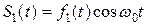или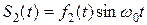 
.
Или в общем случае для представления узкополосного сигнала используют линейную комбинацию:
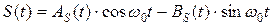. (1)
Функцию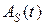 
называют синфазной амплитудой, а функцию 
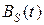– квадратурной амплитудой. Обе эти функции представляют собой НЧ (по сравнению с 
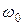) сигнал. Узкополосные сигналы могут представляться и в комплексной форме:
. (2)
Величину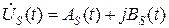 
(3) называют комплексной огибающей узкополосного сигнала. Не трудно показать, что вещественное представление (1) узкополосного сигнала связано с комплексным представлением соотношением:
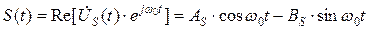. (4)
С физической точки зрения узкополосный сигнал можно рассматривать как квазигармоническое колебание, к которому для расчетов применим метод комплексных амплитуд. Комплексная огибающая узкополосного сигнала играет ту же роль, что и амплитуда простого гармонического колебания. Однако вектор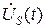 
в общем случае будет совершать колебания на комплексной плоскости, изменяясь по амплитуде и угловому положению.
Обозначим спектральную плотность комплексной огибающей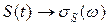 
. Тогда спектр узкополосного сигнала буде равен:
.
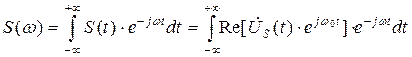Так как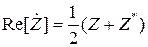 
, то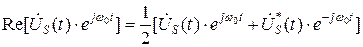 
. Тогда:
.
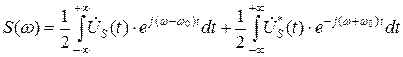То есть,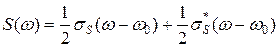 
. (5)
Таким образом, спектральная плотность узкополосного сигнала может быть найдена путем простого переноса спектра комплексной огибающей из окрестности нулевой частоты в окрестность точек с частотами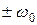 
. Амплитудный спектр компонент вдвое меньше, чем у спектра огибающей, и спектр в области отрицательных частот получается комплексно сопряженным. Ценность полученного соотношения состоит в том, что спектр узкополосного сигнала (в частности модулированного сигнала) можно найти по спектру огибающей модулирующего сигнала.
|
|
|
