Распознование сигналов в РТС. Помехоустойчивость сигналов в ситемах связи.

Распознавание сигналов в РТС. Используя свойства ортогональности функции по заданному сигналу можно определить вектор сигнала , вычислив . Действительно:

. (1)

Производя эти вычисления для всех функций 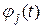можно получить все состояния вектора .

Для осуществления передачи и приема информации колебания 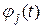в передатчике и приемнике должны вырабатываться синхронно, так как координаты однозначно задают сигнал и элемент , то вычисление этих координат равносильно определению переданного элемента . Рассмотренный результаты справедливы, когда линия связи не искажает форму сигнала и помехи в линии связи отсутствуют. В таком случае входной и выходной сигналы отличаются только масштабом.

, (2)

, а координаты в точке приема отличаются от переданных входных, но конфигурация векторов сигнала не изменяется и возможно осуществить их безошибочное распознавание.

Если линия связи не искажает сигнал, но имеет место помеха, то в точке приема имеем сигнал:

, (3)

где 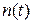– реализация помехи: аддитивные (они складываются к сигналу), мультипликативные (умножаются на сигнал и искажают его).

При восстановлении сигнала в приемнике, получим (при ):

, (4)

где – приращение, вызванное шумом – ошибка определения компоненты 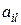вектора .

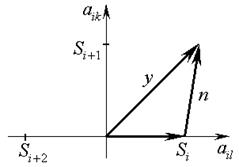Геометрически эта ситуация показана на рисунке, где принимаемый сигнал образован как геометрическая сумма переданного вектора и вектора помехи : .

Из рассмотренного следует, что при наличии помех необходимо разработать процедуру распознавания сигналов, то есть процедуру соотношения вектора с одним из векторов , которая обеспечила бы минимальное значение ошибок распознавания. Отсюда же следует, что набор из m векторов должен обеспечивать достижение минимума ошибок.

Последнее условие может быть выполнено, если выбрать векторы с максимально разнесенными концами, что достигается соответствующим размещением векторов в пространстве сигналов и увеличением энергии сигнала. Последнее всегда не желательно.

Наборы помехоустойчивых сигналов в системах связи (СС).

Таковыми для СС являются наборы сигналов, синтезированных в соответствии с формулами и обладающих геометрической конфигурацией, обеспечивающей максимальное разнесение концов векторов сигнала.

В зависимости от числа ортонормированных функций N, участвующих в формировании M сигналов. Наиболее часто используютсяследующие конфигурации векторов сигналов:

1) Бинарные противоположные сигналы: , , 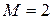, . Векторы сигналов выбираются так: , . Сигналы в этом случае могут быть выбраны в следующем виде:

, (5)

причем обычно гармоническое колебание.

2) Бинарные ортогональные сигналы: , , 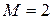, . Векторы и равны:

. (6)

В качестве ортонормированных функций можно выбрать колебания, рассмотренные в примере:

. (7)

Геометрически векторы и для бинарных противоположных сигналов представлены на рисунке а, а для бинарных ортогональных – на рисунке б. Внешние диаграммы будут зависеть от вида выбранных функций .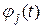

Бинарные противоположные сигналы должны обеспечивать большую помехоустойчивость, поскольку концы их векторов разнесены дальше, однако на практике использование ортогональных сигналов иногда оказывается проще. В практике радиосвязи кроме рассмотренных применяется большое число других помехоустойчивых сигналов, различающихся числом ортогональных функций 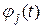, числом векторов , выбранными видами колебаний и другими показателями. Однако принцип использования ортонормированных функций и максимального разнесения концов векторов сохраняется.