 |
Способы упорядочения функции Уолша.
|
|
|
|
Функции Уолша являются естественным расширением функций Радемахера. Они получены Уолшем в 1923 г. и представляют полную систему ортонормированных прямоугольных функций.
Множество функций Уолша, упорядоченных по частости (по Уолшу), обычно обозначают следующим образом:
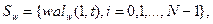(1)
где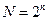 
, 
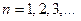. Нижний индекс 
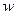показывает, что упорядочение осуществляется по Уолшу (по частости). Индекс 
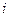соответствует 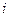-му элементу множества 
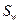. Обозначим через 
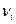частость функции 
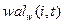. Для определения частости воспользуемся соотношением
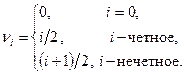(2)
Функции Уолша, упорядоченные по частости, аналогично тригонометрическим функциям можно подразделить на четные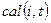 
и нечетные 
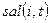, тогда
(3)
На рис.1 показаны первые восемь функций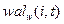 
. Частость каждой последующей функции Уолша больше или равняется частости предыдущей функции Уолша и имеет на одно пересечение нулевого уровня больше в открытом интервале 
.
Отсюда и следует название «упорядочение по частости». Дискретизация функций Уолша, (рис.1, а) в восьми равноотстоящих точках приводит к матрице (8x8), показанной на рис.1, б. Эту матрицу обозначают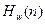 
,где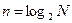 
и матрица будет иметь размер 
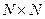, где строки — поляр функции Уолша, а столбцы - значения функции при 
, 
.
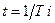а) 
б)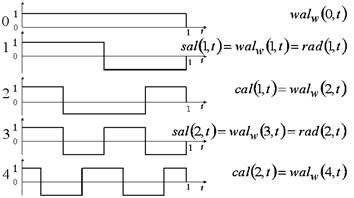 
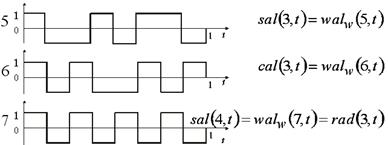
В матрице номера строк соответствуют номерам функций Уолша, номера столбцов — номерам отсчетов, значения элементов матрицы — значениям функций Уолша.
Функции Уолша при упорядочении по частости в общем случае можно получить из функций Радемахера 
по формуле
, (4)
где 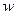– номер функции Уолша; 
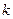– номер функции Радемахера; 
– показатель степени функции Радемахера, который принимает значение 0 или 1 в результате суммирования по модулю два, т.е. по правилу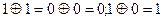 
разрядов двоичного числа 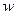. Например, для шестой функции Уолша (
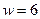), входящей в систему размером 
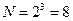, произведение (4) состоит из трех сомножителей вида:
|
|
|
при 
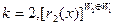, при 
, при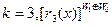 
.
Число в двоичной системе записывается совокупностью нулей и единиц. В нашем случае значения 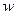и его разрядов показаны в таблице 1.
Таблица 1
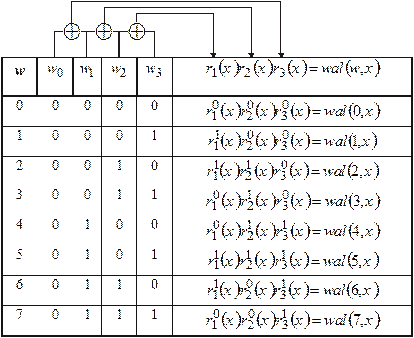
В таблице 1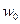 
- старший разряд числа, 
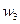- младший разряд числа .
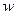Показатели степени функций Радемахера получаются равными:
.
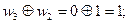
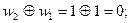
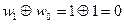Следовательно,
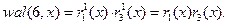
Правило получения показателей степеней для функций Радемахера схематически показано в табл.1, где стрелками указаны суммируемые разряды числа 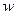и функции Радемахера, к которым относится полученный показатель степени.
Из рис. 1 видно, что четные номера функций Уолша относятся к четным функциям, а нечетные – нечетным функциям.
Другим способом упорядочения функций Уолша является способ упорядочения по Пэли, при котором аналитическая запись функций Уолша имеет вид
, (5)
где 
- двоичный номер функции, имеющий представление в двоичной форме:
, (6)
где 
- младший разряд двоичного числа, 
- старший разряд двоичного числа. При упорядочении по Пэли формирования функций Уолша необходимо взять произведение возведенных в степень функций Радемахера, номера которых совпадают с номерами соответствующих разрядов двоичного представления числа , а показатель степени каждой функции равен содержимому соответствующего разряда, т.е. 0 или 1. Причем младшей функции Радемахера соответствует младший разряд двоичной комбинации числа . В соответствии с этим правилом в табл. 2 приведены значения функций Уолша, упорядоченных по Пэли.
Таблица 2
| 
| 
| 
| 
| 
|
| 
| ||||
| 
| ||||
| 
| ||||
|
| ||||
| 
| ||||
| 
| ||||
| 
| ||||
| 
|
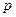
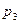
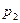
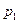
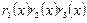
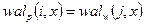
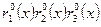
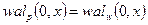
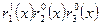
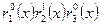
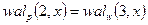
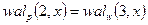
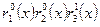
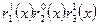
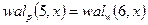
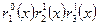
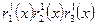
Функции Радемахера в таблице 2 показаны в форме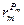 
.
Сравнение произведений и степеней функций Радемахера, записанных в таблицах 1 и 2, показывает, что между функциями Уолша, упорядоченными по Пэли и по Уолшу, существует соответствие, которое отражено в последнем столбце табл.2. В соответствии с функциями Уолша, упорядоченными по Пэли, также может быть построена матрица отсчетов, аналогичная показанной на рис.1,б.
|
|
|
Следующим распространенным способом упорядочения является упорядочение по Адамару. Функции Адамара 
формируют с помощью матриц Адамара.
Матрицей Адамара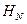 
порядка 
называется квадратная матрица размером 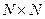и с элементами 
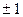, обладающая свойством
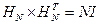, (7)
где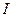 
- единичная матрица; 
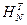- транспонированная матрица. Матрицы Адамара можно строить, используя рекуррентное соотношение:
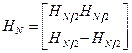. (8)
Например, начиная с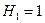 
, находим:
; 
;
.
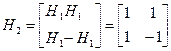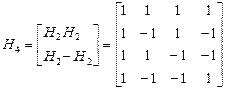Сравнивая полученную матрицу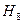 
с матрицей отсчетов для функций Уолша, упорядоченных по Уолшу (см. рис.1, б), видим, что между первыми восемью функциями, упорядоченными по Уолшу и Адамару, существует следующее соответствие:
|
|
|
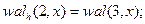
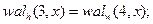
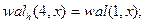
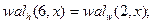
