Дифференцирование вектор-функции

Е.Г. Романова

Дифференциальная геометрия

Краткий конспект лекций

Конспект лекций содержит основные понятия дифференциальной геометрии, сведения из теории кривых и поверхностей.

Конспект лекций предназначен для студентов специальности 010503

“Математическое обеспечение и администрирование информационных систем” Пензенского государственного университета.

 

 

 

 

Содержание

Содержание. 2

1. Векторная функция скалярного аргумента. 4

1.1 Определение вектор-функции. Предел. Непрерывность. 4

1.2. Дифференцирование вектор-функции. 5

1.3. Интеграл от векторной функции по скалярному аргументу. 7

2. Сведения из теории кривых. 7

2.1. Элементарная кривая. 7

2.2. Касательная прямая к кривой. 9

2.3. Соприкасающаяся плоскость кривой. 10

2.4. Длина дуги как параметр. 11

2.5. Кривизна кривой. 13

2.6. Кручение кривой. 16

2.7. Формулы Френе. 18

3. Теория поверхностей в дифференциальной геометрии. 23

3.1. Элементарная поверхность. 23

3.2. Регулярная поверхность. 25

3.3. Кривые на поверхности. 26

3.4. Касательная плоскость и нормаль к поверхности. 26

3.5. Измерение на поверхности длин, углов, площадей. Первая квадратичная форма поверхности. 28

3.6. Площадь поверхности. 30

3.7. Вторая квадратичная форма поверхности. 31

3.8. Кривизна кривой, лежащей на поверхности. 33

3.9. Главные направления и кривизны поверхности. 34

3.10. Внутренняя геометрия поверхности. 35

Литература. 37

Дифференциальная геометрия – это часть математики, которая изучает геометрические образы, в первую очередь кривые и поверхности, применяя методы математического анализа.

 

Векторная функция скалярного аргумента

 

Определение вектор-функции. Предел. Непрерывность

Кри­вые и поверхности удобно задавать функциями, принимающими векторные значения или вектор-функциями. Кратко сформулируем основные понятия анализа применительно к вектор-функциям.

Пусть – трёхмерное евклидово пространство и I – некоторый числовой промежуток.

Определение 1.1. Если каждому числу 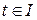по некоторому закону поставлен в соответствие определённый вектор из пространства , что в промежутке I задана векторная функция скалярного аргумента или вектор–функция .

Здесь – некоторые непрерывные скалярные функции.

С вектор-функцией связыва­ются следующие наглядные представ­ления. Если от­кладывать от начала координат векторы , отвечающие различным значениям аргумента t, то концы этих векторов составят некоторую кривую – график вектор-функции , обычно называемую годографом функции (рис. 1 ). Если рассматривать аргумент t как время, то годограф функции – это траектория движения некоторой точки.

Дифференцирование вектор-функции

Вектор-функция непрерывна в точке t₀ тогда и только тогда, когда все три ее компоненты – скалярные функции – непрерывны в точке t ₀. Сумма, разность, ска­лярное и векторное произведения непрерывных вектор-функций непрерывны.

Определение 1.2. Векторная функция имеет в точке t производную, если существует предел отношения 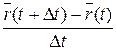при .

Обозначается производная через или . Таким образом, . (1.1)

Легко проверить, что суще­ствование равносильно существованию трех производных х ' ( t), у ' (t)и z ' (t), причем .

Определение 1.3. Векторная функция называется дифференцируемой на множестве или простой дифференцируемой, если она дифференцируема в каждой точке этого множества.

Вектор направлен по секущей ММ ₁ годографа функции (рис. 2), а направление вектора – это направление предельнойпрямой, к которой стремится эта секущая, когда точка М ₁ прибли­жается к М, т. е. направление касательной к годографу в точке М.

Для вектор-функции имеют место следующие правила дифферен­цирования:

1) если , то ;

2) где ;

3) , где u (t) – скалярная функция;

4) ;

5) 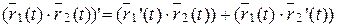– для скалярного произведения;

6) – для векторного произведения;

7) если и , то – правило дифференцирования сложной функции.

 

Пример 1.1. Задана векторная функция где a, b – const. Найти .

Решение. Координатами вектора является числовые функции

x (t) = a cos t, y (t) = a sin t, z (t) = bt.

Тогда ■

Отметим следующие частные случаи дифференцирования вектор-функции:

а) Производная вектора постоянного направления. Пусть вектор имеет постоянное направление (т. е. от t зависит лишь его длина). Тогда векторы и коллинеарны. Дей­ствительно, в этом случае мож­но записать в виде , где и(t) – скаляр, а – постоянный вектор, например единичный. Тогда , т.е. .

б) Производная вектора постоянной длины. Если | | = const, то векторы и взаимно ортогональны. Действительно, в этом случае (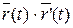) = const; дифференцируя это равенство, получаем , т.е. 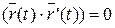, что и требовалось доказать.

Определение 1.4. Дифференциалом вектор-функции называется вектор .

Иначе говоря, .

Дифференциал вектор-функции равен произведению ее произ­водной на дифференциал (т. е. приращение) независимой переменной. Как и в случае скалярной функции, дифференциал d 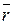вектор-функции отличается от ее приращения ∆ 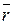на величину выше первого порядка малости относительно ∆ t.

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: