 |
Касательная прямая к кривой
|
|
|
|
Пусть задана гладкая кривая 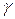 , и её уравнение имеет вид
, и её уравнение имеет вид  или
или
 .
.
Возьмём на линии 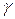 две точки М и М 1, соответствующие значениям параметра t и
две точки М и М 1, соответствующие значениям параметра t и  (рис. 2). Вектор
(рис. 2). Вектор 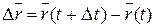 является направляющим вектором секущей прямой ММ 1. Следовательно, вектор
является направляющим вектором секущей прямой ММ 1. Следовательно, вектор  также направляющий вектор секущей ММ 1. Когда
также направляющий вектор секущей ММ 1. Когда  , точка М 1 неограниченно приближается по кривой к точке М, вектор
, точка М 1 неограниченно приближается по кривой к точке М, вектор  стремится занять положение касательной в точке М (касательная к кривой в точке определяется как предельное положение секущей).
стремится занять положение касательной в точке М (касательная к кривой в точке определяется как предельное положение секущей).
Вместе с тем отношение  стремится к производной
стремится к производной  как к своему пределу. Отсюда следует, что производная от радиус – вектора точки параметрической кривой есть вектор, направленный по касательной к этой кривой в сторону возрастания параметра t.
как к своему пределу. Отсюда следует, что производная от радиус – вектора точки параметрической кривой есть вектор, направленный по касательной к этой кривой в сторону возрастания параметра t.
Чтобы получить уравнение касательной к вектор – функции, выразим радиус – вектор  любой точки касательной прямой через радиус – вектор
любой точки касательной прямой через радиус – вектор 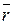 начальной точки, направляющий вектор
начальной точки, направляющий вектор  и параметр
и параметр  .
.
Тогда  – уравнение касательной в параметрическом виде.
– уравнение касательной в параметрическом виде.
Заменяя это векторное уравнение скалярными функциями, получим параметрические уравнения касательной:

или, исключив параметр  , каноническое уравнение касательной:
, каноническое уравнение касательной:
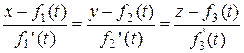 .
.
Указанный способ определения касательной, очевидно, неприменим к той точке  , для которой
, для которой  . Такие точки будем называть особыми точками кривой и будем исключать их из рассмотрения.
. Такие точки будем называть особыми точками кривой и будем исключать их из рассмотрения.

Соприкасающаяся плоскость кривой
 Пусть PQ — касательная в точке Р к кривой γ (рис. 3). Через касательную PQ и точку M кривой проведем плоскость PQM. Плоскость π, к которой стремится плоскость PQM при М → Р, называется соприкасающейся плоскостью к кривой γ в точке Р.
Пусть PQ — касательная в точке Р к кривой γ (рис. 3). Через касательную PQ и точку M кривой проведем плоскость PQM. Плоскость π, к которой стремится плоскость PQM при М → Р, называется соприкасающейся плоскостью к кривой γ в точке Р.
Справедливо следующее утверждение.
Утверждение 2. 1. Регулярная, дважды дифференцируемая кривая γ без особых точек имеет соприкасающуюся плоскость p каждой точке, в которой векторы  и не коллинеарны.
и не коллинеарны.
|
|
|
Получим уравнение соприкасающейся плоскости в другой форме. Так как векторы  –
–  ,
,  ,
,  компланарны, то вектор
компланарны, то вектор  удовлетворяет следующему уравнению
удовлетворяет следующему уравнению
|
 .
.
Если X, У, Z — координаты вектора  (координаты переменной точки s плоскости π), а х (t), у (t), z (t)— координаты вектора
(координаты переменной точки s плоскости π), а х (t), у (t), z (t)— координаты вектора  , то в координатной форме уравнение (2.1) запишется следующим образом:
, то в координатной форме уравнение (2.1) запишется следующим образом:
|
 .
.
Уравнение (2.2), очевидно, представляет собой уравнение соприкасающейся плоскости.
Замечание 2.1. Соприкасающаяся плоскость определена геометрически с помощью предельного перехода, и поэтому в случае ее существования она будет единственна. Отсюда и из доказанного в этом пункте утверждения вытекает, что если в данной точке кривой существует соприкасающаяся плоскость, то при любой параметризации кривой вектор  параллелен этой плоскости.
параллелен этой плоскости.
Длина дуги как параметр
Выберем на гладкой кривой  :
:  некоторую точку
некоторую точку  ,соответствующую значению параметра
,соответствующую значению параметра 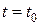 и назовём её начальной точкой.
и назовём её начальной точкой.
Длина дуги, имеющий начало в точке  и конец в произвольной точке М, определяется, как известно из курса математического анализа, по формуле:
и конец в произвольной точке М, определяется, как известно из курса математического анализа, по формуле:

или в векторной форме  .
.
Следовательно, длина дуги s = s (t) является дифференцируемой функцией параметра t.
Так как производная этой функции  во всех точках кривой, то функция s = s (t) является возрастающей функцией параметра t. Ввиду того, что все точки t кривой
во всех точках кривой, то функция s = s (t) является возрастающей функцией параметра t. Ввиду того, что все точки t кривой 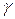 и значения длины дуги s находятся во взаимно однозначном и непрерывном соответствии, s можно принять за новый параметр. Такая параметризация называется естественной или натуральной параметризацией, где s – естественный или натуральный параметр. Так как
и значения длины дуги s находятся во взаимно однозначном и непрерывном соответствии, s можно принять за новый параметр. Такая параметризация называется естественной или натуральной параметризацией, где s – естественный или натуральный параметр. Так как  , то
, то  и
и  .
.
Отсюда следует, что  – единичный вектор. Будем называть его единичным вектором касательной к линии в точке M и обозначать через
– единичный вектор. Будем называть его единичным вектором касательной к линии в точке M и обозначать через  , т.е.
, т.е.  или
или  . Тогда
. Тогда  .
.
|
|
|
Задача 2.1. Найти длину дуги гиперболической винтовой линий  заключённую между точками O и t. Параметризовать припомощи естественного параметра.
заключённую между точками O и t. Параметризовать припомощи естественного параметра.
Решение. Найдём длину дуги  . Вычислим отдельно
. Вычислим отдельно 
Тогда 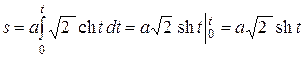 . Выразим из равенства
. Выразим из равенства  параметр t. Имеем
параметр t. Имеем  и, следовательно,
и, следовательно,  .
.
Таким образом, получены естественные уравнения кривой
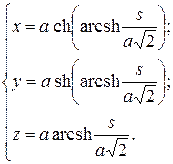

Кривизна кривой
 Пусть Р — произвольная фиксированная точка регулярной кривой γ без особых точек и M — точка этой кривой, отличная от Р. Обозначим через φ угол между касательными в точках Р и М, а через s — длину дуги РМ (рис. 4).
Пусть Р — произвольная фиксированная точка регулярной кривой γ без особых точек и M — точка этой кривой, отличная от Р. Обозначим через φ угол между касательными в точках Р и М, а через s — длину дуги РМ (рис. 4).
 Определение 2.7. Кривизной k кривой γ в точке Р называется предел отношения φ / l при s→ 0т. е. при М→P или
Определение 2.7. Кривизной k кривой γ в точке Р называется предел отношения φ / l при s→ 0т. е. при М→P или 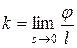 .
.
Справедливо следующее утверждение.
Утверждение 2.2. Регулярная (дважды дифференцируемая) кривая γ без особых точек имеет в каждой точке определенную кривизну k.
Докажем это утверждение.
Пусть точки Р и М кривой отвечают соответственно значениям t и t+ ∆ t параметра. Вычислим sin φ и s. Так как кривая γ регулярна, то  ≠ 0 в любой точке кривой γ, и поэтому
≠ 0 в любой точке кривой γ, и поэтому
|
 ,
,
|
 ,
,
где  →0 при ∆ t→ 0.
→0 при ∆ t→ 0.
Отметим, что при преобразованиях выражения для s мы воспользовались формулой среднего значения для интеграла и непрерывностью функции  .
.
Преобразуем выражение (2.3) для sin φ. По формуле Тейлора
 , α →0 при t →0.
, α →0 при t →0.
С помощью этой формулы выражение (2.3) для sin φ принимает следующий вид:
|

где β →0 и ε→ 0 при ∆ t → 0.
Обращаясь к формулам (2.4) и (2.5) и используя при φ ≠0 тождество
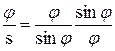 (при φ = 0 отношение
(при φ = 0 отношение  равно нулю), получим
равно нулю), получим
|
 ,
,
где β и μ стремятся к нулю при ∆ t→ 0. Так как φ → 0 при ∆ t →0, то  при ∆ t → 0. Поэтому из соотношения (2.6) следует, что при ∆ t →0, т.е. M→P предел
при ∆ t → 0. Поэтому из соотношения (2.6) следует, что при ∆ t →0, т.е. M→P предел  существует и равен
существует и равен  . Утверждение доказано. ■
. Утверждение доказано. ■
Итак, при условиях утверждения кривизна k существует и может быть найдена по формуле
|
 .
.
|
 , то
, то 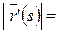 1 и вектор
1 и вектор  ортогонален вектору
ортогонален вектору  . В этом случае, очевидно, формула (2.7) примет следующий вид
. В этом случае, очевидно, формула (2.7) примет следующий вид
 .
.
На всей линии  кривизна k есть функция параметра s, т. е. k=k (s). Если в данной точке M имеем
кривизна k есть функция параметра s, т. е. k=k (s). Если в данной точке M имеем  , то число
, то число  называется радиусом кривизны линии в точке M.
называется радиусом кривизны линии в точке M.
|
|
|
Таким образом, если линия задана в естественной параметризации, то её кривизна вычисляется по формуле:

или в координатах:
 .
.
Примем без доказательства следующее утверждение.
Утверждение 2.3. Для того, чтобы линия была простейшей (прямая, отрезок, луч) необходимо и достаточно, чтобы кривизна была равна нулю в каждой точке этой линии.
Кручение кривой
Пусть Р — произвольная фиксированная точка регулярной кривой  без особых точек и М — точка этой кривой, отличная от Р. Обозначим через φ угол между соприкасающимися плоскостями в точках Р и М, а через s – длину дуги РМ.
без особых точек и М — точка этой кривой, отличная от Р. Обозначим через φ угол между соприкасающимися плоскостями в точках Р и М, а через s – длину дуги РМ.
Определение 2.8. Абсолютным кручением |χ| кривой γ в точке Р называется предел отношения φ/s при s → 0(т. е. при М→Р).
Справедливо следующее утверждение.
Утверждение 2.4. Регулярная (трижды дифференцируемая) кривая γ без особых точек имеет в каждой точке, где кривизна отлична от нуля, определенное абсолютное кручение.
Докажем это утверждение.
|
 и
и  . По формуле Тейлора с учетом равенства
. По формуле Тейлора с учетом равенства  получим
получим

где α → 0 при ∆ t → 0.
Для вычисления предела φ/s при s →0 нам понадобится значение синуса угла φ между нормалями к соприкасающимся плоскостям в точках Р и М. Для этой цели найдем модуль векторного произведения  и
и  , а также произведение модулей этих векторов. С помощью (2.9) получим
, а также произведение модулей этих векторов. С помощью (2.9) получим
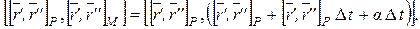
Отсюда, используя распределительное свойство векторного произведения и известную формулу  для двойного векторного произведения, найдем
для двойного векторного произведения, найдем


где  , и поэтому β →0 при ∆ t→ 0. Из последнего выражения для
, и поэтому β →0 при ∆ t→ 0. Из последнего выражения для  получаем следующую формулу:
получаем следующую формулу:
|

где ε →0 при ∆ t→ 0.
Путем аналогичных рассуждений получается также следующая формула:
|
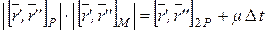
где μ →0 при ∆ t→ 0.
Из формул (2.10) и (2.11) получаем нужное нам выражение для sin φ:
 .
.
Отметим, что в этом выражении значения производных векторной функции  вычислены в точке Р.
вычислены в точке Р.
|
|
|
|
 .
.
Обращаясь к выражению (2.12) для s, используя только что полученную формулу для sin φ иизвестный предел  при φ → 0, убедились, что предел
при φ → 0, убедились, что предел  при s → 0 существует и равен
при s → 0 существует и равен  .
.
Итак, в условиях утверждения абсолютное кручение | χ| существует и может быть найдено по формуле
| (12.22) |
 .
.
Определим кручение χ кривой с помощью равенства
| (12.23) |
|
 .
.
Формулы Френе
Рассмотрим регулярную (трижды непрерывно дифференцируемую) кривую  . Если в
. Если в  выбрана прямоугольная система координат, то
выбрана прямоугольная система координат, то  .
.
Вектор  является единичным вектором касательной к линии
является единичным вектором касательной к линии  в точке M, где
в точке M, где  .
.
Вектор  называется вектором кривизны линии
называется вектором кривизны линии  в точке M и
в точке M и  .
.
Прямая, проходящая через точку M в направлении  называется главной нормалью линии
называется главной нормалью линии  в точке M (рис. 5).
в точке M (рис. 5).

Имеем 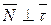 , так как вектор
, так как вектор  – вектор постоянной длины и, следовательно, перпендикулярен вектору
– вектор постоянной длины и, следовательно, перпендикулярен вектору  . Отсюда, главная нормаль перпендикулярна касательной.
. Отсюда, главная нормаль перпендикулярна касательной.
Вектор  называется единичным вектором главной нормали, т.е.
называется единичным вектором главной нормали, т.е.  =1. Так как
=1. Так как  , то
, то  и, следовательно,
и, следовательно,  или
или
 . (2.14)
. (2.14)
Определим ещё вектор 
Прямая, проходящая через точку M в направлении вектора  называется бинормалью линии
называется бинормалью линии  в точке M, а вектор
в точке M, а вектор  – единичный вектор бинормали. Имеем,
– единичный вектор бинормали. Имеем, 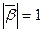 .
.
Плоскость, содержащая векторы  и
и  является соприкасающейся плоскостью; содержащая векторы
является соприкасающейся плоскостью; содержащая векторы  и
и  – нормальной плоскостью; содержащая векторы
– нормальной плоскостью; содержащая векторы  и
и  – спрямляющей плоскостью.
– спрямляющей плоскостью.
Трёхгранник с вершиной в точке M, образованный этими тремя плоскостями, называются сопровождающим трёхгранником пространственной кривой (рис. 5).
Так как вектор  – единичный, т.е. постоянной длины, то
– единичный, т.е. постоянной длины, то  и значит вектор
и значит вектор  , параллелен спрямляющейся плоскости. Поэтому его можно разложить по векторам
, параллелен спрямляющейся плоскости. Поэтому его можно разложить по векторам  и
и 
 , (2.15)
, (2.15)
где  – координаты в базисе
– координаты в базисе 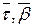 .
.
Тождество  дифференцируем по параметру s:
дифференцируем по параметру s:  . Если в этом равенстве
. Если в этом равенстве  и
и  заменить формулами (2.14) и (2.15), то получим
заменить формулами (2.14) и (2.15), то получим  или
или  . Учитывая, что
. Учитывая, что  , т.к. это скалярное произведение единичных векторов, а
, т.к. это скалярное произведение единичных векторов, а  , как скалярное произведение перпендикулярных векторов. Тогда будем иметь, что
, как скалярное произведение перпендикулярных векторов. Тогда будем иметь, что  и, отсюда,
и, отсюда,  . Формула (2.15) принимает вид после подстановки
. Формула (2.15) принимает вид после подстановки 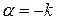
 . (2.16)
. (2.16)
Тождество  дифференцируем по параметру s:
дифференцируем по параметру s:
 .
.
Заменяя здесь векторы  и
и  их выражения через (2.12) и (2.14), находим, что
их выражения через (2.12) и (2.14), находим, что
 .
.
Отсюда  или
или  . Здесь взят знак “минус“, так как тройка векторов
. Здесь взят знак “минус“, так как тройка векторов  – левая; а число
– левая; а число  есть кручение линии
есть кручение линии 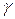 в точке M.
в точке M.
|
 ,
,  ,
,  .
.
Вся теория гладких линии основана на применении этих формул.
Найдём формулу для вычисления кручения, если линия 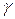 задана естественным уравнением
задана естественным уравнением  или
или  .
.
Первую формулу Френе можно записать так:  . Продифференцируем это соотношение по s и используем вторую формулу Френе:
. Продифференцируем это соотношение по s и используем вторую формулу Френе:  , получим
, получим
|
|
|
 .
.
Таким образом, смешанное произведение векторов по базису  найдётся, как
найдётся, как
 .
.
Отсюда получаем искомую формулу для кручения линии:
|

или в координатах 
|
 .
.
Линия  называется плоской, если все её точки лежат в некоторой плоскости.
называется плоской, если все её точки лежат в некоторой плоскости.
Примем без доказательства следующее утверждение.
Теорема 2.1. Кручение плоской линии во всех точках равно нулю.
Верно и обратное утверждение.
Пример 2.2. Найти кривизну и кручение винтовой линии  , a >0.
, a >0.
Решение. Найдем производные вектор – функции
 ,
, 
 ,
,
 .
. 

Теперь определим векторное произведение

Далее для смешанного произведения имеем
 .
.
Найдём длины векторов.
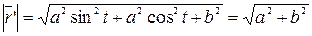 ,
,
 ,
,
 .
.
Отсюда кривизнабудет равна  , кручение
, кручение  .
.
Следовательно, для винтовой линии кривизна и кручение постоянны. ■
|
|
|


