Теория поверхностей в дифференциальной геометрии

Элементарная поверхность

Определение 3. 1. Область на плоскости называется элементарной областью, если она является образом открытого круга при гомеоморфизме, т.е. при взаимно однозначном и непрерывном отображении.

Таким образом, внутренность квадрата, прямоугольника, эллипса – всё это элементарные области.

Пусть Ф – элементарная поверхность и G – элементарная область на плоскости, являющаяся образом Ф при гомеоморфизме.

Определение 3.2. Поверхностью F в пространстве называется множество точек пространства, которое можно покрыть конечным или счётным множеством элементарных поверхностей.

Из этого определения следует, что для любой точки M поверхности F существует элементарная поверхность Ф, такая, что , т.е. у каждой точки поверхности существует окрестность, являющаяся элементарной.

Введем понятие координат на поверхности.

Пусть на некоторой поверхности F задано однопараметрическое семейство линий, т.е. каждая линия этого семейства характеризуется определенным значением некоторого параметра. Назовем это семейство правильным, если через каждую точку поверхности проходит одна и только одна линия из данного семейства. Если на поверхности даны два правильных семей­ства, такие, что каждая из линий первого семейства пересекается без касания с каждой линией второго семейства не более чем в одной точке, то говорят, что на поверхности задана координат­ная сеть. Пусть линии первого из семейств, образующих коорди­натную сеть, определяются значениями некоторого параметра и. 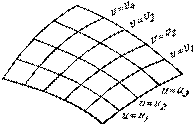А линии второго семейства – значениями некоторого параметра v. Так как по условию через каждую точку поверхности проходит единственная кривая из первого семейства и единственная кривая второго семейства, то положение точки на поверхности однозначно определяется соответствующими этим линиям значениями и₀ и v₀ параметров и и v (рис.6). Параметры и и v, значениями которых определяются линии, составляющие координатную сеть, называются координатами на данной поверхности.

Если на поверх­ности введены каким-либо образом координаты u, v,то говорят, что эта поверхность параметризована параметрами u и v. Каждая точка такой поверхности может быть задана значениями параметров u и v. Но эта же точка может быть задана и своими декартовыми координатами. Следовательно, декартовы координаты точек пара­метризованной поверхности представляют собой функции координат на поверхности.

Пусть u, v – декартовы координаты произвольной точки, принадлежащей , а x, y, z – координаты соответствующей точки поверхности. Тогда координаты x, y, z есть функции координат u, v при отображении f, т.е.

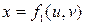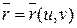, , . (3.1) Эту систему равенств, задающих отображение f области G в пространство, называют уравнениями поверхности в параметрической форме. Здесь u, v называются криволинейными координатами на поверхности. Параметрические уравнения (3.1) при фиксированных значениях u, v задают кривую, лежащую на поверхности. Будем также пользоваться векторной записью уравнения поверхности или .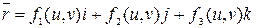

Последняя запись есть векторная функция двух скалярных аргументов u, v.

Замечание 3.1. Уравнение 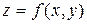можно рассматривать как частный случай параметрического уравнения, если принять x и y за параметры и положить .

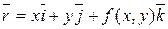В дальнейшем мы будем рассматривать поверхности, заданные именно параметрическими уравнениями, причем функцию 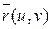будем предполагать непрерывной и имеющей непрерывные частные производ­ные по 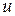и 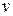. В некоторых случаях, нам придется потребовать также сущест­вования и непрерывности ее частных производных второго порядка.

 

Регулярная поверхность

Пусть Ф – элементарная поверхность, заданная уравнением .

Определение 3.3. Поверхность Ф называется регулярной (k раз дифференцируемой), если функции x, y, z имеют непрерывные, частные производные до порядка k включительно, причём в каждой точке 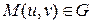ранг матрицы А = 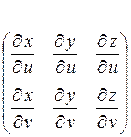равен двум.

При k = 1поверхность называется гладкой.

Замечание 3.2. Частные производные 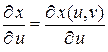, 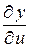и т.д. функций x, y, z будем обозначать . Таким образом, , .

Найдём частные производные радиус–вектора по u и v:

, .

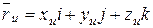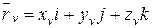Тогда матрица А примет вид A = 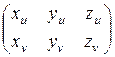и состоит из координат векторов и . Условие, что ранг A равен двум означает, что векторы и не коллинеарны. Далее будем рассматривать только такие векторы.

Как известно, из курса математического анализа, если функции x(u, v) и y(u, v) удовлетворяют условию 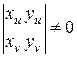, то вблизи данных значении u, v и соответствующих им значении x и y уравнения x=x(u, v) и y=y(u, v) могут быть разрешены относительно u, v. Таким образом, u=u(x, y), v=v(x, y) и получаем 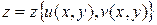или – уравнение поверхности в явном виде.

Кривые на поверхности

Рассмотрим на поверхности F множество точек, криволинейные координаты которых определяются уравнениями: u=u(t), v=v(t), где t – независимая переменная. Тогда векторная функция каждой точки поверхности может быть записана в виде: . При изменении параметра, вектор описывает своим концом некоторую кривую 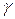в пространстве, тем самым кривую 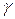на поверхности F.

В параграфе 3.1 построена, так называемая сеть кривых на поверхности или координатная сеть.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: