 |
Дросселирование. Эффект Джоуля-Томсона
|
|
|
|
Эффект падения давления потока рабочего тела в процессе преодоления им (потоком) местного сопротивления называется дросселированием.
Причинами возникновения местных сопротивлений при движении потока рабочего тела по каналам могут быть запорные, регулирующие и измерительные устройства; повороты, сужение, загрязнение каналов и т. д.
В процессе дросселирования изменение скорости га за или пара очень мало и можно принять скорость потока в сечении (I-I), расположенном до местного сопротивления, равной скорости потока в сечении (II-II) после местного сопротивления (рис. 6).
Рассмотрим процесс дросселирования, протекающий без внешней
работы (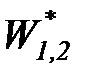 
= 0), в котором отсутствует теплообмен рабочего тела с внешней средой ( 
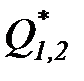= 0).
Падение давления за местным сопротивлением (рис. 6) обусловлено диссипацией (потерей) энергии потока, расходуемой на преодоление этого сопротивления, то есть на работу необратимых потерь ( 
).
Рис. 6. Схема процесса дросселирования газа или пара при
преодолении потоком местного сопротивления
Работа на преодоление сил трения, как известно, превращается в теплоту внутреннего теплообмена 
.
С учетом перечисленных условий рассматриваемого процесса дросселирования, уравнение первого начала термодинамики для потока по балансу рабочего тела
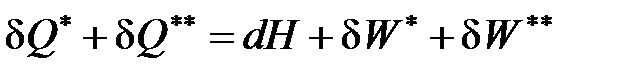(49)
примет вид
H2 - H1 = 0 или 
. (50)
Это значит, что рассматриваемый процесс дросселирования является процессом изоэнтальпийным: энтальпия рабочего тела до дросселя численно равна энтальпии рабочего тела после дросселя. При течении внутри дросселя энтальпия газа или пара меняется.
|
|
|
Если рассматривать в качестве местного сопротивления сужение канала, в суженном сечении поток ускоряется, кинетическая энергия увеличивается и энтальпия рабочего тела уменьшается (процесс 1 - 2') (рис. 7). После дросселя сечение потока вновь возрастает, поток тормозится, кинетическая энергия уменьшается, а энтальпия увеличивается до прежнего значения (процесс 2' - 2).
Процесс дросселирования является процессом необратимым; он всегда сопровождается ростом энтропии рабочего тела.
Явление изменения температуры газа или жидкости при адиабатном дросселировании называется эффектом Джоуля – Томсона.
Рис. 7. Процесс дросселирования в h-s диаграмме
Различают дифференциальный и интегральный дроссель – эффекты. Величина дифференциального дроссель – эффекта определяется из соотношения
, (51)
где 
– коэффициент дросселирования или коэффициент Джоуля – Томсона,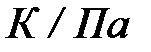 
.
Интегральный дроссель-эффект определяется по соотношению
. (52)
Коэффициент Джоуля – Томсона определяется из следующего уравнения, выведенного из математических выражений первого начала термодинамики и второго начала термостатики
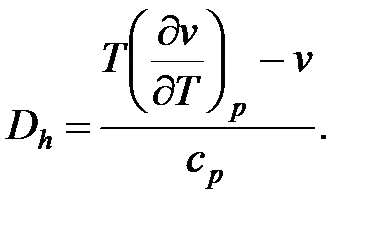(53)
Знак дифференциального дроссель–эффекта (коэффициента Джоуля – Томсона) определяется из анализа уравнения (53). В зависимости от характера изменения температуры T, имеют место три вида дроссель–эффекта (процесс дросселирования всегда происходит с падением давления dp< 0):
1. Дроссель–эффект положительный (Dh > 0), в этом случае процесс дросселирования сопровождается снижением температуры рабочего
тела (dT< 0);
2. Дроссель–эффект отрицательный (Dh < 0), в этом случае процесс дросселирования сопровождается повышением температуры рабочего тела (dT> 0);
|
|
|
3. Дроссель–эффект равен нулю (Dh = 0), если в процессе дросселирования температура рабочего тела не изменяется. Нулевой дроссель-эффект наблюдается при дросселировании идеального газа.
Как показывает опыт, для одного и того же вещества в зависимости от значений параметров состояния коэффициент Джоуля – Томсона Dh может иметь положительные, отрицательные значения, а также быть равным нулю.
Состояние газа или жидкости, которому соответствует условие Dh = 0, называется точкой инверсий. Геометрическое место точек инверсии на диаграмме состояния данного вещества называется кривой инверсии.
Кривая инверсии описывается уравнением
. (54)
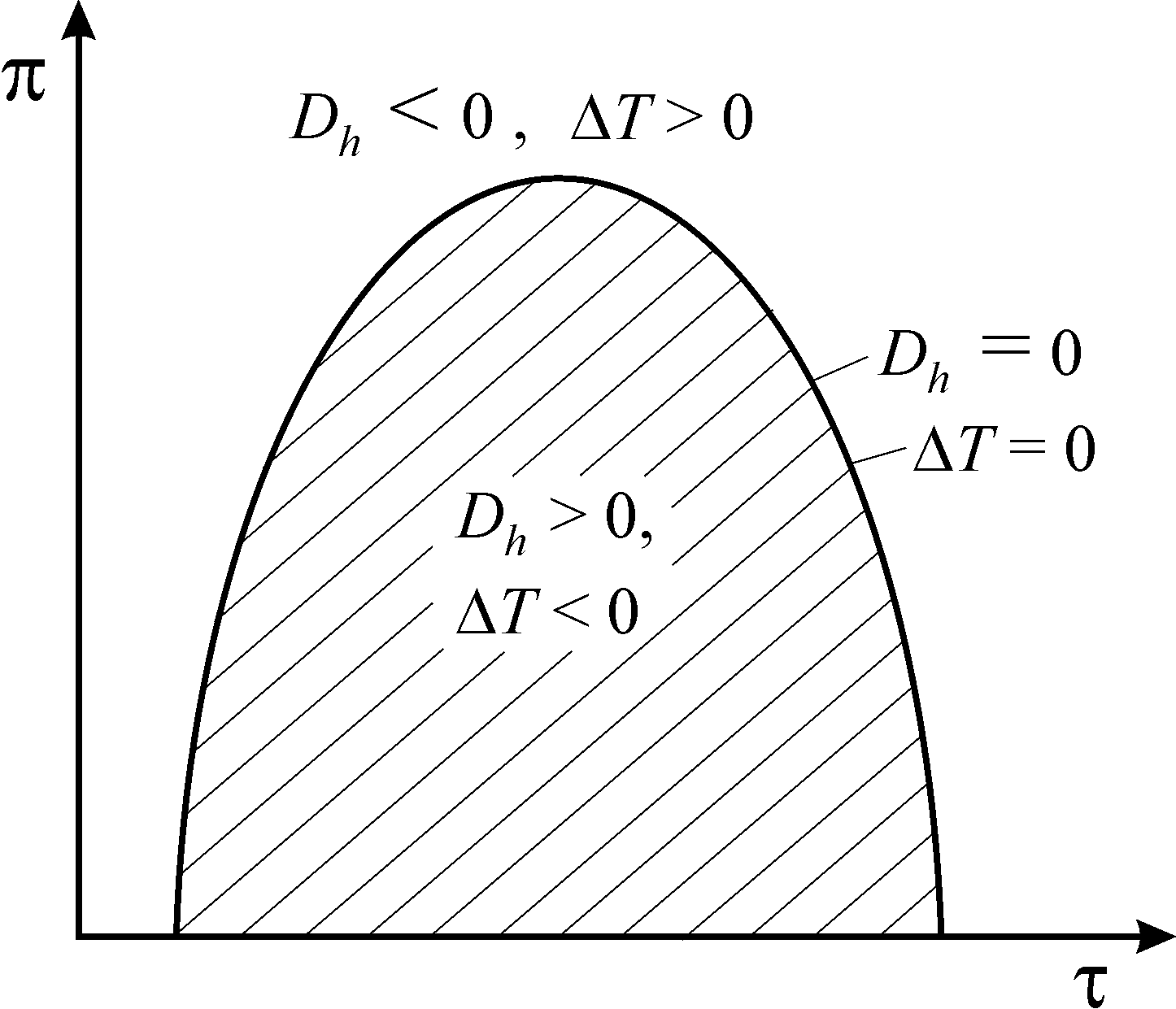
Для каждого вещества в диаграмме р - v имеется своя кривая инверсии. Закон соответственных состояний позволяет построить обобщенные кривые инверсии для групп термодинамически подобных веществ. Для природных газов инверсионная диаграмма приведена на графике в виде π = f(τ ) (рис. 8).
|
|
|
