 |
Второе начало термодинамики и его следствия. Принцип возрастания энтропии.
|
|
|
|
Второе начало термодинамики и его следствия. Принцип возрастания энтропии.
Все явления природы, связанные с превращением энергии имеют необратимый характер. Обобщающим законом необратимости процессов в природе является принцип возрастания энтропии изолированных систем. В основу второго начала термодинамики положен постулат, утверждающих необратимость реальных процессов и имеющий ряд равнозначных формулировок:
· теплота не может самопроизвольно передаваться от холодного тела к более нагретому (Р. Клаузиус, 1850 г. );
· невозможно построить периодически действующую машину, вся деятельность которой сводилась бы к выполнению механической работы и охлаждению теплового источника (В. Томсон – Кельвин, 1852 г. );
· любой реальный самопроизвольный процесс является необратимым
(М. Планк, 1926 г. );
· работа может быть непосредственно и полностью превращена в теплоту путем трения или электронагрева.
Эти формулировки подчеркивают специфичность теплоты при ее превращениях. В теплоту полностью превращаются все виды энергии. Превращения же теплоты всегда сопровождаются процессами, компенсирующими эти превращения. В тепловом двигателе такой компенсацией является передача некоторой части теплоты источнику низшей температуры (холодному источнику); в холодильных машинах такой компенсацией являются затраты работы.
Анализ различных формулировок постулата второго начала термодинамики приводит к некоторым весьма важным следствиям.
Следствие I. Невозможно осуществление полного превращения теплоты работу, т. е. нельзя создать вечный двигатель второго рода (Perpetuum
mobile II рода) с коэффициентом полезного действия равным единице.
|
|
|
Это следствие вытекает из постулата в формулировке Томсона-Кельвина, согласно которой всякий тепловой двигатель должен иметь как минимум два источника теплоты с различной температурой Т1 и Т2. Следовательно, всегда ú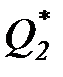 
ç > 0 и поэтому
. (40)
Следствие II. КПД реального теплового двигателя и холодильный коэффициент реальной холодильной машины, в которых осуществляются циклы при температурах внешних источников Т1 и Т2, всегда меньше КПД и холодильного коэффициента обратимых тепловых машин, циклы в которых осуществляются между теми же внешними источниками:
h < hобр ; c < cобр . (41)
Снижение КПД и холодильного коэффициента реальных тепловых машин по сравнению с hобр и cобр обратимой тепловой машины обусловлено прямым превращением части работы в теплоту (необратимые потери работы) и наличием конечной разности температур между внешними источниками теплоты и рабочим телом.
Следствие III. Абсолютный нуль по термодинамической абсолютной шкале температур (шкала Кельвина) недостижим (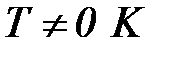 
).
Это следствие вытекает из анализа соотношения по определению КПД цикла Карно (34) и постулата второго начала термодинамики в формулировке Томсона-Кельвина. Поскольку КПД любого теплового двигателя и даже работающего по эталонному циклу Карно всегда меньше 1
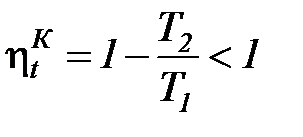, (42)
и в случае, если горячий источник теплоты имеет положительную температуру по термодинамической абсолютной шкале температур ( 
), справедливо утверждение
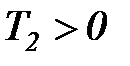. (43)
Математическое выражение второго начала термодинамики
Наиболее наглядно принцип возрастания энтропии доказывается на основе изучения круговых процессов тепловых машин.
|
|
|
Рассмотрим реальный процесс 1-2 на диаграмме Т-S (рис. 8).
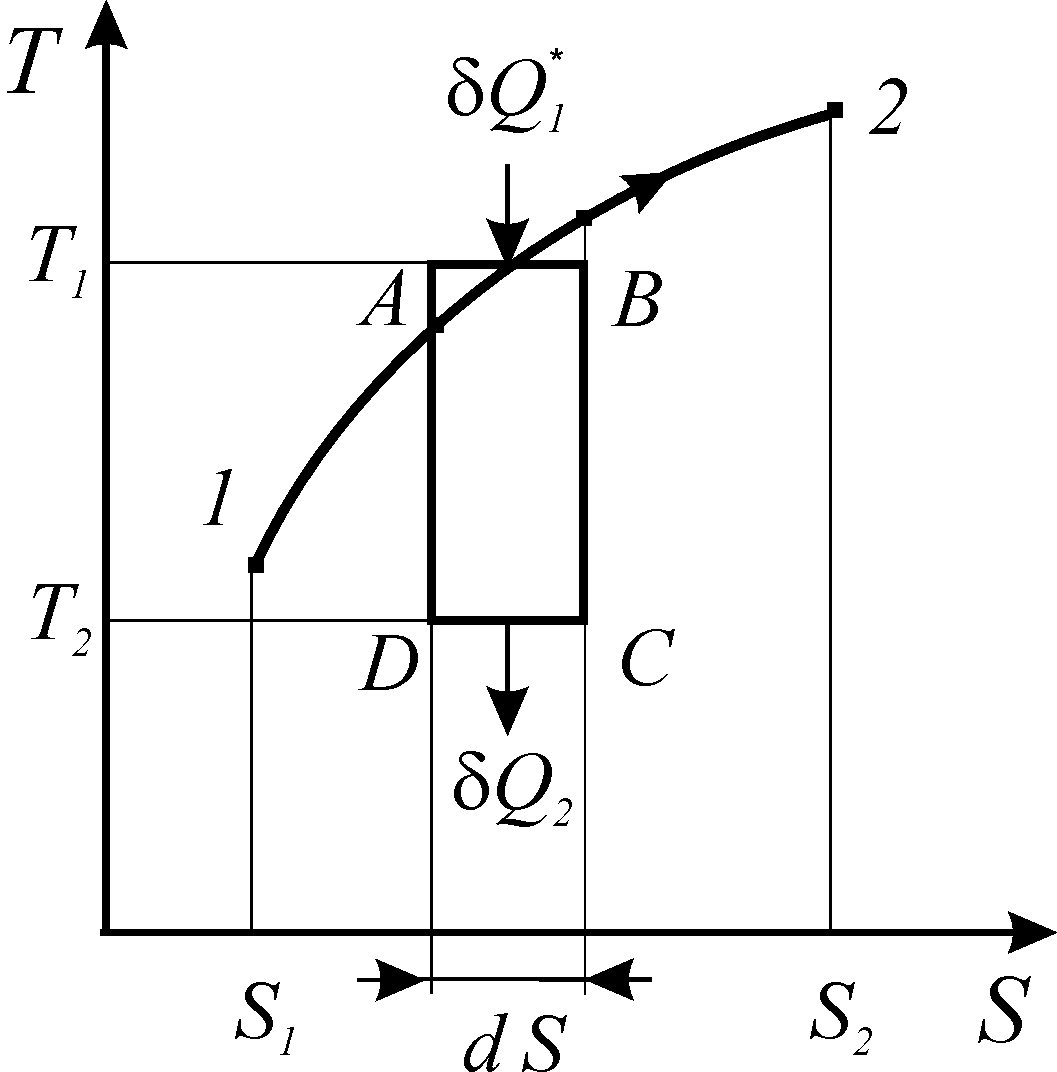
| Рис. 8. К доказательству второго начала термодинамики |
Выделим на кривой процесса элементарный участок А-В и к нему добавим три обратимых процесса: адиабату расширения В-С, изотерму отвода теплоты С-D и адиабату сжатия D-А. Полученный цикл А-В-С-D, в целом, необратим из-за реального процесса 1-2, а следовательно его КПД меньше, чем у цикла Карно
. (44)
В выражении (44) справедлив знак неравенства, если рассматриваемый цикл (А-В-С-D) необратим, и знак равенства, если рассматривается обратимый цикл.
После преобразования выражения (44), для любых циклов получаем:
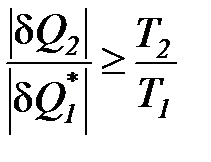; (45)
; (46)
. (47)
Учитывая то, что количество теплоты, подведенной к рабочему телу извне, имеет положительный знак ( 
), а количество теплоты,
отведенной от рабочего тела – отрицательно (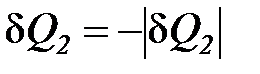 
), из
выражения (47) получаем следующее неравенство
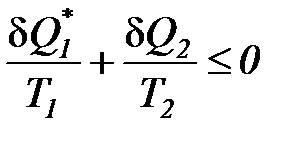. (48)
Для рабочего тела в обратимом процессе CD согласно II началу термостатики
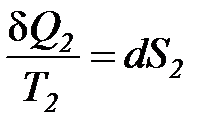. (49)
Согласно условию замыкания кругового процесса (A-B-C-D-A), интегральное изменение любой функции состояния рабочего тела равно нулю, а, так как энтропия изменяется только в процессах A-B и C-D, это условие можно представить следующим образом:
. (50)
Выражение (48) с учетом соотношений (49), (50) приобретает следующий вид:
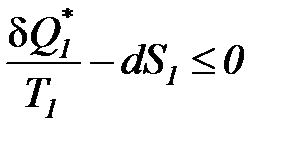(51)
или
. (52)
Вследствие того, что при выводе рассматривался произвольный процесс и не было ограничений на свойства рабочего тела, результаты вывода имеют самый общий характер.
Итоговое математическое выражение второго начала термодинамики в дифференциальной и интегральной формах, как принципа возрастания энтропии изолированных систем имеет следующий вид:
; (53)
. (54)
|
|
|
Знак неравенства в выражениях (53), (54) справедлив в случае, когда в системе происходят реальные необратимые процессы, а равенства – при протекании обратимых процессов.
Если совместить математические выражения второго начала термостатики (34) и второго начала термодинамики (53) то получается следующее соотношение:
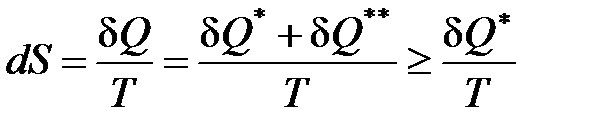, (55)
из которого вытекает следующее утверждение:
dS** =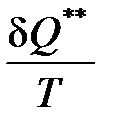 
> 0, ( 56)
а при условии, что абсолютная температура всегда положительна (T > 0), непосредственно следует принцип необратимости внутреннего теплообмена
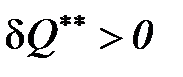. 57 (57)
Данное неравенство (57) свидетельствует о том, что внутренний теплообмен dQ** в реальных процессах имеет только положительный знак, т. е. работа и количество теплоты в действительных процессах всегда меньше работы и теплоты в обратимом процессе. Затраты работы на необратимые потери в реальных процессах, равные количеству теплоты внутреннего теплообмена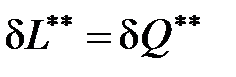 
, однозначно способствуют росту энтропии.
Для изолированной системы, у которой отсутствует теплообмен с окружающей средой ( 
), неравенства (53), (54) принимают вид
dSизол ³ 0, S2 ³ S2. 58 (58)
Анализ выражения (58) наглядно показывает, что какие бы процессы не протекали в изолированной системе, ее энтропия не может уменьшаться. При протекании в изолированной системе необратимых процессов энтропия системы возрастает; если же в ней протекают обратимые процессы, то энтропия системы остается неизменной.
|
|
|
