 |
Общие соотношения. Истечение несжимаемых жидкостей
|
|
|
|
Общие соотношения
При обратимых процессах истечения жидкости из области большего давления р1 в область с меньшим давлением р2, потенциальная работа расходуется на повышение кинетической энергии и на изменение высоты центра тяжести потока (рис. 1. ).
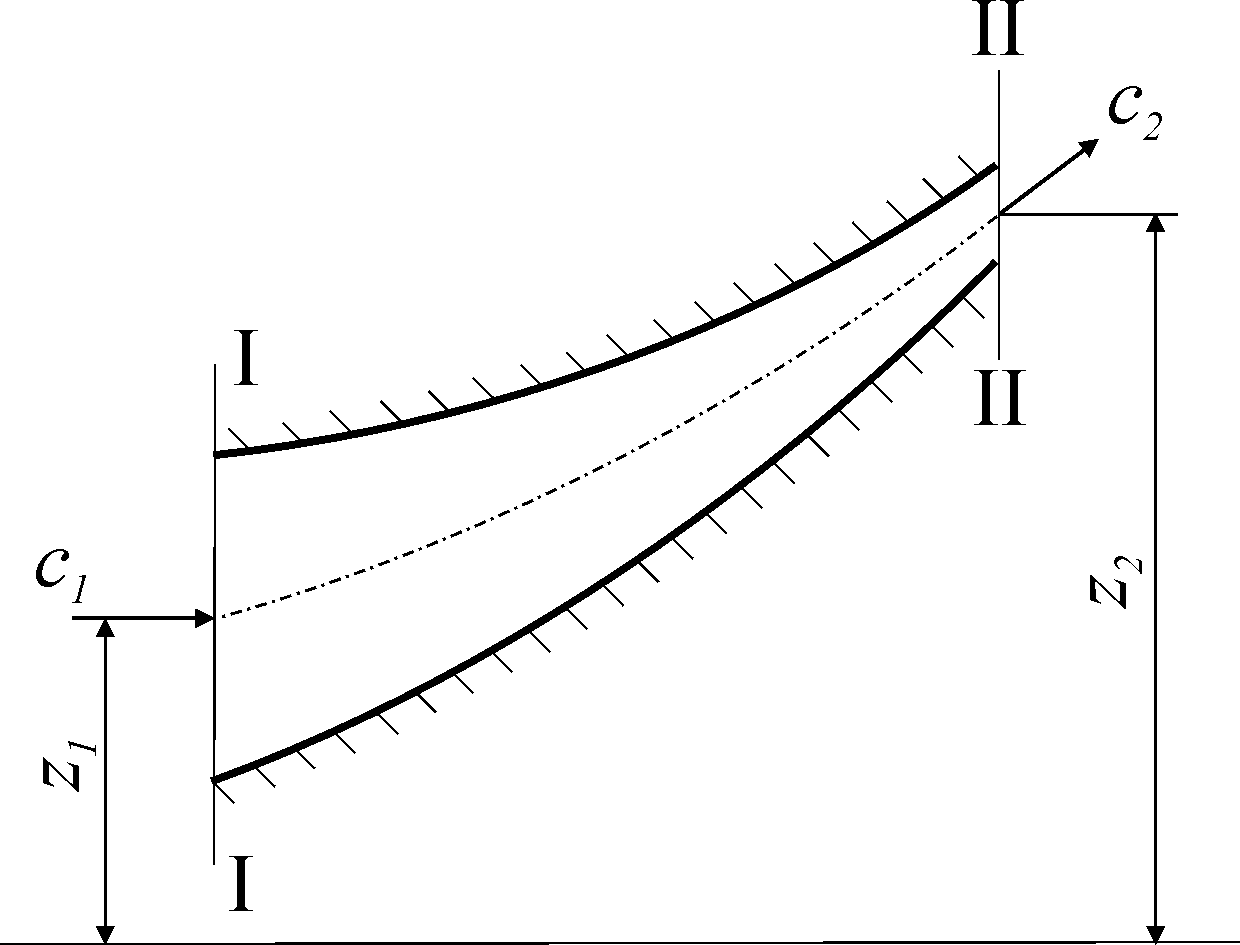
Рис. 1. Истечение жидкости, газа или пара из сопла
При адиабатном процессе истечения справедливо следующее соотношение:
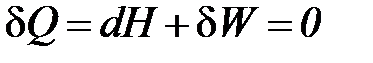. (1. )
Дифференциальное уравнение распределения удельной потенциальной работы, при отсутствии эффективной потенциальной работы потока (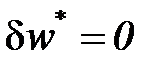 
), будет выглядеть следующим образом:
. (2)
Уравнение распределения потенциальной работы в конечном процессе
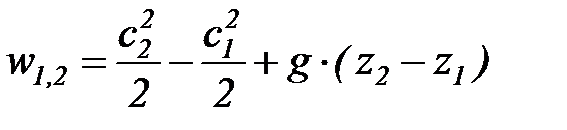(3)
дает возможность получить соотношение для определения теоретической линейной скорости истечения жидкости в выходном сечении сопла (с2)
. (4)
Сопла или штуцеры, через которые происходят процессы истечения, обычно выполняются короткими, поэтому работой, идущей на изменение центра тяжести потока 
, можно пренебречь. При этом условии теоретическая линейная скорость истечения жидкости в выходном сечении сопла может быть определена из соотношения
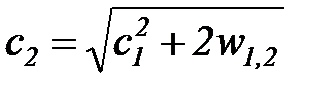. (5)
Скорость потока на входе в сопло может быть вычислена, в свою очередь, как теоретическая скорость истечения из воображаемого нулевого состояния (точка 0), в котором жидкость находится в состоянии покоя (с0=0), до заданного начального состояния (1) (рис. 2). Параметры нулевой точки р0, v0, T0, h0, называются параметрами адиабатно заторможенного потока.
|
|
|
Состояние адиабатно заторможенного потока находится графически на продолжении кривой процесса истечения в точке (0). Площадь между кривой процесса (0-1) и осью ординат (1-0-а-b) равна потенциальной работе в процессе 0-1 (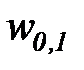 
) (рис. 2).
По аналогии с соотношением (5), линейная скорость потока во входном сечении сопла определяется по формуле
. (6)
Рис. 2. Процесс истечения газа в в p-v диаграмме
Подставив выражение (6) в соотношение (5), получаем
. (7)
Сумма потенциальных работ w0, 1 и w1, 2, представляет собой потенциальную работу жидкости (сжимаемой или несжимаемой) в обратимом адиабатном процессе истечения от нулевого состояния (с0 =0), определяемого параметрами торможения, до конечного давления p2 ( 
).
Следовательно, соотношение для определения линейной теоретической скорости обратимого адиабатного процесса истечения жидкости можно записать следующим образом
. (8)
Важной характеристикой потока является его массовая скорость, численно равная секундному расходу жидкости через единицу площади поперечного сечения потока ( 
, кг/(м2× с))
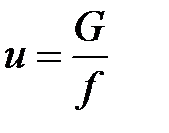. (9)
Связь между массовой и линейной скоростью потока определяется соотношением
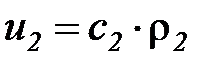. (10)
В соответствии с принципом неразрывности потока, массовый расход вещества (G) в любом поперечном сечении канала одинаков
. (11)
Истечение несжимаемых жидкостей
Несжимаемая жидкость имеет практически неизменную плотность при любых давлениях и температурах ( 
). Соотношения для определения удельной потенциальной работы несжимаемой жидкости в обратимых процессах истечения (1-2, 0-2) имеют следующий вид:
|
|
|
; 
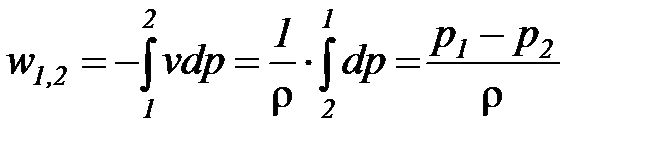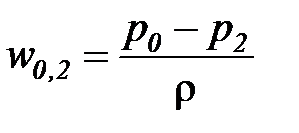. (12)
С учетом соотношений (12), теоретическая линейная скорость истечения несжимаемой жидкости в выходном сечении сопла (с2) может быть определена из следующих соотношений:
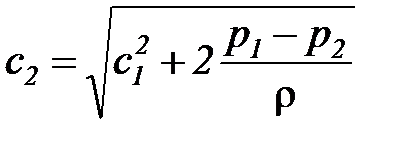; (13)
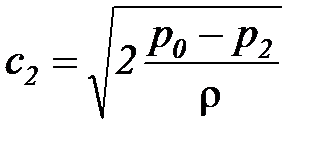. (14)
Массовая скорость потока несжимаемой жидкости на выходе из сопла, в соответствии с уравнением (10), находится по формуле
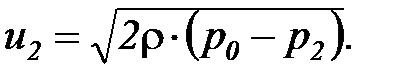(15)
Из соотношения (15) видно, что с увеличением по длине канала (x) разности давления (р0 - рx), повышается массовая скорость потока. При этом, исходя из принципа неразрывности потока (G = idem), площадь проходного сечения канала 
, должна непрерывно уменьшаться. Следовательно, при истечении несжимаемой жидкости следует применять суживающиеся сопла.
|
|
|
