 |
Истечение сжимаемых жидкостей
|
|
|
|
К классу сжимаемых жидкостей относятся вещества, плотность которых изменяется в зависимости от давления и температуры. Газы (идеальные и реальные) относятся к классу сжимаемых жидкостей.
Потенциальная работа обратимого адиабатного процесса истечения газа от нулевого до конечного состояния (0-2) находится из соотношения
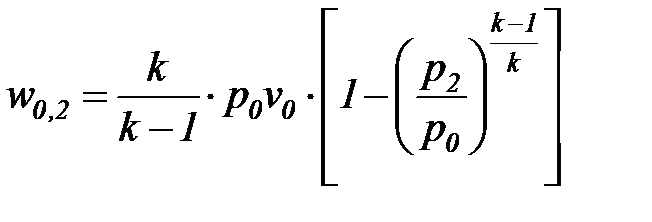. (16)
После подстановки выражения (16) в соотношение (8) получаем формулу для расчета скорости истечения газа в выходном сечении сопла
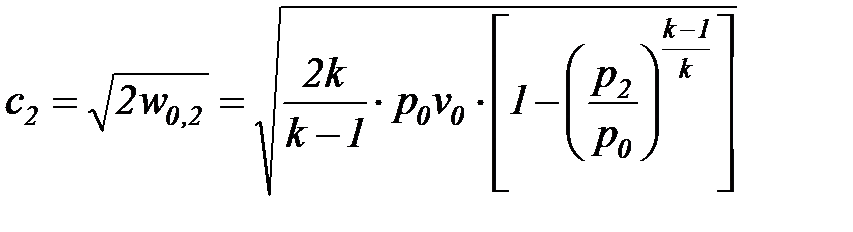. (17)
Для вычисления массовой скорости газа по уравнению ( 
) необходимо знать плотность газа в выходном сечении сопла ( 
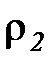), значение которой определяется из уравнения адиабаты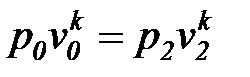 
. (18)
После ряда несложных преобразований получим соотношение для расчета массовой скорости газа в выходном сечении сопла
. (19)
Введем в уравнение (19) коэффициент расхода λ
(20)
и получим следующее соотношение для определения массовой скорости газа на выходе из сопла
. (21)
Анализ уравнения (19) для массовой скорости потока показывает, что скорость газа изменяясь в зависимости от соотношения давлений в процессе истечения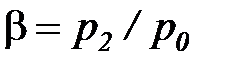 
, дважды обращается в нуль - при р2/р0 = 1 (нет движения), а также при 
= 0 (истечение в вакуум, р2 = 0). Следовательно, значение массовой скорости, по теореме Ролля, проходит через экстремум (рис. 3). Соотношение давлений, при котором массовая скорость истечения становится максимальной (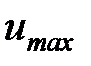 
), называется критическим ( 
), а режим истечения при этом условии называется критическим режимом истечения.
|
|
|
Рис. 3. Зависимость линейной и массовой скоростей истечения
газа от соотношения давлений в процессе истечения 
Для определения характеристик критического режима истечения обозначим через ψ члены уравнения (19), зависящие от величины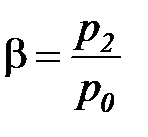 
(остальные члены зависят лишь от параметров исходного состояния и природы газа)
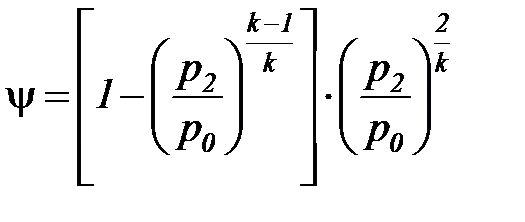. (22)
Введем в уравнение (22) дополнительно характеристику адиабатного расширения газа
. (23)
Тогда
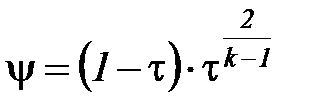, (24)
так как
. (25)
Очевидно, что массовая скорость достигнет максимального значения при таком же β кр, что и функция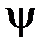 
. Условием максимума функции 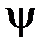является
. (26)
Исходя из соотношения (26), после преобразования, находим критическое значение характеристики адиабатного расширения сжимаемых жидкостей при истечении ( 
) и критическое соотношение давлений (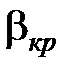 
):
; (27)
. (28)
Подставив выражение (27) в соотношение (17), получим выражение для расчета критической линейной скорости истечения
. (29)
С учетом того, что справедливо следующее выражение
, (30)
получаем следующие соотношения для расчета критической линейной скорости истечения:
; (31)
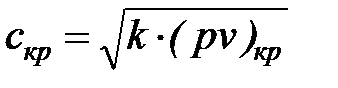, (32)
где 
– потенциальная функция сжимаемой жидкости в сечении сопла, где наблюдается критическая скорость истечения (27), (30).
Для обратимого адиабатного истечения любой сжимаемой жидкости критическая линейная скорость равна местной скорости звука в данной среде
|
|
|
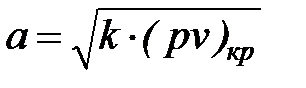. (33)
Значение массовой критической скорости истечения определяется из соотношения
. (34)
Коэффициент расхода λ кр при критическом режиме истечения находится при подстановке выражений (27) и (28) в соотношение (29)
. (35)
Итоговое выражение для определения коэффициента расхода в критическом режиме истечения λ кр имеет следующий вид:
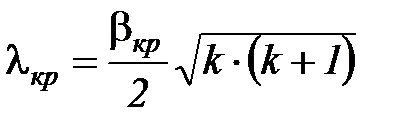. (36)
Процессы истечения газа и паров в суживающихся соплах или через отверстия в тонких стенках имеют целый ряд особенностей. Одной из особенностей процессов истечения газа и паров в суживающихся соплах или через отверстия в тонких является невозможность реализации закритического режима истечения.
На рис. 3 приведены графические зависимости изменения линейной (с) и массовой (u) скоростей истечения несжимаемых жидкостей от соотношения давлений в процессе истечения .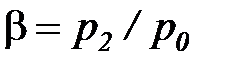
Область диаграммы, в которой 
называется областью докритического режима истечения. В этой области давление потока в выходном сечении сопла (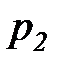 
) равно давлению среды ( 
), в которую происходит истечение ( 
), а при снижении давления среды ( ) наблюдается увеличение массового расхода через сопло (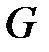 
), а также линейной ( 
) и массовой ( 
) скорости потока в выходном сечении сопла (рис. 1).
После достижения критического соотношения давлений (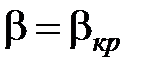 
) наступает критический режим истечения, при котором на выходе из сопла устанавливается критическое давление режима ( 
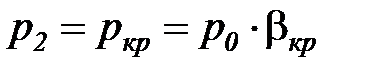). Этот режим характеризуется критическими значениями массового расхода ( 
), линейной ( 
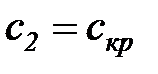) и массовой ( 
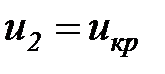) скорости истечения в выходном сечении сопла.
Дальнейшее снижение давления среды ( ), в которую происходит истечение вещества, не приводит к снижению давления на выходе из сопла, которое остается неизменным и равным критическому давлению ( 
).
Это явление называется «кризисом течения». В критическом режиме истечения скорость потока в выходном сечении сопла устанавливается равной местной скорости звука в данной среде (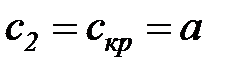 
). С этой же скоростью (скоростью звука) в среде распространяется любое возмущение. Установившаяся в выходном сечении сопла критическая скорость истечения ( 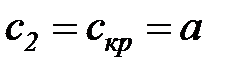) препятствует подходу волны разряжения к этому сечению сопла, что и предопределяет стабилизацию линейной скорости истечения на уровне критического значения даже при дальнейшем снижении давления среды. При данных условиях истечения ( 
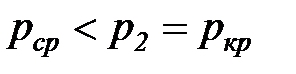) для увеличения кинетической энергии потока используется не весь располагаемый перепад давления ( 
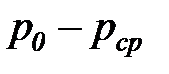), а только часть его ( 
).
|
|
|
Таким образом, при истечении через суживающиеся сопла и отверстия в тонких стенках возможны только два режима истечения - докритический и критический. Процесс истечения через суживающиеся сопла и отверстия в тонких стенках возможен только при выполнении следующего условия:
. (37)
Для обеспечения закритического режима истечения, характеризующегося условием ( 
), необходимо дополнить суживающееся сопло расширяющейся частью, в выходном сечении которой возможно достичь значения давления ниже критического ( 
). Такое комбинированное сопло называется соплом Лаваля.
В комбинированных соплах для увеличения кинетической энергии потока может использоваться весь располагаемый перепад давления ( ).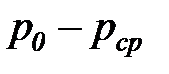
Переход от выражений теоретических скоростей истечения (с2, u2) к реальным их значениям (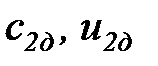 
) осуществляется с помощью коэффициентов скорости φ и расхода μ , определяемых опытным путем (значения φ и μ меньше единицы)
; 
. (38)
Процессы истечения паров и, в частности, водяного пара в ряде слуаев рассчитываются с использованием h-s диаграмм (рис. 4).
Рис. 4. Процесс истечения водяного пара в h-s диаграмме
В обратимом адиабатном процессе из первого начала термодинамики при 
следует, что 
.
Используя уравнения первого начала термодинамики и распределения потенциальной работы (2) и учитывая, что для коротких насадок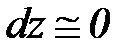 
, получим следующие соотношения:
если рассматривать процесс истечения (1-2) (рис. 4)
, (39)
|
|
|
если же рассматривать истечение в процессе (0-1)
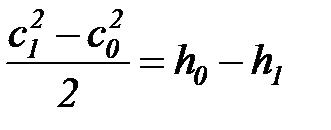(40)
или
. (41)
В обратимом адиабатном процессе истечения (0-2) скорость в выходном сечении сопла может быть определена из соотношения
. (42)
Разность энтальпий между сечениями 0 и 2 (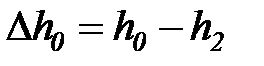 
) называется раcполагаемым теплоперепадом.
В реальных процессах истечения при наличии необратимых потерь работы, действительная скорость истечения (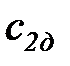 
) будет несколько меньше и может быть определена из соотношения 
или найдена с использованием внутреннего КПД сопла ( 
).
Для определения внутреннего КПД сопла ( 
) следует оценить величину работы необратимых потерь в действительных процессах истечения.
Работа необратимых потерь, обусловленная трением и завихрениями в реальном процессе истечения, может быть выражена соотношением
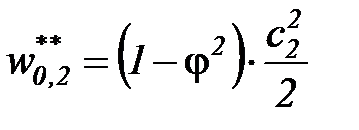, (43)
где 
– коэффициент потери энергии.
Работа необратимых потерь превращается в теплоту внутреннего теплообмена
, (44)
что приводит к увеличению значения энтальпии пара на выходе из сопла в действительном процессе истечения по сравнению с обратимым адиабатным процессом
(45)
и снижению действительной скорости истечения по сравнению с теоретической
. (46)
Таким образом, работа необратимых потерь, обусловленная трением и завихрениями в реальном процессе истечения, обуславливает отклонение реального процесса истечения от обратимого адиабатного процесса в сторону возрастания энтропии (рис. 4).
Разность энтальпий в реальном процессе истечения (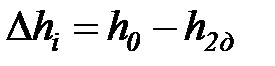 
) называется действительным теплоперепадом.
Степень совершенства действительного процесса истечения пара характеризуется внутренним КПД сопла (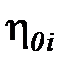 
)
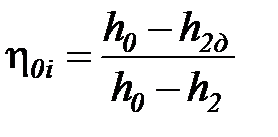. (47)
Внутренний КПД сопла ( 
) используется для определения действительной скорости истечения паров на выходе из сопла
. (48)
|
|
|
