 |
Основные идеи вычислительного метода динамического программирования
|
|
|
|
Глава 4. Динамическое программирование
Некоторые задачи математического программирования обладают характерными особенностями, которые позволяют свести их решение к рассмотрению некоторого множества более простых «подзадач». В результате вопрос о глобальной оптимизации некоторой функции сводится к поэтапной оптимизации некоторых промежуточных целевых функций. В динамическом программировании рассматриваются методы, позволяющие путем поэтапной (многошаговой) оптимизации получить общий (результирующий) оптимум.
Обычно методами динамического программирования оптимизируют работу некоторых управляемых систем, эффект которой оценивается аддитивной, или мультипликативной, целевой функцией. Аддитивной называется такая функция нескольких переменных 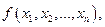 значение которой вычисляется как сумма некоторых функций
значение которой вычисляется как сумма некоторых функций 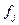 , зависящих только от одной переменной
, зависящих только от одной переменной 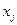
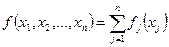 . (1)
. (1)
Слагаемые аддитивной целевой функции соответствуют эффекту решений, принимаемых на отдельных этапах управляемого процесса. По аналогии, мультипликативная функция распадается на произведение положительных функций различных переменных:
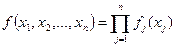 . (2)
. (2)
Поскольку логарифм функции типа (2) является аддитивной функцией, достаточно ограничиться рассмотрением функций вида (1).
Изложим сущность вычислительного метода динамического программирования на примере задачи оптимизации
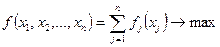 , (3)
, (3)
при ограничениях
 . (4)
. (4)
В отличие от задач, рассмотренных ранее, о линейности и дифференцируемости функций 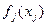 не делается никаких предположений, поэтому применение классических методов оптимизации (например, метода Лагранжа) для решения задачи (3)-(4) либо проблематично, либо просто невозможно.
не делается никаких предположений, поэтому применение классических методов оптимизации (например, метода Лагранжа) для решения задачи (3)-(4) либо проблематично, либо просто невозможно.
|
|
|
Содержательно задача (3)-(4) может быть интерпретирована как проблема оптимального вложения некоторых ресурсов j, приводимых к единой размерности (например, денег) с помощью коэффициентов  в различные активы (инвестиционные проекты, предприятия и т. п.), характеризующиеся функциями прибыли
в различные активы (инвестиционные проекты, предприятия и т. п.), характеризующиеся функциями прибыли 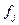 , т. е. такого распределения ограниченного объема ресурса (b), которое максимизирует суммарную прибыль.
, т. е. такого распределения ограниченного объема ресурса (b), которое максимизирует суммарную прибыль.
Рассмотрим ситуацию, когда она решается последовательно для каждого актива. Если на первом шаге принято решение о вложении в п- йактив 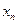 единиц, то на остальных шагах мы сможем распределить
единиц, то на остальных шагах мы сможем распределить 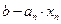 единиц ресурса. Абстрагируясь от соображений, на основе которых принималось решение на первом шаге (допустим, мы по каким-либо причинам не могли на него повлиять), будет вполне естественным поступить так, чтобы на оставшихся шагах распределение текущего объема ресурса произошло оптимально, что равнозначно решению задачи
единиц ресурса. Абстрагируясь от соображений, на основе которых принималось решение на первом шаге (допустим, мы по каким-либо причинам не могли на него повлиять), будет вполне естественным поступить так, чтобы на оставшихся шагах распределение текущего объема ресурса произошло оптимально, что равнозначно решению задачи
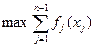 (5)
(5)
при ограничениях
 . (6)
. (6)
Очевидно, что максимальное значение (5) зависит от размера распределяемого остатка, и если оставшееся количество ресурса обозначить через  , то величину (5) можно выразить как функцию от
, то величину (5) можно выразить как функцию от  :
:
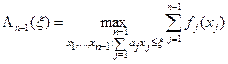 , (7)
, (7)
где индекс 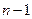 указывает на оставшееся количество шагов. Тогда суммарный доход, получаемый как следствие решения, принятого на первом шаге, и оптимальных решений, принятых на остальных шагах, будет
указывает на оставшееся количество шагов. Тогда суммарный доход, получаемый как следствие решения, принятого на первом шаге, и оптимальных решений, принятых на остальных шагах, будет
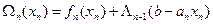 . (8)
. (8)
Если бы имелась возможность влиять на 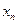 , то для получения максимальной прибыли необходимо было максимизировать
, то для получения максимальной прибыли необходимо было максимизировать  по переменной
по переменной 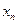 , т. е. найти
, т. е. найти 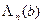 и фактически решить задачу:
и фактически решить задачу:
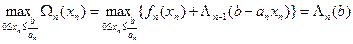 . (9)
. (9)
В результате получим выражение для значения целевой функции задачи при оптимальном поэтапном процессе принятия решений о распределении ресурса. Это значение в силу построения данного процесса равно глобальному оптимуму целевой функции
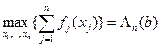 , (10)
, (10)
т. е. значению целевой функции при одномоментном распределении ресурса.
Если в выражении (9) заменить значения b на  ,и п на k, то его можно рассматривать как рекуррентную формулу, позволяющую последовательно вычислять оптимальные значения целевой функции при распределении объема ресурса
,и п на k, то его можно рассматривать как рекуррентную формулу, позволяющую последовательно вычислять оптимальные значения целевой функции при распределении объема ресурса  за k шагов:
за k шагов:
|
|
|
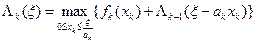 . (11)
. (11)
Значение переменной  , при котором достигается рассматриваемый максимум, обозначим
, при котором достигается рассматриваемый максимум, обозначим 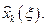 При
При  формула (11) принимает вид
формула (11) принимает вид
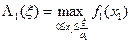 , (12)
, (12)
т. е. допускает непосредственное вычисление функций 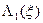 и
и 
Используя (12) как основание рекурсии, можно с помощью (11) последовательно вычислить  и
и 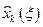 ,
, 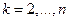 . Положив на последнем шаге
. Положив на последнем шаге 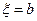 , в силу (9), найдем глобальный максимум функции (3), равный
, в силу (9), найдем глобальный максимум функции (3), равный 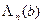 , и компоненту оптимального плана
, и компоненту оптимального плана  . Полученная компонента позволяет вычислить нераспределенный остаток на следующем шаге при оптимальном планировании:
. Полученная компонента позволяет вычислить нераспределенный остаток на следующем шаге при оптимальном планировании: 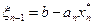 ,и, в свою очередь, найти
,и, в свою очередь, найти  . В результате подобных вычислений последовательно будут найдены все компоненты оптимального плана.
. В результате подобных вычислений последовательно будут найдены все компоненты оптимального плана.
Таким образом, динамическое программирование представляет собой целенаправленный перебор вариантов, который приводит к нахождению глобального максимума. Уравнение (11), выражающее оптимальное решение на k -м шаге через решения, принятые на предыдущих шагах, называется основным рекуррентным соотношением динамического программирования. В то же время следует заметить, что описанная схема решения при столь общей постановке задачи имеет чисто теоретическое значение, так как замыкает вычислительный процесс на построение функций 
 , т. е. сводит исходную задачу (3)-(4) к другой весьма сложной проблеме. Однако при определенных условиях применение рекуррентных соотношений может оказаться весьма плодотворным. В первую очередь это относится к задачам, которые допускают табличное задание функций
, т. е. сводит исходную задачу (3)-(4) к другой весьма сложной проблеме. Однако при определенных условиях применение рекуррентных соотношений может оказаться весьма плодотворным. В первую очередь это относится к задачам, которые допускают табличное задание функций  .
.
|
|
|


