 |
Задачи динамического программирования,
|
|
|
|
Допускающие табличное задание рекуррентных соотношений
Рассмотрим процесс решения модифицированного варианта задачи (3)-(4), в котором переменные 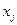 и параметры
и параметры  могут принимать только целочисленные значения, а ограничение (4) имеет вид равенства. В рамках предложенной интерпретации о вложении средств в активы данные предпосылки вполне реалистичны и, более того, могут быть даже усилены требованием о кратности значений
могут принимать только целочисленные значения, а ограничение (4) имеет вид равенства. В рамках предложенной интерпретации о вложении средств в активы данные предпосылки вполне реалистичны и, более того, могут быть даже усилены требованием о кратности значений 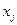 ,например, 1000 единицам.
,например, 1000 единицам.
Чтобы не усложнять обозначения, условимся операции целочисленной арифметики записывать стандартным образом, полагая, что промежуточные результаты подвергаются правильному округлению. Так, например, будем считать, что 12/5 = 2.
В соответствии с общей схемой вычислительного алгоритма на первом шаге необходимо построить функцию
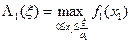 .
.
Поскольку  ,
, 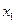 принимает конечное число целых значений от 0 до
принимает конечное число целых значений от 0 до  . Это позволяет, например, путем перебора значений
. Это позволяет, например, путем перебора значений  найти функцию
найти функцию 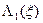 и задать ее в форме таблицы следующей структуры (табл. 5.1).
и задать ее в форме таблицы следующей структуры (табл. 5.1).
Последняя колонка табл. 5.1  содержит значение
содержит значение  , на котором достигается оптимальное решение первого шага. Его необходимо запоминать для того, чтобы к последнему шагу иметь значения всех компонент оптимального плана.
, на котором достигается оптимальное решение первого шага. Его необходимо запоминать для того, чтобы к последнему шагу иметь значения всех компонент оптимального плана.
На следующем (втором) шаге приступаем к вычислению функции  , значения которой для каждого отдельно взятого
, значения которой для каждого отдельно взятого 
 находятся как
находятся как
 ,
,
где значения

берутся из табл. 5.1. В результате вычислений формируется таблица значений  , содержащая на одну колонку больше по сравнению с табл. 5.1, так как теперь необходимо запомнить оптимальные решения первого
, содержащая на одну колонку больше по сравнению с табл. 5.1, так как теперь необходимо запомнить оптимальные решения первого  и второго шагов
и второго шагов  .
.

| 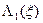
| 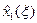
|
| … | … | … |
| B |
Таблица 5.1
На последующих шагах с номером  осуществляются аналогичные действия, результатом которых становятся таблицы значений
осуществляются аналогичные действия, результатом которых становятся таблицы значений  ,где
,где  (табл. 5.2).
(табл. 5.2).
|
|
|

| 
| 
| … | 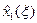
|
| … | … | … | ||
| b |
Таблица 5.2
На последнем п- омшаге нет необходимости табулировать функцию 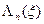 , так как достаточно определить лишь
, так как достаточно определить лишь  . Одновременно определяется и оптимальное значение n -й компоненты оптимального плана
. Одновременно определяется и оптимальное значение n -й компоненты оптимального плана  . Далее, используя таблицу, сформированную на предыдущем шаге, определяем оптимальные значения остальных переменных:
. Далее, используя таблицу, сформированную на предыдущем шаге, определяем оптимальные значения остальных переменных:

и т. д. или, в общем виде,
 . (13)
. (13)
Следует подчеркнуть одно из преимуществ описанного метода с точки зрения его практической реализации в рамках программного обеспечения для ЭВМ: на каждом шаге алгоритма непосредственно используется только таблица, полученная на предыдущем шаге, т. е. нет необходимости сохранять ранее полученные таблицы. Последнее позволяет существенно экономить ресурсы компьютера.
Выигрыш, который дает применение рассмотренного алгоритма, может также быть оценен с помощью следующего простого примера. Сравним приблизительно по числу операций (состоящих, в основном, из вычислений целевой функции) описанный метод с прямым перебором допустимых планов задачи (3)-(4) при 
Количество допустимых планов такой задачи совпадает с количеством целочисленных решений уравнения

т. е. равно числу сочетаний с повторениями из п элементов по b. Следовательно, при простом переборе число возможных вариантов составит
 .
.
В случае применения метода динамического программирования для вычисления таблицы значений функции  при фиксированном
при фиксированном  необходимо выполнить
необходимо выполнить  операций. Поэтому для заполнения одной таблицы необходимо проделать
операций. Поэтому для заполнения одной таблицы необходимо проделать

операций, из чего получаем, что для вычисления всех функций  ,
,  и
и 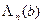 потребуется
потребуется

операций, что при больших п и b существенно меньше, чем в первом случае. Например, если  и
и  , то непосредственный перебор потребует выполнения 324632 операций, а метод динамического программирования - только 2511.
, то непосредственный перебор потребует выполнения 324632 операций, а метод динамического программирования - только 2511.
|
|
|
|
|
|


