 |
Принцип оптимальности Беллмана
|
|
|
|
Подчеркнем, что смысл подхода, реализуемого в динамическом программировании, заключен в замене решения исходной многомерной задачи последовательностью задач меньшей размерности.
Перечислим основные требования к задачам, выполнение которых позволяет применить данный подход:
1. объектом исследования должна служить управляемая система (объект) с заданными допустимыми состояниями и допустимыми управлениями;
2. задача должна позволять интерпретацию как многошаговый процесс, каждый шаг которого состоит из принятия решения о выборе одного из допустимых управлений, приводящих к изменению состояния системы;
3. задача не должна зависеть от количества шагов и быть определенной на каждом из них;
4. состояние системы на каждом шаге должно описываться одинаковым (по составу) набором параметров;
5. последующее состояние, в котором оказывается система после выбора решения на k -м шаге, зависит только от данного решения и исходного состояния к началу k- гошага. Данное свойство является основным с точки зрения идеологии динамического программирования и называется отсутствием последействия.
Рассмотрим вопросы применения модели динамического программирования в обобщенном виде.
Пусть решается задача управления некоторым абстрактным объектом, который может пребывать в различных состояниях. Текущее состояние объекта отождествляется с некоторым набором параметров, обозначаемым в дальнейшем  и именуемый вектором состояния. Предполагается, что задано множество
и именуемый вектором состояния. Предполагается, что задано множество  всех возможных состояний. Для объекта определено также множество допустимых управлений (управляющих воздействий) X, которое, не умаляя общности, можно считать числовым множеством. Управляющие воздействия могут осуществляться в дискретные моменты времени
всех возможных состояний. Для объекта определено также множество допустимых управлений (управляющих воздействий) X, которое, не умаляя общности, можно считать числовым множеством. Управляющие воздействия могут осуществляться в дискретные моменты времени  , причем управленческое решение заключается в выборе одного из управлений
, причем управленческое решение заключается в выборе одного из управлений  . Планом задачи или стратегией управления называется вектор
. Планом задачи или стратегией управления называется вектор  компонентами которого служат управления, выбранные на каждом шаге процесса. Ввиду предполагаемого отсутствия последействия между каждыми двумя последовательными состояниями объекта
компонентами которого служат управления, выбранные на каждом шаге процесса. Ввиду предполагаемого отсутствия последействия между каждыми двумя последовательными состояниями объекта  и
и 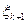 существует известная функциональная зависимость, включающая также выбранное управление:
существует известная функциональная зависимость, включающая также выбранное управление:  ,
, 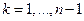 . Тем самым задание начального состояния объекта
. Тем самым задание начального состояния объекта 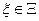 и выбор плана х однозначно определяют траекторию поведения объекта, как это показано на Рис. 5.1.
и выбор плана х однозначно определяют траекторию поведения объекта, как это показано на Рис. 5.1.
|
|
|
Эффективность управления на каждом шаге k зависит от текущего состояния  , выбранного управления
, выбранного управления  и количественно оценивается с помощью функций
и количественно оценивается с помощью функций 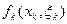 , являющихся слагаемыми аддитивной целевой функции, характеризующей общую эффективность управления объектом. (Отметим, что в определение функции
, являющихся слагаемыми аддитивной целевой функции, характеризующей общую эффективность управления объектом. (Отметим, что в определение функции 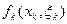 включается область допустимых значений
включается область допустимых значений  , и эта область, как правило, зависит от текущего состояния
, и эта область, как правило, зависит от текущего состояния  ) Оптимальное управление, при заданном начальном состоянии
) Оптимальное управление, при заданном начальном состоянии  сводится к выбору такого оптимального плана
сводится к выбору такого оптимального плана 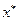 ,при котором достигается максимум суммы значений
,при котором достигается максимум суммы значений  на соответствующей траектории.
на соответствующей траектории.
Основной принцип динамического программирования заключается в том, что на каждом шаге следует стремиться не к изолированной оптимизации функции 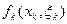 , а выбирать оптимальное управление
, а выбирать оптимальное управление  в предположении об оптимальности всех последующих шагов. Формально указанный принцип реализуется путем отыскания на каждом шаге k условных оптимальных управлений
в предположении об оптимальности всех последующих шагов. Формально указанный принцип реализуется путем отыскания на каждом шаге k условных оптимальных управлений  ,
, 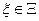 , обеспечивающих наибольшую суммарную эффективность начиная с этого шага, в предположении, что текущим является состояние
, обеспечивающих наибольшую суммарную эффективность начиная с этого шага, в предположении, что текущим является состояние  .
.
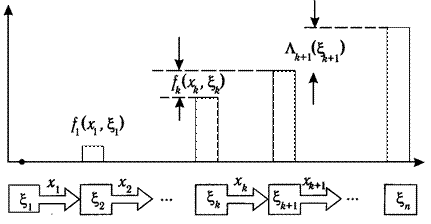
Рис. 5.1
Обозначим  максимальное значение суммы функций
максимальное значение суммы функций  на протяжении шагов от k до п (получаемое при оптимальном управлении на данном отрезке процесса), при условии, что объект в начале шага k находится в состоянии
на протяжении шагов от k до п (получаемое при оптимальном управлении на данном отрезке процесса), при условии, что объект в начале шага k находится в состоянии  . Тогда функции
. Тогда функции  должны удовлетворять рекуррентному соотношению:
должны удовлетворять рекуррентному соотношению:
|
|
|
 (14)
(14)
где  .
.
Соотношение (14) называют основным рекуррентным соотношением динамического программирования. Оно реализует базовый принцип динамического программирования, известный также как принцип оптимальности Беллмана:
Оптимальная стратегия управления должна удовлетворять следующему условию: каково бы ни было начальное состояние  на k-м шаге и выбранное на этом шаге управление
на k-м шаге и выбранное на этом шаге управление  , последующие управления (управленческие решения) должны быть оптимальными по отношению к состоянию
, последующие управления (управленческие решения) должны быть оптимальными по отношению к состоянию  , получающемуся в результате решения, принятого на шаге k.
, получающемуся в результате решения, принятого на шаге k.
Основное соотношение (14) позволяет найти функции  только в сочетании с начальным условием, каковым в нашем случае является равенство
только в сочетании с начальным условием, каковым в нашем случае является равенство
 .
.
Сравнение рекуррентной формулы (14) с аналогичными соотношениями в рассмотренных выше примерах указывает на их внешнее различие. Это различие обусловлено тем, что в задаче распределения ресурсов фиксированным является конечное состояние управляемого процесса. Поэтому принцип Беллмана применяется не к последующим, а к начальным этапам управления, и начальное соотношение имеет вид
 .
.
Важно еще раз подчеркнуть, что сформулированный выше принцип оптимальности применим только для управления объектами, у которых выбор оптимального управления не зависит от предыстории управляемого процесса, т. е. от того, каким путем система пришла в текущее состояние. Именно это обстоятельство позволяет осуществить декомпозицию задачи и сделать возможным ее практическое решение.
В то же время, говоря о динамическом программировании как о методе решения оптимизационных задач, необходимо отметить и его слабые стороны. Так, в предложенной схеме решения задачи (3)-(4) существенным образом используется тот факт, что система ограничений содержит только одно неравенство, и, как следствие, ее состояние задается одним числом - нераспределенным ресурсом  . При наличии нескольких ограничений состояние управляемого объекта на каждом шаге характеризуется уже набором параметров
. При наличии нескольких ограничений состояние управляемого объекта на каждом шаге характеризуется уже набором параметров  , и табулировать значения функций
, и табулировать значения функций  необходимо для многократно большего количества точек. Последнее обстоятельство делает применение метода динамического программирования явно нерациональным или даже просто невозможным.
необходимо для многократно большего количества точек. Последнее обстоятельство делает применение метода динамического программирования явно нерациональным или даже просто невозможным.
|
|
|
|
|
|


