 |
Примеры задач динамического программирования
|
|
|
|
Задача о найме работников. Рассмотрим вопросы применения методов динамического программирования в конкретных экономико-математических моделях.
Отдельно отметим, что данные вычислительные схемы, вообще говоря, достаточно часто используются для решения конкретных задач: задача о ранце, задача о кратчайшем пути, задачи транспортного типа.
Одним из важнейших классов задач, для которых применение динамического программирования оказывается плодотворным, являются задачи последовательного принятия решений. Их особенностью является то, что искомые переменные  должны определяться в строгой временной последовательности и не должны меняться местами. В качестве примера опишем так называемую задачу о найме работников (задачу об использовании рабочей силы).
должны определяться в строгой временной последовательности и не должны меняться местами. В качестве примера опишем так называемую задачу о найме работников (задачу об использовании рабочей силы).
В данной задаче рассматривается некоторый экономический объект (фирма, магазин, завод и т. п.), функционирующий в течение конечного числа периодов, обозначаемых номерами k  . Каждый период k характеризуется нормативной потребностью в определенном количестве однотипных работников
. Каждый период k характеризуется нормативной потребностью в определенном количестве однотипных работников  . Тот же объем работ может быть выполнен другим количеством сотрудников
. Тот же объем работ может быть выполнен другим количеством сотрудников  , что, однако, влечет дополнительные затраты либо за счет нерационального использования рабочей силы, либо ввиду повышения оплаты за интенсивный труд. Размеры этих дополнительных издержек описываются функциями
, что, однако, влечет дополнительные затраты либо за счет нерационального использования рабочей силы, либо ввиду повышения оплаты за интенсивный труд. Размеры этих дополнительных издержек описываются функциями  ,где
,где  - отклонение фактической численности работающих
- отклонение фактической численности работающих  от планово необходимой
от планово необходимой  , причем
, причем  .Управленческое решение на шаге k заключается в выборе величины изменения числа сотрудников
.Управленческое решение на шаге k заключается в выборе величины изменения числа сотрудников  , что однозначно определяет количество работающих в течение следующего периода:
, что однозначно определяет количество работающих в течение следующего периода:  . Затраты по изменению количества работников (найму и увольнению) при переходе от периода k кпериоду
. Затраты по изменению количества работников (найму и увольнению) при переходе от периода k кпериоду 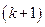 задаются функцией
задаются функцией  , где также
, где также  Тогда суммарные издержки, вызванные принятым на шаге k решением, характеризуются значением функции
Тогда суммарные издержки, вызванные принятым на шаге k решением, характеризуются значением функции
|
|
|
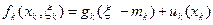 ,
, 
План задачи (стратегия управления) 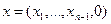 заключается в выборе поэтапных изменений количества работников, а его суммарная эффективность описывается аддитивной функцией
заключается в выборе поэтапных изменений количества работников, а его суммарная эффективность описывается аддитивной функцией
 15)
15)
На основе сформулированной модели ставится задача минимизации целевой функции (издержек) (15). Причём постановка задачи не будет корректной, если не задать начальное условие на количество работников. Существуют две модификации данной задачи, определяемые типом начального условия: в первом случае задается исходное значение на первом этапе  , а во втором - требуемое количество в n -м периоде
, а во втором - требуемое количество в n -м периоде 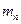 .
.
Рассмотрим первый случай. Поскольку фиксированным является начальное количество работников и, напротив, ничего не известно о том, каким это количество должно быть на последнем этапе, то рассмотрение процесса принятия решений удобнее начать с конца. Оптимальное управление на последнем этапе п по условию равно 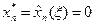 ,поэтому минимальные издержки полностью определяются количеством работников в последнем периоде:
,поэтому минимальные издержки полностью определяются количеством работников в последнем периоде:
 (16)
(16)
Для остальных предшествующих шагов основное рекуррентное соотношение примет вид
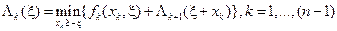 (17)
(17)
где  - минимальные затраты с k -го по n -й периоды, в предположении, что количество работников в k -й период равно
- минимальные затраты с k -го по n -й периоды, в предположении, что количество работников в k -й период равно  . Точки
. Точки  , в которых достигаются минимумы (17), определяют условное оптимальное управление на каждом шаге.
, в которых достигаются минимумы (17), определяют условное оптимальное управление на каждом шаге.
Последовательно определяя  и дойдя до этапа 1, мы сможем найти безусловное оптимальное управление
и дойдя до этапа 1, мы сможем найти безусловное оптимальное управление  из того условия, что на начало первого периода численность работников должна составлять
из того условия, что на начало первого периода численность работников должна составлять  , аименно
, аименно

Остальные компоненты оптимального плана  и состояния
и состояния 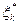 , образующие оптимальную траекторию, последовательно находятся по рекуррентным формулам
, образующие оптимальную траекторию, последовательно находятся по рекуррентным формулам
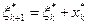 ,
, 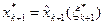 ,
, 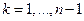
после чего не составляет труда вычислить оптимальное значение целевой функции (15).
|
|
|
Остановимся теперь на втором случае, когда задано финальное состояние управляемого объекта, т. е. желаемое количество работников на последнем периоде 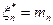 . Очевидно, что в данной ситуации следует поступить с точностью «до наоборот» и рассмотреть процесс принятия решений от начала к концу. Наилучшее условное управление на первом шаге
. Очевидно, что в данной ситуации следует поступить с точностью «до наоборот» и рассмотреть процесс принятия решений от начала к концу. Наилучшее условное управление на первом шаге  будет найдено в процессе вычисления функции
будет найдено в процессе вычисления функции
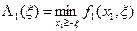 (18)
(18)
где состояние  является возможным количеством работников на начальном шаге. Соответственно, основное рекуррентное соотношение выразит минимальные издержки вплоть до k- гопериода через таковые для предыдущих периодов (с первого по
является возможным количеством работников на начальном шаге. Соответственно, основное рекуррентное соотношение выразит минимальные издержки вплоть до k- гопериода через таковые для предыдущих периодов (с первого по  -й) при условии, что численность работников в k -й период будет равна
-й) при условии, что численность работников в k -й период будет равна  :
:
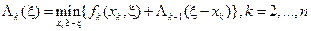 (19)
(19)
Одновременно будут найдены функции  ,
, 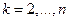 ,определяющие условные оптимальные управления. На последнем периоде, в силу начального условия,
,определяющие условные оптимальные управления. На последнем периоде, в силу начального условия, 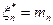 . Отсюда путем последовательного решения рекуррентных уравнений могут быть найдены оптимальные численности работников
. Отсюда путем последовательного решения рекуррентных уравнений могут быть найдены оптимальные численности работников 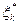 и безусловные оптимальные управления:
и безусловные оптимальные управления:
 ,
,  ,
, 
В заключение, как и в первом случае, подсчитывается минимальная величина издержек.
Обобщая изложенные схемы решения, приходим к выводу:
При использовании алгоритмов динамического программирования, если задано начальное состояние управляемой системы, то задача решается в обратном направлении, а если конечное, то - в прямом. Наконец, если заданы как начальное, так и конечное состояния, то задача существенно усложняется. (В качестве компромисса в этом случае можно отказаться от оптимизации на первом или последнем этапе.)
Продемонстрируем процесс решения задачи о найме работников на конкретном примере:
Для функционирования некоторого предприятия в течение четырех месяцев (нумеруемых от 1 до 4) по нормам требуются следующие количества работников одинаковой квалификации:

причем перед началом первого месяца (в нулевом месяце) фактически имеется  сотрудников. Администрация планирует в конце каждого месяца k (кроме последнего) корректировать число работающих на величину
сотрудников. Администрация планирует в конце каждого месяца k (кроме последнего) корректировать число работающих на величину 
 На прием одного сотрудника необходимо затратить 9 у. е., а на увольнение - 6 у. е. Предполагается, что расходы на содержание избыточного работника составляют 8 у. е., а в случае нехватки персонала приходится нести затраты в размере 12 у. е. за каждое вакантное место.
На прием одного сотрудника необходимо затратить 9 у. е., а на увольнение - 6 у. е. Предполагается, что расходы на содержание избыточного работника составляют 8 у. е., а в случае нехватки персонала приходится нести затраты в размере 12 у. е. за каждое вакантное место.
|
|
|
Требуется найти оптимальные значения приращений численности работающих в конце каждого из первых трех месяцев, при которых суммарные издержки за весь рассматриваемый период будут минимальными.
В начале решения запишем в аналитической форме функции издержек на прием-увольнение сотрудников (и), а также на содержание ненормативного штата (g). С этой целью введем функции
 (20)
(20)
 (21)
(21)
Оценки эффективности управления на каждом шаге имеют вид:
 ;
; 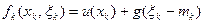 ,
, 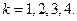
Поскольку в поставленной задаче задано начальное условие  , ее решение начинается с конца, и, следовательно, будут применяться рекуррентные соотношения (17). С технической точки зрения будет удобно на каждом шаге составлять две таблицы значений: функции издержек, получаемых начиная с текущего шага в зависимости от текущего состояния и управления,
, ее решение начинается с конца, и, следовательно, будут применяться рекуррентные соотношения (17). С технической точки зрения будет удобно на каждом шаге составлять две таблицы значений: функции издержек, получаемых начиная с текущего шага в зависимости от текущего состояния и управления,

 (22)
(22)
и функции минимальных издержек в зависимости от текущего состояния
 (23)
(23)
Для сокращения объема табулируемых значений можно воспользоваться свойством выпуклости функции  , вытекающим из выпуклости f и g. Из выпуклости функции
, вытекающим из выпуклости f и g. Из выпуклости функции  следует, что заполнять таблицу ее значений необходимо лишь до тех пор, пока они уменьшаются, т. е. можно остановиться, как только очередное значение оказывается больше предыдущего.
следует, что заполнять таблицу ее значений необходимо лишь до тех пор, пока они уменьшаются, т. е. можно остановиться, как только очередное значение оказывается больше предыдущего.
Итерация 1. Полагаем  . На данном этапе функция состояния
. На данном этапе функция состояния  может быть найдена непосредственно, если учесть, что
может быть найдена непосредственно, если учесть, что 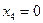 и
и 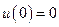 :
:

Таблица значений данной функции и условные оптимальные управления имеют вид

| |||||||

| |||||||

|
Итерация 2. Полагаем 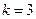 . Предварительно заполним таблицу значений функции
. Предварительно заполним таблицу значений функции  для достаточно большого множества аргументов согласно формуле:
для достаточно большого множества аргументов согласно формуле:
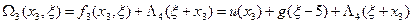

| |||||||||

| -1 | ||||||||

| |||||||||

| |||||||||

|

| |||||||||

| -2 | -1 | -3 | -2 | -1 | -4 | -3 | -2 | |

| |||||||||

| |||||||||

|
|
|
|
Выбирая минимальные по  значения
значения  , составим таблицу
, составим таблицу 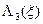 и соответствующие значения условных оптимальных управлений
и соответствующие значения условных оптимальных управлений 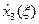 :
:

| ||||||

| ||||||
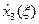
| -1 | -2 | -3 |
Итерация 3. Полагаем  . Так же, как на предыдущей итерации, заполним таблицу значений функции
. Так же, как на предыдущей итерации, заполним таблицу значений функции  согласно формуле:
согласно формуле:


| |||||||||

| -1 | ||||||||

| |||||||||

| |||||||||
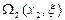
|

| |||||||||

| -1 | -1 | -1 | ||||||

| |||||||||

| |||||||||

|
Выбирая минимальные по  значения
значения  , составим таблицу
, составим таблицу 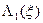 и соответствующие значения условных оптимальных управлений
и соответствующие значения условных оптимальных управлений 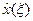 :
:

| ||||||
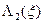
| ||||||

|
Итерация 4. Полагаем  . Аналогично предыдущему, заполним таблицу значений функции
. Аналогично предыдущему, заполним таблицу значений функции  согласно формуле:
согласно формуле:


| |||||||||

| |||||||||

| |||||||||
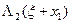
| |||||||||

|

| ||||||

| -1 | |||||

| ||||||
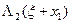
| ||||||

|
Выбирая минимальные по 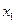 , значения
, значения  , составим таблицу
, составим таблицу 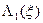 и соответствующие значения условных оптимальных управлений
и соответствующие значения условных оптимальных управлений  :
:

| |||||
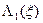
| |||||
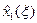
|
Итерация 5. На последней итерации, в связи с наличием начального условия  , достаточно вычислить
, достаточно вычислить
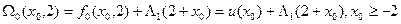
и найти  как точку минимума
как точку минимума  . Простые вычисления показывают, что минимум
. Простые вычисления показывают, что минимум

достигается при  . Следовательно,
. Следовательно,  ,после чего обратным ходом последовательно вычисляются оптимальные управления и оптимальные состояния (оптимальная траектория):
,после чего обратным ходом последовательно вычисляются оптимальные управления и оптимальные состояния (оптимальная траектория):
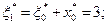
 ;
;

 ;
;

 ;
;
 .
.
Таким образом, результаты расчета свидетельствуют, что при заданной системе расценок в третьем месяце выгоднее не брать 5-го работника, а компенсировать его отсутствие дополнительными выплатами за сверхурочную работу имеющимся сотрудникам.
Динамические задачи управления запасами. Одной из наиболее известных сфер приложения методов динамического программирования является такая область математической экономики, как теория управления запасами. Ее предметом является разработка и исследование математических моделей систем, занимающих промежуточное положение между источниками (производителями) тех или иных ресурсов и их потребителями. При математической формализации процессов управления запасами очень часто приходится использовать скачкообразные, недифференцируемые и кусочно-непрерывные функции. Как правило, это обусловливается необходимостью учета эффектов концентрации, фиксированных затрат и платы за заказ. В связи с этим получаемые задачи с трудом поддаются аналитическому решению классическими методами, однако могут быть успешно решены с помощью аппарата динамического программирования. Рассмотрим достаточно типичную задачу, возникающую в процессе планирования деятельности системы снабжения, - так называемую динамическую задачу управления запасами.
|
|
|
Пусть имеется некоторая система снабжения (склад, оптовая база и т. п.), планирующая свою работу на п периодов. Ее деятельность сводится к обеспечению спроса конечных потребителей на некоторый продукт, для чего она осуществляет заказы производителю данного продукта. Спрос клиентов (конечных потребителей) в данной модели рассматривается как некоторая интегрированная величина, принимающая заданные значения для каждого из периодов, и он должен всегда удовлетворяться (т. е. не допускаются задолженности и отказы). Также предполагается, что заказ, посылаемый производителю, удовлетворяется им полностью, и временем между заказом и его выполнением можно пренебречь (т. е. рассматривается система с мгновенным выполнением заказа). Введем обозначения:
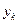 - остаток запаса после
- остаток запаса после  -го периода;
-го периода;
 - заранее известный суммарный спрос в k -м периоде;
- заранее известный суммарный спрос в k -м периоде;
 - заказ (поставка от производителя) в k- мпериоде;
- заказ (поставка от производителя) в k- мпериоде;
 ) - затраты на выполнение заказа объема
) - затраты на выполнение заказа объема  в k- мпериоде;
в k- мпериоде;
 - затраты на хранение запаса объема
- затраты на хранение запаса объема  в k- мпериоде.
в k- мпериоде.
После получения поставки и удовлетворения спроса объем товара, подлежащего хранению в период k, составит  . Учитывая смысл параметра
. Учитывая смысл параметра 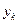 , можно записать соотношение:
, можно записать соотношение:
 . (24)
. (24)
Расходы на получение и хранение товара в период k описываются функцией
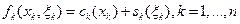 .
.
Планом задачи можно считать вектор  компонентами которого являются последовательные заказы в течение рассматриваемого промежутка времени. Соотношение между запасами (24) в сочетании с некоторым начальным условием связывает состояния системы с выбранным планом и позволяет выразить суммарные расходы за все п периодов функционирования управляемой системы снабжения в форме аддитивной целевой функции:
компонентами которого являются последовательные заказы в течение рассматриваемого промежутка времени. Соотношение между запасами (24) в сочетании с некоторым начальным условием связывает состояния системы с выбранным планом и позволяет выразить суммарные расходы за все п периодов функционирования управляемой системы снабжения в форме аддитивной целевой функции:
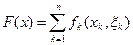 . 25)
. 25)
Естественной в рамках сформулированной модели представляется задача нахождения последовательности оптимальных управлений (заказов)  и связанных с ними оптимальных состояний (запасов)
и связанных с ними оптимальных состояний (запасов) 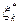 , которые обращают в минимум (25). В качестве начального условия используем требование о сохранении после завершения управления заданного количества товара уп+1, именно
, которые обращают в минимум (25). В качестве начального условия используем требование о сохранении после завершения управления заданного количества товара уп+1, именно
 . (26)
. (26)
При решении поставленной задачи методом динамического программирования в качестве функции состояния управляемой системы  логично взять минимальный объем затрат, возникающих за первые k периодов при условии, что в k- йпериод имеется запас
логично взять минимальный объем затрат, возникающих за первые k периодов при условии, что в k- йпериод имеется запас  . Тогда можно записать основное рекуррентное соотношение
. Тогда можно записать основное рекуррентное соотношение
 ,(27)
,(27)
так как 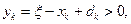 и
и
 . (28)
. (28)
Система рекуррентных соотношений (27)-(28) позволяет найти последовательность функций состояния 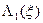 ,
,  ,…,
,…, 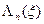 и условных оптимальных управлений
и условных оптимальных управлений 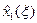 ,
,  ,…,
,…,  . На n -м шаге с помощью начального условия (26) можно определить
. На n -м шаге с помощью начального условия (26) можно определить  . Остальные значения оптимальных управлений
. Остальные значения оптимальных управлений  определяются по формуле:
определяются по формуле:
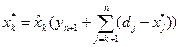 . (29)
. (29)
Особый интерес представляет частный случай задачи (24)- (25), при котором предполагается, что функции затрат на пополнение запаса  являются вогнутыми по
являются вогнутыми по  , a функции затрат на хранение
, a функции затрат на хранение  являются линейными относительно объема хранимого запаса, т. е.
являются линейными относительно объема хранимого запаса, т. е.  . Параллельно заметим, что обе предпосылки являются достаточно реалистичными. Обозначим функцию затрат в течение k- гопериода через
. Параллельно заметим, что обе предпосылки являются достаточно реалистичными. Обозначим функцию затрат в течение k- гопериода через
 (30)
(30)
или, что то же самое,
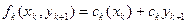 . (31)
. (31)
В силу сделанных предположений все функции затрат  являются вогнутыми (как суммы вогнутой и линейной функций). Данное свойство значительно упрощает процесс решения, так как для поиска минимума вогнутых функций
являются вогнутыми (как суммы вогнутой и линейной функций). Данное свойство значительно упрощает процесс решения, так как для поиска минимума вогнутых функций  достаточно рассмотреть только две крайние точки множества, на котором отыскивается минимум. С учетом введенного обозначения задачу (24)-(25) можно записать в виде:
достаточно рассмотреть только две крайние точки множества, на котором отыскивается минимум. С учетом введенного обозначения задачу (24)-(25) можно записать в виде:
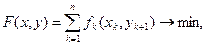 (32)
(32)
при условиях
 . (33)
. (33)
Рассмотрим процедуру решения (32)-(33). Так как ищется минимум суммы вогнутых функций  , то решение будет достигаться на одной из крайних точек множества, определяемого условиями (33). Общее число переменных
, то решение будет достигаться на одной из крайних точек множества, определяемого условиями (33). Общее число переменных  и
и 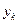 в системе (33) равно
в системе (33) равно  . Однако, учитывая то, что в ней только п уравнений, в оптимальном плане будет не более п ненулевых компонент, причем для каждого периода k значения
. Однако, учитывая то, что в ней только п уравнений, в оптимальном плане будет не более п ненулевых компонент, причем для каждого периода k значения  и
и 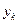 не могут равняться нулю одновременно (в силу необходимости удовлетворения спроса либо за счет заказа, либо за счет запаса). Формально это утверждение можно представить в виде условия дополняющей нежесткости:
не могут равняться нулю одновременно (в силу необходимости удовлетворения спроса либо за счет заказа, либо за счет запаса). Формально это утверждение можно представить в виде условия дополняющей нежесткости:
 ,(34)
,(34)
где
 (35)
(35)
С точки зрения содержательной интерпретации условия (34)-(35) означают, что при оптимальном управлении заказ поставщику на новую партию не должен поступать, если в начале периода имеется ненулевой запас, или размер заказа должен равняться величине спроса за целое число периодов. Отсюда следует, что запас на конец последнего периода должен равняться нулю:  Последнее позволяет решать задачу в прямом направлении, применяя рекуррентное соотношение
Последнее позволяет решать задачу в прямом направлении, применяя рекуррентное соотношение
 , (36)
, (36)
где  .
.
Учитывая (34)-(35) и вогнутость  заключаем, что минимум (36) достигается в одной из крайних точек
заключаем, что минимум (36) достигается в одной из крайних точек  или
или  , поэтому
, поэтому
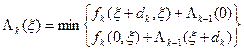 , (37)
, (37)
тогда для предыдущего периода функция состояния может быть выражена в виде
 (38)
(38)
Следовательно, в общем виде получаем модифицированную форму для рекуррентного соотношения
 . (39)
. (39)
При дальнейших конкретизирующих предположениях о виде функций  можно получить еще более компактные формы для рекуррентных соотношений.
можно получить еще более компактные формы для рекуррентных соотношений.
|
|
|


