 |
Декартовы координаты и векторы в пространстве.
|
|
|
|
Вопросы самоконтроля
1. Дать определение определенного и неопределенного интегралов.
2. Что вычисляют с помощью формулы Ньютона-Лейбница?
3. Сформулировать физический и геометрический смысл определенного интеграла.
4. Какую фигуру называют криволинейной трапецией.
5. Как вычислить площадь криволинейной трапеции расположенной выше оси абсцисс и ниже оси абсцисс.
Раздел №6
Декартовы координаты и векторы в пространстве.
Аксиомы стереометрии. Параллельность и перпендикулярность в пространстве.
Цель задания: углубить знания по теме, закрепить практические навыки и способы решениязадач по теме «Параллельность и перпендикулярность в пространстве».
Задание для самоподготовки:
1. Подготовить опорные конспекты по формулам планиметрии.
2. Решить задания №1 и №2 с целью повышения оценки контроля данного модуля.
Задания №1
Номер n соответствует номеру по списку классного журнала.
Вычислить площадь плоскости, заданной уравнением в отрезках
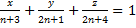. В решении задания использовать формулы вычисления расстояния между двумя точками и угла между векторами.
Задание №2
З а д а ч а 1. Отрезка АВ не пересекает плоскость α, точка А и В удалены от плоскости α на 7 см и 11 см. Найти расстояние от середины отрезка АВ до плоскости α.
З а д а ч а 2. Из точки А к плоскости α проведены наклонные АВ и АС, длины которых равны 15 см и 20 см соответственно. Найти расстояние от точки А до плоскости α, если проекции наклонных на эту плоскость относятся как 9: 16.
З а д а ч а 3. Из точки М к плоскости α проведены наклонные МN и МК, длины которых относятся как 25: 26. Найти расстояние от точки М до плоскости α, если длины проекций наклонных на эту плоскость равны 7 см и 10 см.
|
|
|
З а д а ч а 4. Из точки М к плоскости α проведены наклонные МВ и МС, образующие с плоскостью углы 30º. Найти расстояние от точки М до плоскости α, если 
ВМС = 90º, а длина отрезка ВС = 8 см.
Вопросы самоконтроля
1. Формула расстояния между двумя точками.
2. Скалярное произведение векторов.
3. Формула вычисления угла между векторами.
4. Аксиомы стереометрии.
5. Параллельность плоскостей.
6. Перпендикулярность плоскостей.
7. Теорема о трех перпендикулярах.
8. Формула площади ортогональной проекции многоугольника.
Раздел №7
Многогранники и тела вращения
Цель задания: углубить знания по теме, закрепить практические навыки и способы решениязадач по теме «Многогранники и тела вращения», развитие творческих и научно-исследовательских способностей.
Задание для самоподготовки:
1. Подготовить доклады в виде презентации «Многогранники в быту, природе и повседневной жизни», «Интересные факты о пирамиде».
2. Изготовить геометрическую модель многогранника и составить задачу на нахождение его различных элементов, площади боковой и полной поверхности, объема.
3. Решить задачи, выполнив чертеж на чистом листе А4.
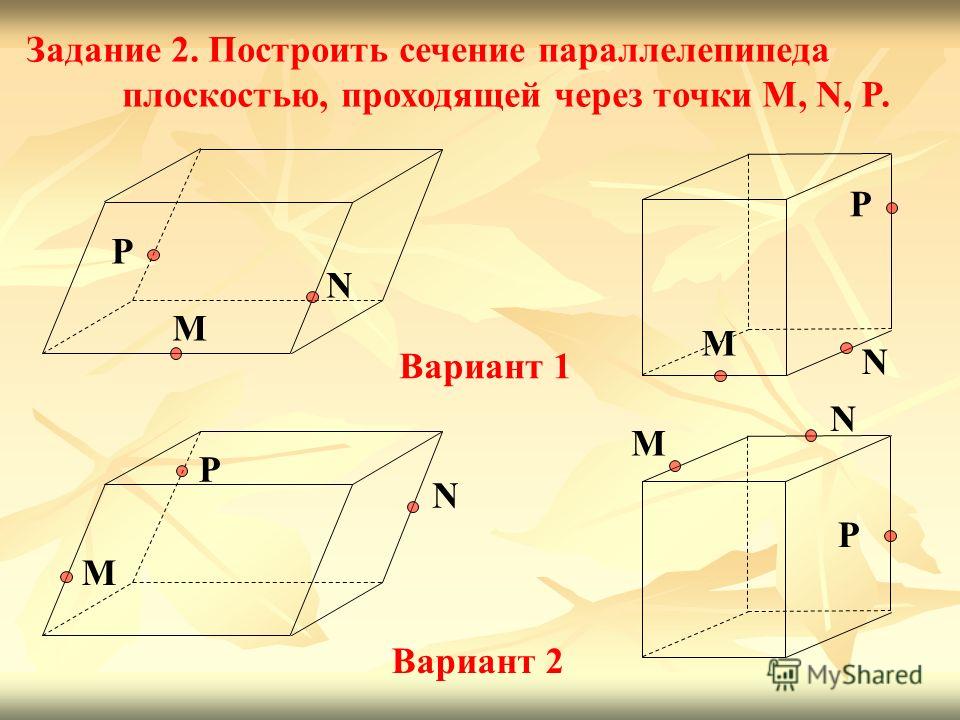
Построить сечение параллелепипеда плоскостью, проходящей через точки M, N, P.
Критерии оценивания знаний
5 (ОТЛИЧНО)
Студент владеет всем программным материалом, последовательно, обосновано, без ошибок устно и письменно излагает теоретический материал. Правильно и аккуратно оформляет письменные и графические задания, уверенно и целесообразно использует знания при решении практических задач.
4 (ХОРОШО)
Студент знает и понимает весь программный материал, обоснованно использует знания с допущением незначительных ошибок. Правильно и опрятно оформляет письменную работу. Применяет теоретические знания для решения практических задач, допуская незначительные неточности.
|
|
|
3 (УДОВЛЕТВОРИТЕЛЬНО)
Студент знает и понимает теоретический материал в объеме, который позволяет выполнение последующей работы, неполно, упрощенно излагает теоретический материал с ошибками и неточностями. Правильно оформляет письменные и графические работы. С осложнениями применяет теоретически знания к решению практических заданий.
2 (НЕУДОВЛЕТВОРИТЕЛЬНО)
Студент слабо понимает большую часть теоретического материала, излагает его с грубыми ошибками, неаккуратно оформляет письменные и графические работы, не может применить теоретические знания или допускает значительное количество ошибок при решении практических задач.
| УТВЕРЖДАЮ |
| Заместитель директора |
| по учебной работе |
| _________В. В. Ширяева |
| «___»____________2019 г. |
|
|
|
