 |
По дисциплине ОУД. 03 математика
|
|
|
|
ВОПРОСЫ К ЭКЗАМЕНУ
ПО ДИСЦИПЛИНЕ ОУД. 03 МАТЕМАТИКА
1. Определение предела функции в точке.
2. Методы решений пределов функции с неопределенностью 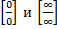
3. Определение производной функции.
4. Правила дифференцирования.
5. Логарифмическое дифференцирование.
6. Таблица производных.
7. Схема исследования функции с помощью производной.
8. Определение первообразной функции.
9. Определение неопределенного интеграла.
10. Методы интегрирования. Таблица интегралов.
11. Определенный интеграл. Формула Ньютона—Лейбница.
12. Правила вычисления площади криволинейной трапеции.
13. Прямоугольная система координат в пространстве.
14. Определение вектора. Векторы в пространстве.
15. Формула расстояния между точками в пространстве, угол между векторами в пространстве.
16. Формула деления отрезка в данном отношении.
17. Определение двугранного угла.
18. Признак параллельности плоскостей.
19. Теорема о трех перпендикулярах.
20. Формула площади ортогональной проекции многоугольника.
21. Определение многогранника. Виды многогранников.
22. Определение призмы. Виды призм. Формула объема, полной и боковой поверхности призмы.
23. Определение пирамиды. Виды пирамид. Формула объема, полной и боковой поверхности пирамиды.
24. Усеченный конус и пирамида. Формула объема, полной и боковой поверхности усеченного конуса и пирамиды.
25. Тела вращения. Формула вычисления объема тела вращения.
26. Конус. Сечения конуса плоскостью. Формула объема, полной и боковой поверхности конуса.
27. Цилиндр. Сечения цилиндра плоскостью. Формула объема, полной и боковой поверхности цилиндра.
28. Шар. Сфера. Формула объема шара и площади сферы. Вывести формулу объема шара.
|
|
|
| Рассмотрено и утверждено на заседании цикловой комиссии общеобразовательных, ЕН и ОГСЭ дисциплин Протокол от «___»___________2019 г., №__ Председатель цикловой комиссии ______________В. В. Скрипников |
Электронные ресурсы
1. http: //mathprofi. ru – ресурс содержит полезные учебные материалы, изложенные в доступной форме, подробные разъяснения практических заданий.
2. http: //mathportal. net – сайт создан для помощи студентам, желающим самостоятельно изучать математику, и помощи преподавателям в подборке материалов к занятиям и контрольным работам;
3. http: //free. megacampus. ru – открытая библиотека электронных учебных курсов.
Литература
1. Алимов Ш. А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни). 10—11 классы. — М.: Просвещение, 2015.
2. Шкиль Н. И., Слепкань З. И, Дубинчук Е. С. Алгебра и начала анализа: учебник для 10 класса. – К.: Зодиак – ЭКО, 2006. –267с.
3. Богомолов Н. В., Самойленко П. И. «Математика», М: Дрофа, 2002 г.
4. Башмаков М. И. «Математика», учебник для 10 кл. (базовый уровень). М: Издательский центр «Академия»», 2008 г.
5. Башмаков М. И. «Математика», учебник для 11 кл. (базовый уровень). М: Издательский центр «Академия»», 2010 г.
6. Башмаков М. И. Математика: учебник для учреждений нач. и сред. проф. образования. – М.: Издательский центр «Академия», 2012.
7. Яковлев Г. Н. «Алгебра и начала анализа», часть 1. М: Наука, 1988 г.
8. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала анализа. Геометрия (базовый и углубленный уровни). 10—11классы. — М.: Просвещение, 2014.
9. Колягин Ю. М. и др. «Алгебра и начала математического анализа», учебник для 10 кл. общеобразовательных учреждений. М: Просвещение, 2008 г.
10. Колягин Ю. М. и др. «Алгебра и начала математического анализа», учебник для 11 кл. общеобразовательных учреждений. М: Просвещение, 2009г.
|
|
|


