 |
● Классическая формула сложения вероятностей
|
|
|
|
● Классическая формула сложения вероятностей
1. Независимо друг от друга 5 человек садятся в поезд, содержащий 13 вагонов. Найдите вероятность того, что все они поедут в разных вагонах.
2. В партии из 13 деталей имеется 8 стандартных. Наудачу отобраны 7 деталей. Найдите вероятность того, что среди отобранных деталей ровно 5 стандартных.
3. В киоске продается 9 лотерейных билетов, из которых число выигрышных составляет 3 штуки. Студент купил 4 билета. Какова вероятность того, что число выигрышных среди них будет не меньше 2, но не больше 3?
| Всего | Выигрыш | Проигрыш | |
| Было | 9 | 3 | 6 |
| Отобрано 1 | 4 | 2 | 2 |
| Отобрано 2 | 4 | 3 | 1 |
4. В группе учатся 13 юношей и 9 девушек. Для дежурства случайным образом отобраны три студента. Найдите вероятность того, что все дежурные окажутся юношами.
5. Имеется 25 экзаменационных билетов, на каждом из которых напечатано условие некоторой задачи. В 15 билетах задачи по статистике, а в остальных 10 билетах задачи по теории вероятностей. Трое студентов выбирают наудачу по одному билету. Найдите вероятность того, что хотя бы одному из них не достанется задачи по теории вероятностей.
6. В ящике 3 белых и 4 черных шаров. Найдите вероятность того, что из двух вынутых наудачу шаров один белый, а другой черный. Вынутый шар в урну не возвращается.
7. В ящике 12 шаров, из них 3 белых, а остальные – черные. Из ящика наугад берут 5 шаров. Какова вероятность, что среди выбранных есть хотя бы один белый шар?
● Геометрические вероятности
8. В квадрат со стороной 15м случайным образом вбрасывается точка. Найдите вероятность того, что эта точка окажется в правой верхней четверти квадрата или не далее, чем на 2м от центра квадрата.
|
|
|
9. На отрезок 
длины 240 наудачу поставлена точка 
. Найдите вероятность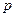 
того, что меньший из отрезков 
и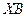 
имеет длину большую, чем 48.
10. На отрезок длины 120 наудачу поставлена точка . Найдите вероятность 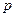того, что меньший из отрезков и 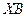имеет длину меньшую, чем 30.
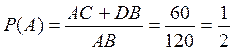
11. На плоскости начерчены две концентрические окружности, радиусы которых 20 и 100 соответственно. Найдите вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями.
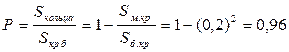
12. Внутрь круга радиуса 50 наудачу брошена точка. Какова вероятность того, что точка окажется внутри вписанного в круг квадрата? правильного треугольника? правильного шестиугольника?
13. Двое договорились о встрече между 6 и 7 часами утра, причем договорились ждать друг друга не более 5 минут. Считая, что момент прихода на встречу выбирается каждым наудачу в пределах указанного часа, найти вероятность того, что встреча состоится.
14. В шар радиуса 150 наудачу бросаются 2 точки. Найдите вероятность того, что расстояние от центра шара до ближайшей точки будет не меньше 120.
15. В круг радиуса 150 наудачу бросаются 4 точки. Найдите вероятность того, что расстояние от центра круга до ближайшей точки будет не меньше 75.
16. В шар радиуса 100 наудачу бросаются 4 точки. Найдите вероятность того, что расстояние от центра шара до самой удаленной точки будет не больше 50.
● Правила сложения и умножения вероятностей
17. Пусть 
– вероятности событий. Найдите наименьшую возможную вероятность события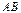 
.
18. Вероятность события 
, 
, 
Найдите наименьшую возможную вероятность события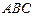 
.
19. В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны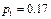 
, 
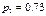и 
. Найдите вероятность того, что тока в цепи не будет.
|
|
|
А-событие, сост. в том, что тока нет
-событие, сост. в том, что ток есть
=В1, В2, В3
Вi-событие, сост. в том, что прибор исправен
20. Вероятность хотя бы одного попадания в мишень при 9 выстрелах равна 0. 81. Найдите вероятность 
попадания при одном выстреле.
А-событие, сост. в том, что при 9 выстрелах в мишень попадут 1 раз
P(A)=0. 81
А с чертой – событие, сост. в том, что в мишень не попали ни разу
Вероятность непопадания при 1 выстреле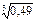 
След, вероятность попадания 1 выстрела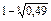 
21. Пассажир подходит к остановке автобусов двух маршрутов. Интервал движения автобусов 1-го маршрута составляет 
мин., а 2-го маршрута – 
мин. Найдите вероятность того, что пассажир уедет с остановки не позднее, чем через 
мин., считая, что его устроит автобус как 1-го, так и 2-го маршрутов.
А-событие, сост. В том, что уедет не позднее, чем через 6 мин
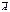-опоздает
В-1 авт. Прибудет позднее 6 мин
С – 2 авт. Прибудет позднее 6 мин
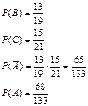
22. В ящике 8 белых и 13 черных шаров. Два игрока поочередно извлекают по шару, каждый раз возвращая его обратно. Выигрывает тот, кто первым вытащит белый шар. Какова вероятность выигрыша для начинающего игру?
А-событие, сост. в том, что достали белый шар
23. Вероятность того, что при одном измерении некоторой физической величины допущена ошибка, равна 0. 05. Найдите наименьшее число 
измерений, которые необходимо произвести, чтобы с вероятностью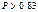 
можно было ожидать, что хотя бы один результат измерений окажется неверным.
А-хотя бы 1 раз результат окажется неверным
А с чертой- все верны
А с чертой= В1, …Вn
Bi- где i результат верен
|
|
|
