 |
Вывод уравнений для импульсного относительного движения двух КА.
|
|
|
|
ПРАКТИЧЕСКАЯ ЧАСТЬ.
Вывод уравнений, решением дифференциальных уравнений движения, применительно к пассивному относительному движению двух КА.
Возьмем уравнение:
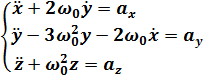

Оно выражает относительное движение двух КА по произвольной орбите. Причем один из аппаратов пассивно движется по опорной невозмущенной кеплеровой орбите, а второй движется активно (маневрируя) по орбите, которая может отличаться от опорной как за счет начального рассогласования орбит, так и за счет действия возмущающего ускорения.
Решение этого уравнения подробно описано ранее. Получаем:  (3.1)
(3.1)
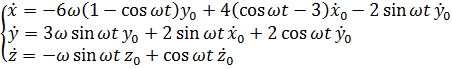 (3.2)
(3.2)
Данные системы уравнений можно решить и численным методом, однако это потребует больших вычислительных мощностей, поэтому мы решим это иным способом.
Введем подстановку:
 (3.3)
(3.3)


Действуя тем же методом, находим:
 (3.4)
(3.4)
Выполним замену в выражение (1):
 (3.5)
(3.5)
Решив дифференциальные уравнения (3.4), получаем:
 (3.7)
(3.7)
Решив систему уравнений (3.3) найдем x, y, z,  ,
,  от
от 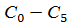 :
:
 (3.8)
(3.8)
Вывод уравнений для импульсного относительного движения двух КА.
До этого момента, мы рассматривали случай относительного движения без ускорения:  .
.
Однако, космические аппараты движутся не только пассивно, но и с приложением ускорения – именно таким образом мы изменяем орбиту и траекторию движения в зависимости от того, как нам это необходимо.
Для начала рассмотрим уравнение движения, когда в некий момент времени пассивного движения дается мгновенный импульс.
Импульсом мы считаем поданное ускорение  ,
,  ) за бесконечно малый промежуток времени. В данном случае импульс можно считать дельта-функцией.
) за бесконечно малый промежуток времени. В данном случае импульс можно считать дельта-функцией.
Обозначим момент начала движения за  , момент окончания движения
, момент окончания движения 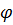 , а момент, когда дан импульс за
, а момент, когда дан импульс за 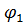 :
:
|
|
|

|
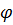
|

|

|

|

|
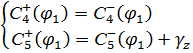
Коэффициент с индексом «+», это коэффициент после импульса, а с индексом «-», до импульса.
Соответственно, с момента времени  , до
, до 
 , а с момента времени
, а с момента времени  , до
, до 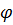
 .
.
3.2.1. Вывод уравнения импульсного относительного движения из общего уравнения движения  , двумя методами.
, двумя методами.
Рассмотрим, для начала, для наиболее простое уравнение относительного движения из системы (6.16):
 ,
, 
Его решение в общем виде ( =0) имеет вид:
=0) имеет вид:
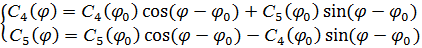 (3.9)
(3.9)
Мы вычислили это в предыдущем пункте.
Теперь решим это же уравнение, но пойдем дальше, и уже не будем считать, что ускорение равно нулю, а решим уравнение применительно к импульсу. Для проверки результатов, а так же для выявления наиболее быстрого способа решения для использования его в последующем, решим этот случай двумя способами.
Решение  , для импульсного движения, методом вариации произвольных постоянных Лагранжа.
, для импульсного движения, методом вариации произвольных постоянных Лагранжа.
Сущность метода состоит в том, чтобы найти сначала решение уравнений в общем виде, для однородного уравнения. Вид решений неоднородного уравнения останется прежним, только постоянные перестанут быть константами, а станут функциями по времени. Таким образом, остается только найти эти функции.
Теперь перейдем к решению случая, когда  (неоднородное уравнение), не забывая, что константы станут функциями по времени:
(неоднородное уравнение), не забывая, что константы станут функциями по времени:

Понизим степень уравнений:
 , уравнения примут вид:
, уравнения примут вид:
 (3.10)
(3.10)
Подставим (3.10) в 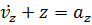 :
:


Теперь подставим (3.10) в  :
:


После сокращений остается:

Теперь выразим константы:
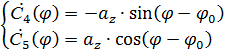
Проинтегрировав получим следующие функции:
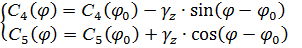
Такое решение интеграла мы получаем в связи с тем, что интегрируем дельта-функцию по бесконечно малому отрезку времени.
Если мы будем считать тем же способом для n импульсов, то получим следующий результат:

Таким образом, мы видим, что для расчета нескольких импульсов этим способом решение меняется от одноимпульсного на последнем шаге.
|
|
|
Так как координаты для конечного момента относительного движения 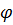 , часто принимают за ноль (оба аппарата оказались в одной точке), то для удобства, выразим
, часто принимают за ноль (оба аппарата оказались в одной точке), то для удобства, выразим  из выражения (3.9):
из выражения (3.9):


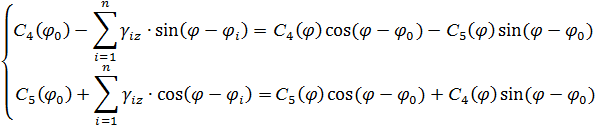
Объединим эти уравнения и произведем обратную замену переменных. Для этого мы помножим первое уравнение на  , а второе на
, а второе на 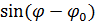 и сложим их:
и сложим их:





Таким образом, мы получили общую формулу, благодаря которой можем определить конечные параметры при заданных начальных условиях и данных об импульсах.
|
|
|


