 |
А) для случая движения с постоянной скоростью и гашением ее на последнем участке.
|
|
|
|
Тогда:
| t0 |
| x |
| y |
| Vx1 |
| tk |
| Vx2 |
| ax |
| ay |
Vx1 – импульс начинающий движение; Vx2 –импульс заканчивающий движение; ay – ускорение прикладываемое по оси Y по всему пути движения для стабилизации орбиты на заданной нами (нелинейное); ax – ускорение прикладываемое по оси Y по всему пути движения для стабилизации орбиты на заданной нами;
Найдем интеграл от нелинейного ускорения 
:
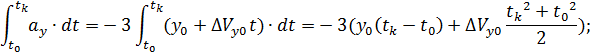
Тогда, полная скорость за маневр:
б) для случая постепенно уменьшающейся скорости до нуля на последнем участке.
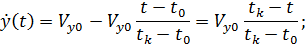
Найдем интегралы от ускорений 
:
Тогда, полная скорость за маневр:
Таким образом, мы рассмотрели два простых реальных примера, в которых применили найденные нами формулы относительного движения, как импульсные, так и с протяженной тягой. При построении этой модели в разработанной ранее программе, все вычисления сошлись.
4. Разработка ПО на языке С++ позволяющего оптимизировать процесс вычисления импульса для перехода с различных орбит на заданную.
В задачах космического движения одной из важнейших является задача об относительном движении. В тематике же относительного движения чаще других встречаются задачи об относительном движении двух космических аппаратов.
Относительное движение двух КА можно разделить на две задачи:
- Задача перехвата;
- Задача сближения.
Задача перехвата – заключается в формировании такой траектории относительного движения, что в заданный момент времени координаты обоих КА совпадают. При этом, ограничений на относительные скорости не накладывается.
Задача сближения – заключается в формировании такой траектории относительного движения, что в заданный момент времени координаты обоих КА совпадают, а также относительная скорость равна нулю.
|
|
|
Для двухимпульсной траектории (гоумановский переход):
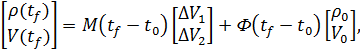(4.1)
Где
При этом, матрица 
задается следующим образом:
Первым импульсом формируется траектория перехвата, а вторым импульсом в точке перехвата выравниваем относительную скорость.
Чтобы найти импульс, необходимо воспользоваться следующей формулой, полученной из (4.1):
(4.2)
Если число импульсов в задаче сближения больше двух, то может быть сформулирована оптимизационная задача. Эта задача является нелинейной т.к. присутствует модуль.
В рамках проекта, я разработал программу позволяющую вычислить импульс по формуле (4.2) по введенным начальным условиям.
Для работы программы необходимо ввести начальный вектор (rv(0)), конечный вектор (rv(f)), начальное время (t(0)), конечное время (t(f)), и омегу. После чего нажать кнопку «Вычислить импульс».
Внешний вид программы после запуска:
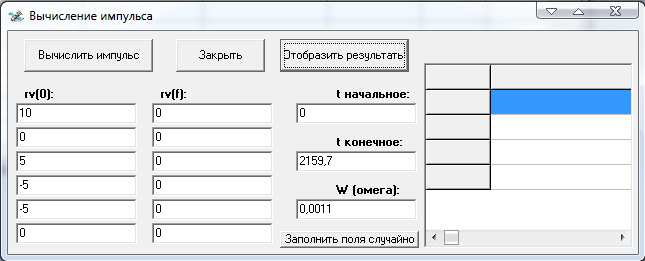
В случае если вычисление невозможно, программы выдаст ошибку. Для продолжения вычислений необходимо перезапустить ее и ввести данные без ошибок.
Кроме того, для тестирования программы встроена кнопка «Заполнить поля случайно», при нажатии на которую можно мгновенно заполнить все поля.
Результат вычислений, шестимерный вектор, отобразится в поле справа в главном окне программы. Для отображения промежуточных результатов вычисления, как то, 
, 
, rvk (
), необходимо нажать на кнопку «Отобразить результаты». В случае, если пользователь нажмет на кнопку «Отобразить результаты» раньше, чем на кнопку «Вычислить импульс», все поля будут заполнены нулями. Кроме того, в этой таблице (второе окно «Таблица результатов») отображаются начальные условия для удобства их проверки.
После выполнения программы в папке ее хранения автоматически создается файл «Uslovie.txt», где сохраняются все содержимое окна «Таблица результатов». Благодаря этому пользователь может легко импортировать полученные данные в другие программы (Microsoft Office Word, Microsoft Origin и другие), а также иметь доступ к вычисленным данным и после закрытия программы. Обратите внимание, для экономии места на жестком диске пользователя, сохраняются только результаты последнего нажатия на кнопку «Вычислить импульс».
|
|
|
|
|
|
