 |
Вывод уравнений для относительного движения, с протяженной тягой, двух КА.
|
|
|
|
В пунктах 3.1 и 3.2 мы рассматривали относительное движение двух КА на пассивном участке и при мгновенно выданных импульсах соответственно. Однако движение КА не ограничивается пассивным, а также импульс в реальных условиях далек от дельта функции (в реальных условиях импульс прикладывается некоторое конечное время). Соответственно нам необходимо рассмотреть самый важный аспект – относительное движение с протяженной тягой.
Под «протяженной тягой», в данном случае, следует понимать ускорение прикладываемое к объекту в течении некоторого конечного промежутка времени.
И так, в качестве основы для вычислений, опять возьмем найденные нами общие уравнения относительного движения двух КА (2.16):
Здесь можно явно различить две независимые системы:
и 
3.3.1. Вывод уравнений для x 
и y .
Для начала выведем уравнения для первой системы.
Решение первой системы мы находили ранее:
или, после подстановок:
(3.12)
Для последующих вычислений мы будем пользоваться системой (3.12).
Найдем 
из уравнения (3.12):
Общий вид уравнений нам известен – он останется таким же как и в системе уравнений (3.12). Однако нам неизвестны коэффициенты 
. В их нахождении и состоит наша задача.
Мы имеем систему дифференциальных уравнений второго порядка. Чтобы решить ее необходимо понизить степень уравнений и получить столько дифференциальных уравнений первого порядка, сколько неизвестных у нас получится.
Переобозначим переменные:
(3.14)
Теперь запишем четыре новых уравнения для четырех неизвестных, исходя из подстановки (3.14):
Как мы нашли в предыдущих главах:
;
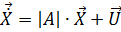; (3.15)
Запишем уже известные нам элементы этого уравнения:
|
|
|
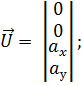
Соответственно, нам необходимо найти только одну недостающую матрицу – матрицу 
, ее мы построим из выражений (3.12) и (3.13) как коэффициенты при 
в каждом из уравнений:
Продифференцировав (3.15) получим:
;
Соответственно, поставим в полученное выражение известные нам матрицы и перейдем обратно, к системам уравнений:
Теперь мы можем выразить 
.
Таким образом не выраженной осталось только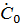 
. Сделаем это:
Мы получили производные необходимых нам функций:
Чтобы найти функции , возьмем интеграл, от их производных. При этом коэффициентом интегрирования будет сама функция для момента времени 
:
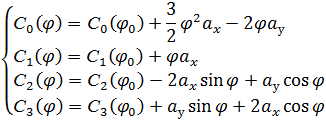
Таким образом, мы нашли коэффициенты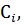 
общий вид уравнений относительного движения с протяженной тягой, нам известен – он останется таким же как и в системе уравнений (3.12). Теперь осталось только подставить коэффициенты в уравнения.
;
;
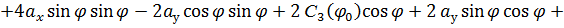
3.3.2. Вывод уравнений для z .
Теперь выведем уравнение протяженного движения для:
(3.16)
Решением данного уравнения будет являться следующая система:
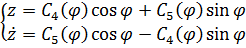(3.17)
Чтобы понизить степень дифференциального уравнения введем подстановку:
Тогда уравнение примет вид
(3.18)
(3.19)
Подставим уравнения (3.18) и (3.17(2)) в уравнение (3.16):
Вычтем уравнение (3.19) из (3.17(1)):
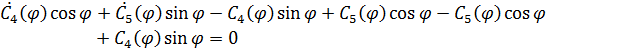
После сокращений получаем:
Выразим 
:
Проинтегрируем эти функции. При этом коэффициентом интегрирования будет сама функция для момента времени :
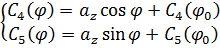
Подставим полученный результат в (3.17(1)):
.
Итого. Запишем все полученные уравнения относительного движения с протяженным приложением ускорения, которые мы нашли:
Применение полученных формул относительного движения.
Движение вдоль оси х без изменения положения по осям y и z.
Это означает, что начальные условия нашего движения:
x0 = X0 , 
, t0 = 0,
y0 = z0 =0, 
, 
Из уравнения (3.0), подставив начальные условия находим:
|
|
|
Рассмотрим два случая:
|
|
|
