 |
Проверка погрешности полученной математической модели.
|
|
|
|
В заключение сопоставим результаты расчета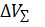 
по линеаризованной теории с результатами расчетов по методике Райдера для случая перелетов между некомпланарными круговыми орбитами. По теории Райдера при малых 
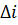и 
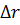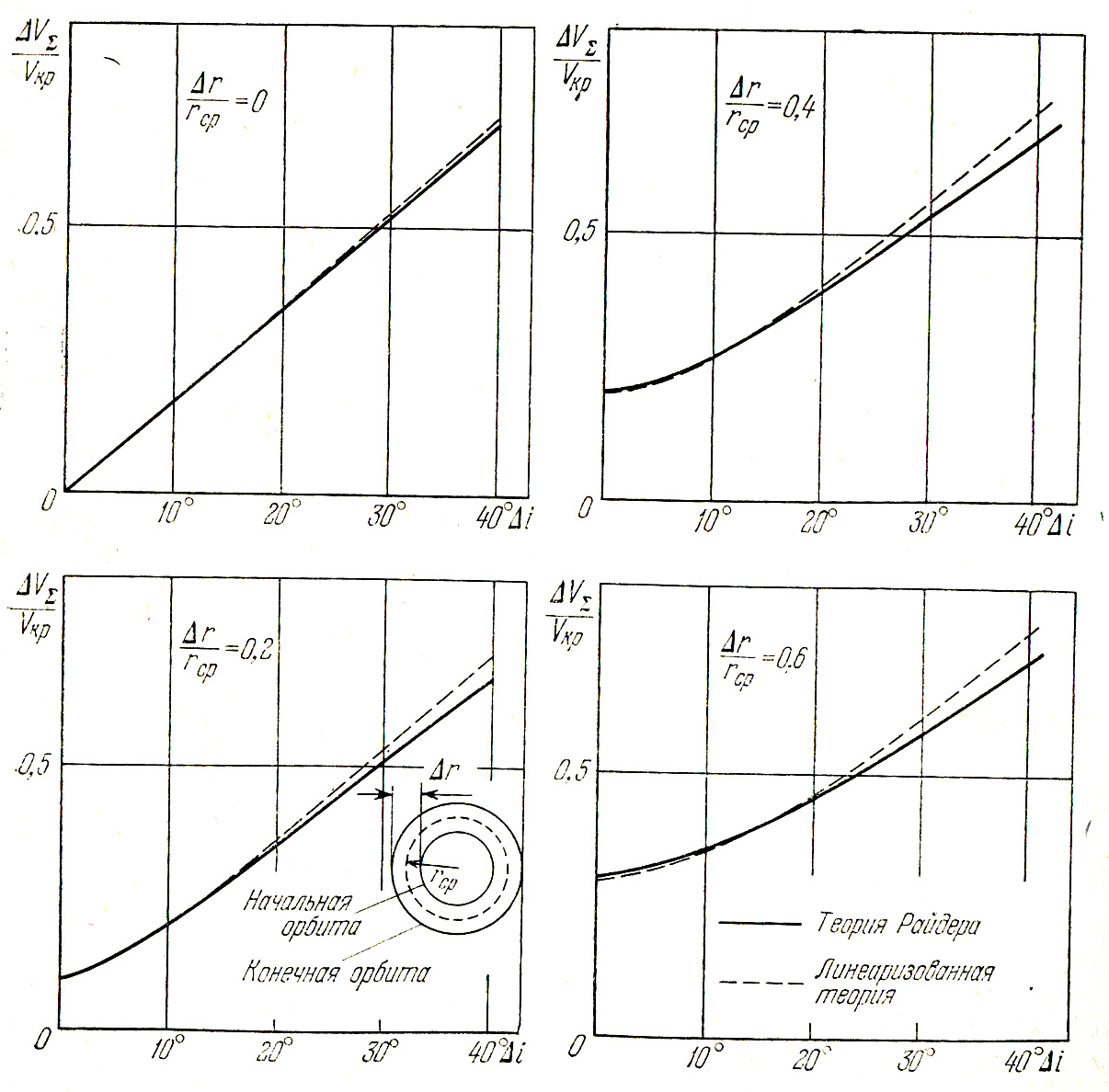
оптимальный перелет осуществляется с помощью двух пространственных импульсов, прикладываемых в узловых точках. Это совпадает с выводами линеаризованной теории. Результаты расчетов 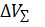по линеаризованной теории и по методике Райдера представлены на рисунке 5.1. При определении 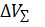- безразмерной характеристической скорости – по методике Райдера она относилась к круговой скорости, определенной для 
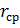, равно полусумме радиусов начальной и конечной орбит.
Данные вычислений по методике Райдера взяты из вычислений Ильина [2]. Видно, что при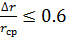 
и 
погрешность не превышает 3%.
ЗАКЛЮЧЕНИЕ.
Решение задачи о движении ЛА является одной из важнейших проблем, на которых базируется проектирование в целом, так как движение — это тот процесс, в результате которого ЛА выполняет свое назначение. Движение должно быть организовано рационально, с учетом ряда ограничивающих факторов и условий, стесняющих наш выбор. В некоторых случаях имеется единственная траектория, решающая поставленную перед ЛА задачу, - ее и надо найти; в других случаях из множества возможных решений надо выбрать одно, являющееся в каком-то смысле наилучшим. От того, насколько удачно решена задача о движении, зависят важнейшие характеристики ЛА (начальная масса, тяга двигательной установки, масса полезного груза на орбите и т.д.) и задачи полета (надежность достижения заданной цели, эффективность функционирования ЛА или системы ЛА, дальность полета, точность выведения и т.д.).
|
|
|
В данной работе мы решили лишь одну из многих проблем, однако не менее важную – проблему расчета относительного движения двух космических аппаратов, один из которых движется пассивно по опорной орбите, а другой активно.
Была изучена теоретическая база, выведены и решены все необходимые уравнения движения в рамках поставленной задачи.
Это уравнения пассивного относительного движения, уравнения пассивного движения с n количеством импульсов, а также, движение с протяженной тягой. При этом, последний тип движения является наиболее применимым и необходимым при расчете траекторий движения.
Так же, была модифицирована, разработанная нами ранее, программа позволяющая оптимизировать процесс вычислений, а так же выдающая файл с таблицей благодаря которой наглядно видно, как изменяются все величины на протяжении времени. Кроме того, благодаря тому, что не приходиться выполнять сотни однообразных вычислений, были построены весьма точные траектории движения активного космического аппарата, относительно пассивного.
Мы рассмотрели несколько реальных примера маневров, благодаря чему проверили правильность и актуальность своих расчетов и выводов, рассчитав сначала в ручную по найденным нами формулам, после чего сравнив с компьютерной математической моделью. Результаты оказались верны.
СПИСОК ЛИТЕРАТУРЫ.
1). Ю.А.Ермилов, Е.Е.Иванова – «Управление сближением космических аппаратов», Москва 1979г.
2). В.А.Ильин, Г.Е.Кузмак – «Оптимальные перелеты космических аппаратов с двигателями большой тяги», Москва «Наука» 1976г.
3). П.Е.Эльязберг – «Введение в теорию полета искусственных спутников земли», Москва 1965г.
4). Р.Ф.Апазов, О.Г. Сытин – «Методы проектирования траекторий носителей и искусственных спутников Земли», Москва «Наука» 1987г.
5). К.А.Абгорян, И.М.Рапопорт – «Динамика ракет», М., Машиностроение 1969г.
|
|
|
6). М.Б.Балк – «Элементы динамики космического полета», М., «Наука» 1965г.
7). А.А.Лебедев, Г.Ф.Герасюта – «Баллистика ракет», М., Машиностроение 1970г.
8. Список сокращений:
ОСК – орбитальная объектоцентрическая система координат.
ЦСК – орбитальная цилиндрическая объектоцентрическая система координат.
ЛА – летательный аппарат.
КА – космический аппарат.
ИСЗ – искусственный спутник Земли.
ЦК – центр координат.
ЦМ – центр масс.
СК – система координат.
ПО – программное обеспечение.
|
|
|
