 |
Частично и общерекурсивные функции.
|
|
|
|
Функция рекурсивна, если есть эффективная процедура для ее вычисления. Процедура эффективна, если она выполняется по механическим правилам.
Рекурсией называется такой способ задания функции, при котором значения определяемой функции для произвольных значений аргументов выражаются известным образом через значения определяемой функции для меньших значений аргументов.
Совокупность числовых функций совпадающая с совокупность. Всех вычислимых функций – совокупность рекурсивных функций.
Функция является обще-рекурсивной, если она определена посредством ряда уравнений некоторого типа.
Затруднение вызвано тем, что просмотр такого выбора уравнений обычно не убеждает нас в том, что эти уравнения “определяют” какую-либо функцию вообще. Когда говорится “функция”, обычно понимается под этим “правило, которое каждому значению (или набору из п значений, если мы имеем функцию n переменных) ставит в соответствие результирующее значение”. Но в общем случае система уравнений не всегда дает определенное значение.
Т.о. вполне допустимой является ситуация, когда для некоторых точек (или даже для всех!!) значение функции не определено – считается что в этих точках сама функция не определена. Это явление весьма характерно. Поэтому, делая предположение, что система уравнений действительно определяет обще-рекурсивную функцию, нужно всегда проявлять осторожность. Мы обычно требуем дополнительного доказательства этого положения, например, в виде индуктивного доказательства того, что для каждого значения аргумента вычисление завершается выдачей единственного значения.
Вследствие этого будем обычно говорить о частично-рекурсивной функции. Когда мы говорим о частично-рекурсивной функции (или, короче, частичной функции) F (x),то понимаем, что может не существовать значения, определенного для некоторого (или даже любого!) значения х. Если F (x)оказывается определенной для всех значений х, то мы называем ее обще-рекурсивной функцией или, короче, общей функцией. Конечно, любая обще-рекурсивная функция также может считаться частично-рекурсивной.
|
|
|
Тезис Черча в узком смысле: Класс рекурсивных функций тождественен классу всюду определенных вычислимых функций.
Тезис Черча в узком смысле Всякая вычислимая функция с аргументами и значениями является частичнорекурсивной.
Тезис Черча-Клини: Все частичные функции вычислимые посредством алгоритма являются частично-рекурсивными.
Частично-рекурсивная функция это класс числовых функций, который строится при помощи следующих операторов, элементарных арифметических функций
Λ(х)=х+1 оператор ствига
O(x1, x2, xN)=0 оператор онулирования
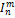=(x1, x2, xN)= xM 1<=m<=n оператор проэктирования
Вопрос 24
В 1936 г Черч сформулировал гипотезу под названием Тезисы Черча.
Тезис Черча в широком смысле:
Класс рекурсивных функций тождественен классу всюду определенных вычислительных функций. (Понятие вычислимой функции точно не определяется поэтому доказать тезис Черча нельзя).
Тезис Черча в узком смысле:
Всякая вычислительная функция с натуральным аргументом и значениями является частично-рекурсивной.
Тезис Черча-Клини:
Все частичные функции, вычисляемые посредством алгоритма, являются частично рекурсивными.
Тезис Черча оказался достаточным, чтобы придать необходимую точность формулировке алгоритмических проблем и в ряде случаев сделать возможным доказательство их неразрешимости.
Вопрос 25
Частично рекурсивные функции – класс числовых функций, который строится при помощи следующих операторов, называемых элементарными арифметическими функциями:
|
|
|
1) 
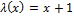– оператор сдвига или функция непосредственного следования.
2) 
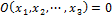– оператор аннулирования или функция тождественно равная 0
3) 
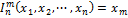– оператор проектирования или функция повторяющая значения своего аргумента.
Все 3 функции являются всюду определенными и интуитивно вычислимыми.
Для получения новых (производных) частично рекурсивных функций используют следующие 3 операции:
1. Суперпозиция функции.
Заключается в подстановке одних арифметических функций вместо аргументов других.
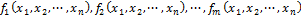
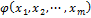тогда ψ, получаемая по правилу
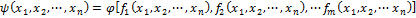, называется функцией полученной в результате суперпозиции 
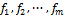и φ.
٭Если 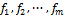и φ всюду определены то и ψ будет всюду определена.
Если хотя бы одна не всюду определена то и ψ будет не всюду определена.
Если необходимо составить суперпозицию функций, имеющих разное число аргументов, то вводят фиктивные аргументы.
2. Схема примитивной рекурсии позволяет строить n-местную арифметическую функцию по двум заданным, одна из которых является n+1-местной, а вторая n-1-местной.
Пусть
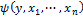– n+1-местная и
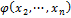– n-1 – местная
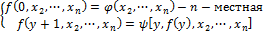
٭ справедливо.
Пример:
Пусть
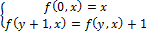
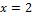
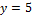
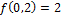
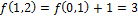
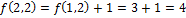
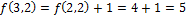
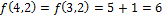
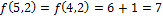(процедура закончена).
Ответ:7.
Функции которые могут быть построены из элементарных арифметических функций с помощью операции суперпозиции и схемы примитивной рекурсии примененных любое количество раз в произвольной последовательности называются примитивно рекурсивными функциями.
Примеры примитивно рекурсивных функций:
1) Функции перестановки аргументов
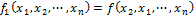
2) Функции циклической перестановки
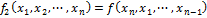
3) Функция отождествления аргумента
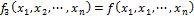
4) Функции фиктивного аргумента
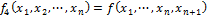
5) 
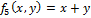
6) 
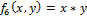
7) 
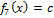
8) 
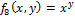
9) 
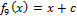
3. Операция наименьшего корня, операция минимизации М-оператор позволяет определять новую арифметическую функцию от n аргументов с помощью ранее построенной от n+1 переменной.
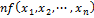
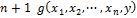
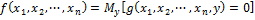
В качестве значения f принимается наименьший целый неотрицательный корень y, при котором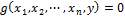 
Процедура вычисления:
1) 
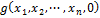if 
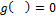then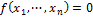 
Else go to next
2) 
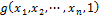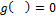if then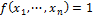 
Else go to next
3) 
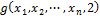
Вычисляется пока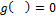
Если не приближается, а отдаляется от 0, то f не определена.
Если 
не определена – процесс прекращается f тоже не определена.
Пример:
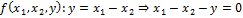
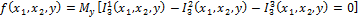
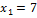
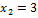
1) 
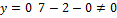
2) 
˖˖˖
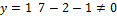
3) 
|
|
|
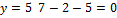
Ответ: f=5
Вопрос 27
Машина Тьюринга - это универсальная учебная машина, созданная для уточнения понятия алгоритм.
Первым из всех ученых идею универсального исполнителя предложил Алан Тьюринг (1936г.). Для уточнения понятия алгоритма, им был разработан абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга.
Структура машины Тьюринга
Машина Тьюринга состоит из:
- бесконечной в обе стороны ленты, разделенной на ячейки;
- каретки (читающей и записывающей головки);
- программируемого автомата.
Программируемый автомат управляет кареткой, посылая ей команды в соответствии с заложенной в него сменяемой программой. Лента выполняет роль внешней памяти компьютера, автомат — роль процессора, а каретка служит для ввода и вывода данных.
|
|
|
