 |
Верхняя и нижняя оценки сложности.
|
|
|
|
Оценки сложности алгоритма.
1) Необходимость получения оценок или границ объема памяти и времени работы, которые могут потребоваться алгоритму.
Узкие места алгоритма – такие части алгоритма, которые требуют очень много времени и памяти.
2) Необходимость выбрать критерии для сравнения алгоритма.
- выработка абсолютного критерия
- выработка для сравнения 2-х алгоритмов. (эти критерии отвечают на вопросы: какой алгоритм лучше и насколько какой можно доработать?)
Поиск хорошо понимаемых оценок сложности включает:
1) верхняя оценка.
они строятся
а) указывается неформально алгоритм вычилсит. функции (расписать по этапам).
б) алгоритм реализуется на подходящей модели
в) доказывается, что сложность алгоритма не превосходит некоторые значения подходящей функции Ф. Функция Ф объявляется верхней оценкой.
2) нижняя оценка – доказать, что никакой алгоритм не имеет сложности вычисления меньше заданной функции Ф.
(если оценка велика, то алгоритм применять не стоит)
Вопрос 45
Предел сложности Бреммермана.
В 1962 г. Бреммерман выдвинул положение:
«Не существует системы обработки данных искусственной или естественной.которая могла бы обрабатывать более. чем 
бит/с на 1 грамм своей массы»
Для работы информация должна быть закодирована. Пример: 0 – напряжение +5 В, 1 – нет напряжения.
Предположим имеется энергия 
, энергетические уровни измеряются точностью 
Тогда общее число энергетических уровней определяется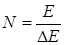 
(1).
Если использовать все энергетич. уровни N, то увеличить общий объём представленной информации можно:
1) Е увеличивают, но здесь мы ограничены энергоносителями в рамках планеты.
2) уменьшают, но уменьшать до бесконечности нельзя т.к мы ограничены соотношением Гейзенберга. 
эрг/сек.
|
|
|
Из соотношений (1) (2) следует 
, 
, m = 1 тр., 
.
тогда 
то есть примерно 
.
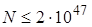Если в это соотношение подставить массу и возраст Земли. (
,m =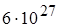 
1 год 
сек. то 
бит – предел Бреммермана
Все задачи.которые требуют обработки информации 
называются трансвычислительными.
Предел Бреммермана при решении задач достигается довольно быстро. Если имеется n переменных принимающ. k значений, то число состояний алгоритмов 
Вопрос 46
Под задачей понимается некоторый вопрос, на который нужно найти (вычислить) ответ. Задачи бывают массовыми (общими) и частными (индивидуальными). Общая задача определяется: • списком параметров – свободных переменных, конкретные значения которых неопределенны; • формулировкой условий – свойств, которыми должен обладать ответ (решение задачи). Массовые задачи часто называют алгоритмическими проблемами. Частная задача получается из массовой, если всем параметрам массовой задачи придать конкретные значения – здесь исходные данные. В общем случаи для любой алгоритмически разрешимой задачи существует несколько разрешающих алгоритмов. С практической точки зрения важно не просто существование разрешающих алгоритмов, а поиск среди них наиболее простого и наименее трудоемкого. Под сложностью задачи принято понимать минимальную из сложностей алгоритмов, решающих эту задачу. Компьютерные науки пока не накопили достаточно сведений для того, чтобы задача минимизации сложности алгоритма была поставлена математически строго. Поэтому без ответов остаются такие вопросы, связанные с нижней оценкой сложности алгоритмов, а значит, и сложности задач: • Существует ли для заданной задачи алгоритм минимальной сложности? • Как убедиться, что найденный алгоритм действительно минимальный или, напротив, не минимальный? • Можно ли для рассматриваемой задачи доказать, что никакой разрешающий ее алгоритм не может быть проще найденной нижней оценки сложности? При разработке алгоритмов можно наблюдать, что для некоторых задач можно построить алгоритм полиномиальной сложности. Такие задачи называют полиномиальными. Полиноминально разрешимые задачи можно успешно решать на компьютере и даже в тех случаях, когда они имеют большую размерность. Для других задач не удается найти полиномиальный алгоритм.поэтому их называют трудноразрешимыми. К классу трудноразрешимых задач относится большое число задач алгебры, математической логики, теории графов, теории автоматов и других разделов дискретной математики. В большинстве своем это так называемые переборные задачи. Переборная задача характеризуется экспоненциальным множеством вариантов, среди которых нужно найти решение, и может быть решена алгоритмом полного перебора. Переборный алгоритм имеет экспоненциальную сложность и может хорошо работать только для небольших размеров задачи. С ростом размера задачи число вариантов быстро растет, и задача становится практически неразрешимой методом перебора. Многие из переборных задач являются экспоненциальными по постановке. Экспоненциальные по постановке задачи не представляют особого интереса для теории алгоритмов, поскольку для них, очевидно, невозможно получить алгоритм полиномиальной сложности. Возникает вопрос: если известно, что некоторая задача алгоритмически разрешима, то неудача в разработке для нее полиномиального разрешающего алгоритма является следствием неумения конкретного разработчика или следствием каких-то свойств самой задачи? Ответ на этот вопрос дает классическая теория алгоритмов, которая классифицирует задачи по сложности. При этом классифицируются лишь распознавательные задачи – задачи, имеющие распознавательную форму. В распознавательной форме суть задачи сводится к распознаванию некоторого свойства, а ее решение – один из двух ответов: «да» или «нет». С точки зрения математической логики задаче распознавания свойства соответствует предикат Р(х), где х – множество фактических значений входных переменных задачи. Существуют задачи, которые изначально имеют распознавательную форму. Например, являются ли два графа изоморфными? Другой пример – задача о выполнимости булевой функции, которая является исторически первой распознавательной задачей, глубоко исследованной в теории алгоритмов. Многие задачи, которые в исходной постановке представлены в иной форме (к ним относятся задачи дискретной оптимизации), довольно просто приводятся к распознавательной форме. Например, если требуется найти хроматическое число графа, то формулируют вопрос: верно ли, что заданный граф является k – раскрашиваемый, где k – заданное целое положительное число. Между тем, имеются задачи, которые нельзя привести к распознавательной форме. Это. В первую очередь, конструктивные задачи – задачи на построение объектов дискретной математики, обладающих заданными свойствами: генерация всех подмножеств конечного множества; генерация всех n! Различных перестановок; построение плоской укладки графа; построение остовного дерева графа и т. п. Такие задачи могут быть как трудноразрешимыми, так и полиноминально разрешимыми. Они пока не попадают под существующую в теории алгоритмов классификацию.
|
|
|
|
|
|
Вопрос 47
Классы сложности
В рамках классической теории осуществляется классификация задач по классам сложности (P-сложные, NP-сложные, экспоненциально сложные и др.). К классу P относятся задачи, которые могут быть решены за время, полиномиально зависящее от объёма исходных данных, с помощью детерминированной вычислительной машины (например, машины Тьюринга), а к классу NP — задачи, которые могут быть решены за полиномиально выраженное время с помощью недетерминированной вычислительной машины, то есть машины, следующее состояние которой не всегда однозначно определяется предыдущими. Работу такой машины можно представить как разветвляющийся на каждой неоднозначности процесс: задача считается решённой, если хотя бы одна ветвь процесса пришла к ответу. Другое определение класса NP: к классу NP относятся задачи, решение которых с помощью дополнительной информации полиномиальной длины, данной нам свыше, мы можем проверить за полиномиальное время. В частности, к классу NP относятся все задачи, решение которых можно проверить за полиномиальное время. Класс P содержится в классе NP. Классическим примером NP-задачи является задача о коммивояжёре.
|
|
|
Поскольку класс P содержится в классе NP, принадлежность той или иной задачи к классу NP зачастую отражает наше текущее представление о способах решения данной задачи и носит неокончательный характер. В общем случае нет оснований полагать, что для той или иной NP-задачи не может быть найдено P-решение. Вопрос о возможной эквивалентности классов P и NP (то есть о возможности нахождения P-решения для любой NP-задачи) считается многими одним из основных вопросов современной теории сложности алгоритмов. Ответ на этот вопрос не найден до сих пор. Сама постановка вопроса об эквивалентности классов P и NP возможна благодаря введению понятия NP-полных задач. NP-полные задачи составляют подмножество NP-задач и отличаются тем свойством, что все NP-задачи могут быть тем или иным способом сведены к ним. Из этого следует, что если для NP-полной задачи будет найдено P-решение, то P-решение будет найдено для всех задач класса NP. Примером NP-полной задачи является задача о конъюнктивной форме
Исследования сложности алгоритмов позволили по-новому взглянуть на решение многих классических математических задач и найти для ряда таких задач (умножение многочленов и матриц, решение линейных систем уравнений и др.) решения, требующие меньше ресурсов, нежели традиционные.
Вопрос 48
|
|
|
