 |
Универсальная машина Тьюринга
|
|
|
|
До сих пор мы придерживались той точки зрения, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако можно построить универсальную машину Тьюринга, способную в известном смысле выполнять любой алгоритм, а значит, способную выполнять работу любой машины Тьюринга.
В универсальной машине Тьюринга, как и во всякой Тьюринговой машине, информация изображается символами, расположенными одновременно на магнитной ленте. При этом универсальная машина Тьюринга может располагать лишь фиксированным конечным внешним алфавитом. Между тем она должна быть приспособлена к приему в качестве исходной информации всевозможных состояний устройства управления и конфигураций, в которых могут встречаться буквы из разнообразных алфавитов со сколь угодно большим числом различных букв.
Это достигается путем кодирования конфигурации и программы любой данной машины Тьюринга в символах входного (внешнего) алфавита универсальной машины. Само кодирование должно выполняться следующим образом:
1) различные буквы должны заменяться различными кодовыми группами, но одна и та же буква должна заменяться всюду, где бы она ни встречалась, одной и той же кодовой группой;
2) строки кодовых записей должны однозначным образом разбиваться на отдельные кодовые группы;
3) должна иметь место возможность распознать, какие кодовые группы соответствуют различным сдвигам, т. е. каждой из букв Л, П, С в отдельности, и различать кодовые гру 2>Таким образом, если какая-либо машина Тьюринга Т решает некоторую задачу, то и универсальная машина Тьюринга способна решить эту задачу при условии, что кроме кодов исходных данных этой задачи на ее ленту будет подан код программы машины Т. Задавая универсальной машине Тьюринга Тu изображение программы любой данной машины Тьюринга Тn и изображение любого ее входного слова xn, получим изображение выходного слова уn, в которое машина Тn переводит слово xn.
|
|
|
Если же алгоритм, реализуемый машиной Тn, не применим к слову xn, то алгоритм, реализуемый универсальной машиной Тu, также не применим к слову, образованному из изображения xn и программы машины Тn.
Таким образом, машина Тьюринга Тn может рассматриваться как одна из программ для универсальной машины Tu.
В связи с существованием универсальной тьюринговой машины таблицы соответствия, описывающие различные состояния устройства управления машины, имеют двоякое назначение:
1) для описания состояний устройства управления специальной машины Тьюринга, реализующей соответствующий алгоритм;
2) для описания программы, подаваемой на ленту универсальной машины Тьюринга, при реализации соответствующего алгоритма.
Современные электронные вычислительные машины строятся как универсальные; в запоминающее устройство наряду с исходными данными поставленной задачи вводится также и программа ее решения.
Вопрос 32
Композиции машин Тьюринга
С математической точки зрения машина Тьюринга — просто определенный алгоритм для переработки слов.
Операции композиции, выполняемые над алгоритмами, позволяют образовы-вать новые, более сложные алгоритмы из ранее известных простых алгоритмов. Поскольку машина Тьюринга—алгоритм, то операции композиции применимы и к машинам Тьюринга. Рассмотрим основные из них, а именно: произведение, возве-дение в степень, итерацию.
Пусть заданы машины Тьюринга Т1 и Т2, имеющие какой-то общий внешний алфавит А = {а0, а1,..., аm} и внутренние алфавиты Q1 = {q0, q1,..., qn} и
cоответственно Q2 = {q0,q1,…,qt}. Композитом, или произведением, машины Т1 на машину T2 будем называть машину Т с тем же внешним алфавитом А= {а0, а1,..., аm}, внутренним алфавитом Q = {q0, q1,...,qn, qn+1,...,qn+t} и программой, получающейся следующим образом. Во всех командах Т1 содержащих заключитель-ный символ q0, заменяем его на символ qn+1. Все остальные символы в командах T1 оставляем неизменными. В командах Т2, напротив, символ q0 оставляем неизменным, но зато каждый из остальных символов заменяем символом qn+j. Совокупность всех команд Т1 и Т2, измененных указанным способом, и будет программой композита или произведения машин T1 и T2.
|
|
|
Произведение машины T1 на машину Т2 обозначается через Т = T1 • T2, или Т = T1 * Т2. Таким образом, машина Т есть произведение машин Т1 и T2, если последовательная работа этих двух машин эквивалентна работе одной машины Т.
Вопрос 33
Поскольку машина Тьюринга - алгоритм, то операции композиции применимы и к машинам Тьюринга. Рассмотрим основные из них: произведение, возведение в степень, итерацию.
Пусть заданы машины Тьюринга T1 и Т2, имеющие общий внешний алфавит A = {a0, a1, …, аm} и внутренние состояния Q1 = {q0, q1,..., qn} и Q2 = {q0, g1,..., qt} соответственно. Композицией или произведением машины T1 и машины Т2 будем называть машину Т с тем же внешним алфавитом A = {a0, a1, …, аm} и набором внутренних состояний Q = {q0, q1, …,qn, qn+1, …, qn+t} и программой, эквивалентной последовательному выполнению программ машин Т1 и Т2:
T = T1 * Т2
Таким же образом определяется операция возведения в степень: n -й степенью машины T называется произведение T... Т с n сомножителями.
Операция итерации применима к одной машине и определяется следующим образом. Пусть машина Т1 имеет несколько заключительных состояний. Выберем ее r -е заключительное состояние и отождествим его в схеме машины с ее начальным состоянием. Полученная машина является результатом итерации машины Т1: T = Т1.
Альтернативное представление машины Тьюринга в виде ориентированных графа, где вершинами являются состояниями, возможные переходы между ними — ребрами, причем начало ребра помечено символом, который должен быть на ленте для активации перехода, а конец ребра помечен символом, который пишется на ленту, и командой перемещения головки («L», «R», «_»):
|
|
|

ПРИМЕР:
Условие:
Для слова babaaa:
а) Построить граф переходов машины Тьюринга
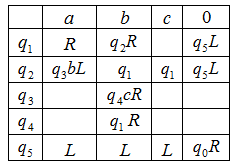
б) Составить протокол работы машины Тьюринга.
Решение:
а) Граф переходов

б) Протокол работы:

Вопрос 34
Понятие вычисления на машине Тьюринга. Вычисление арифметических функций на МТ.
Вычисление арифметических функций на МТ (совок-ть правил) –это понятие вводится для обеспечения единообразного состояния МТ в начале и в конце работы машины, чтобы она могла использоваться в качестве композиции.
МТ вычисляет функцию  . Если каковы бы не были числа
. Если каковы бы не были числа  существует такой момент времени в котором:
существует такой момент времени в котором:
1. МТ достигает заключительного состояния 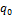 ;
;
2. На ленте будет представлена система из n+1 числа, где  , х- рез-т
, х- рез-т  , который машина воспринимает в стандартном положении.
, который машина воспринимает в стандартном положении.
3. Все ячейки расположенные правее управляющей головки пусты.
Рассмотрим МТ вычисление элементарные арифметические функции:
· Машина обращается к след числу: 
· Для обращения к предыдущему числу: 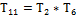
· Машина для функции непосредственного следования: 
· Машина для организации циклов (для конечного числа):  в скобках
в скобках 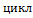
Т-будет пониматься любая машина, которую необходимо зациклить.
· Таблица для перемножения чисел: н-р 011..1011..10 в рез-те получим 011..1011..1011..10
Восновуположентакойалгоритм: S:=0; for i:= 1 to  do; for j:= 1 to
do; for j:= 1 to 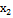 do; S:=S+1;
do; S:=S+1;
mul(вложенность) 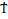 –внешний цикл;
–внешний цикл;  -внутренний цикл;
-внутренний цикл;
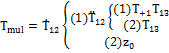 Теорема Тьюринга. Для каждой частично рекурсивной словарной функции
Теорема Тьюринга. Для каждой частично рекурсивной словарной функции  определенной в некотором алфавите
определенной в некотором алфавите  существует МТ с символами
существует МТ с символами 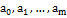
Оценка сложности по отношению к МТ:
МТ используется как критерий для установления разрешимости или не разрешимости проблемы.
Вопрос 35
Нормальные алгоритмы А. А. Маркова. Графическое представление, принцип нормализации, пример.
Алгоритмическая система основана на соответствии между словами в абстрактном алфавите и включает в себя объекты двоякой природы:
1. Элементарные операторы – это достаточно просто задаваемые алфавитные операторы с помощью последовательного выполнения, которых реализуются любые алгоритмы в рассматриваемой алгоритмической системе.
|
|
|
2. Элементарные распознаватели служат для распознавания тех или иных свойств переработки инф., и для изменения в зависимости от рез-тов распознавания последоват., в которой будут выполняться элементарные операторы.
В нормальных алгоритмах Маркова используется единственный оператор – подстановки. Обычно отображают в виде граф-схемы в которой имеются 2 особых узла: вход, выход. Из каждого узла сопоставл. распознавателя выходит = 2 дуги, и с каждого узла сопоставления подстановки = 1 дуга. Кол-во входящих дуг может быть различно. Входное слово поступает на вход. Далее двигаются по стрелкам. Снова попадая в узел распознавателя, проверяет на наличие условия. Если условия выполняются далее двигаются по стрелкам к узле ЭО, в противном случае к след.распознавателю.
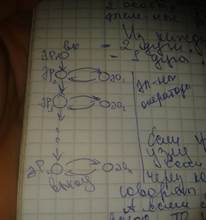
Если входное слово проходя через узлы схемы через конечное число шагов попадает на выход, то алгоритм применим к этому слову. А если слово двигается по схеме бесконечно долго, не попадая на выход, то говорят что алгоритм не применим к этому слову.
 --последовательность слова, которая получается после преобразования данного слова называется дедуктивной цепочкой. Алгоритмы которые задаются графами составлены исключительно из распознавателей вхождения слов и операторов подстановки называют обобщенными норм.алгоритмами.
--последовательность слова, которая получается после преобразования данного слова называется дедуктивной цепочкой. Алгоритмы которые задаются графами составлены исключительно из распознавателей вхождения слов и операторов подстановки называют обобщенными норм.алгоритмами.
Нормальные алгоритмы должны удовлетворять след.условию:
1. Все узлы соответств. распознавателя должны быть упорядочены с помощью их номерации от 1 до n.
2. Дуги, исходящие из узлов подстановки подсоединяются либо к распознователю, либо к выходному узлу.
3. Входной узел подсоединяется к первому распозн..
В качестве пустого символа пишут –e или ƛ. Внутри слова пустой символ не пишется.
Принцип нормализации.
Принцип нормализации любого алгоритма (конструктивно-заданного алфавитного отображения), в произвольном конечном алфавите А можно построить эквивал. ему алгоритм над алгоритмом А.
Принцип нормализации математически доказать не возможно, поскольку здесь используется не строгое матем. использование алгоритма. Справедливость этого принципа позволяет выполнять операции композиции нормальных алгоритмов. В результате такой операции будет получен нормальный алгоритм, который не выходит за пределы класса нормальных алгоритмов.
Пример:

Вопрос 36
композиция нормальных алгоритмов Маркова: суперпозиция, объединение, разветвление и повторение (итерация).
1. При суперпозиии 2-х алгоритмов A и B выходное слово 1-го алгоритма рассматривается как 2-е слово входного алгоритма.
|
|
|

2. Объединение алгоритмов А и В в одном и том же алгоритме называется алгоритм С в том же алфавите преобразует любое входное слово содержащееся в пересечении образовав.определ. А и В в записанные рядом слова А(р)  В(р)
В(р)  В(р)
В(р)  А(р).
А(р).

3. Разветвление алгоритма представляет собой композицию 3-х алгоритмов А, В, С результат D имеет область совпадения с пересечением. Область определения всех 3 алгоритмов A,B, C и для любого входного слова p 

4. Повторение или итерация представляют собой композицию 2-х алгоритмов А и В.
Входное слово получается в результате последовательного многократного применения алгоритма А до тех пор пока не будет получено слово переработанное алгоритмом В, в некоторой фиксированной аналогии цикла с постусловием.

Вопрос 37
Теорема Маркова об универсальном нормальном алгоритме.
Существует такой универсальный нормальный алгоритм, который для любого нормального алгоритма N и для любого входного слова p из области определения алгоритма переводит в слово  , являющееся изображением входного слова
, являющееся изображением входного слова 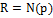 .
.
Из этой теоремы вытекает возможность построения машины, которая может выполнять работу любого нормального алгоритма.
Нормальный алгоритм-это алгоритм который задается графами и составленный исключительно из распознавателей вхождения слов и операторов подстановки.
Вопрос 38
Схема нормального алгоритма Маркова. Теоремы Маркова и Детловса, их значение.
 схема.
схема.
Теорема Маркова.
Существует такой универсальный нормальный алгоритм, который для любого нормального алгоритма N и для любого входного слова p из области определения алгоритма переводит в слово  , являющееся изображением входного слова
, являющееся изображением входного слова 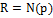 .
.
Из этой теоремы вытекает возможность построения машины, которая может выполнять работу любого нормального алгоритма.
Теорема Детловса.
Класс нормальных вычислительных частичных функций заданных в произвольном алгоритме А совпадает с классом всех одноместных частично рекурсивных словарных функций в алфавите А.
Вопрос 39
Принципы фон Неймана
Использование двоичной системы счисления в вычислительных машинах. Преимущество перед десятичной системой счисления заключается в том, что устройства можно делать достаточно простыми, арифметические и логические операции в двоичной системе счисления также выполняются достаточно просто.
Программное управление ЭВМ. Работа ЭВМ контролируется программой, состоящей из набора команд. Команды выполняются последовательно друг за другом. Созданием машины с хранимой в памяти программой было положено начало тому, что мы сегодня называем программированием.
Память компьютера используется не только для хранения данных, но и программ. При этом и команды программы и данные кодируются в двоичной системе счисления, т.е. их способ записи одинаков. Поэтому в определенных ситуациях над командами можно выполнять те же действия, что и над данными.
Ячейки памяти ЭВМ имеют адреса, которые последовательно пронумерованы. В любой момент можно обратиться к любой ячейке памяти по ее адресу. Этот принцип открыл возможность использовать переменные в программировании.
Возможность условного перехода в процессе выполнения программы. Не смотря на то, что команды выполняются последовательно, в программах можно реализовать возможность перехода к любому участку кода.
Самым главным следствием этих принципов можно назвать то, что теперь программа уже не была постоянной частью машины (как например, у калькулятора). Программу стало возможно легко изменить. А вот аппаратура, конечно же, остается неизменной, и очень простой.
Для сравнения, программа компьютера ENIAC (где не было хранимой в памяти программы) определялась специальными перемычками на панели. Чтобы перепрограммировать машину (установить перемычки по-другому) мог потребоваться далеко не один день. И хотя программы для современных компьютеров могут писаться годы, однако они работают на миллионах компьютеров после несколько минутной установки на жесткий диск.
Как работает машина фон Неймана

Машина фон Неймана состоит из запоминающего устройства (памяти) - ЗУ, арифметико-логического устройства - АЛУ, устройства управления – УУ, а также устройств ввода и вывода.
Программы и данные вводятся в память из устройства ввода через арифметико-логическое устройство. Все команды программы записываются в соседние ячейки памяти, а данные для обработки могут содержаться в произвольных ячейках. У любой программы последняя команда должна быть командой завершения работы.
Команда состоит из указания, какую операцию следует выполнить (из возможных операций на данном «железе») и адресов ячеек памяти, где хранятся данные, над которыми следует выполнить указанную операцию, а также адреса ячейки, куда следует записать результат (если его требуется сохранить в ЗУ).
Арифметико-логическое устройство выполняет указанные командами операции над указанными данными.
Из арифметико-логического устройства результаты выводятся в память или устройство вывода. Принципиальное различие между ЗУ и устройством вывода заключается в том, что в ЗУ данные хранятся в виде, удобном для обработки компьютером, а на устройства вывода (принтер, монитор и др.) поступают так, как удобно человеку.
УУ управляет всеми частями компьютера. От управляющего устройства на другие устройства поступают сигналы «что делать», а от других устройств УУ получает информацию об их состоянии.
Управляющее устройство содержит специальный регистр (ячейку), который называется «счетчик команд». После загрузки программы и данных в память в счетчик команд записывается адрес первой команды программы. УУ считывает из памяти содержимое ячейки памяти, адрес которой находится в счетчике команд, и помещает его в специальное устройство — «Регистр команд». УУ определяет операцию команды, «отмечает» в памяти данные, адреса которых указаны в команде, и контролирует выполнение команды. Операцию выполняет АЛУ или аппаратные средства компьютера.
В результате выполнения любой команды счетчик команд изменяется на единицу и, следовательно, указывает на следующую команду программы. Когда требуется выполнить команду, не следующую по порядку за текущей, а отстоящую от данной на какое-то количество адресов, то специальная команда перехода содержит адрес ячейки, куда требуется передать управление.
Вопрос 40-41
Оценка сложности алгоритмов.
Причины анализа сложности:
1) Необходимость получения оценок или границ объема памяти, которой может потребоваться алгоритму. Выявление «узких» мест алгоритмов по времени или памяти.
2) Необходимость выработать критерии для сравнения алгоритмов:
-выработка абсолютного критерия;
-выработка критерия для сравнения двух алгоритмов.
Три направления критерия алгоритмов:
1) Поиск хорошо понимаемых оценок сложности.
Выделяют верхние и нижние границы. Пример: Верхняя строится так – указывается неформально алгоритм вычисления некоторой функции, потом реализуется на подходящей модели, и доказывается, что сложность вычисления для этого вычисления, и не превосходит значения подходящей функции Ф. Ф и есть верхняя оценка.(Здесь важно измерить размерность исходных данных). Установить нижнюю границу, это значит доказать что никакой алгоритм не имеет сложности меньше заданной Ф.
2) Включение параметров вычислительной модели в качестве аргументов с сложностную функцию.(оценка сложности Шенона для машин Тьюринга).
3) Аксиоматический подход Блюма.
Функция сложности должна удовлетворять 2ум аксиомам:
1. V(i, x)определена тогда и только тогда, когда С(i, x) (С-функция сложности) определена.
2.Множество (<i, x, y>|C(i, х)=y) разрешимо. («|» означает «при условии»).
Теорема о рекурсивной связи различных мер сложности:
Пусть существует С1 и С2(меры сложности) для одной и той же главной функции V(i, x), тогда существует такая D, что для всех номеров i выполняется:
C1(i, x)>=D(C2(i, x)) и V(i, x) определена.
Теорема о ускорении:
Пусть С-мера сложности, R – всюду определённая вычислимая функция, тогда для любого i, существуют такое j, что справедливо неравенство:
С(i, x)<=R(C(j, x))
Оценка сложности производится для целого класса алгоритмов.
Вопрос 42
Единичная проблема состоит в требовании предъявить объект, удовлетворяющий определенным условиям и называемый решением проблемы; решить проблему — значит указать такой объект; если решение существует, т. е. если проблему можно решить, проблема называется решимой.
Массовая проблема представляет собой серию (как правило, бесконечную) единичных проблем и состоит в требовании решить все эти проблемы; понимание того, что же именно считается решением массовой проблемы, нуждается, разумеется, в уточнении.
Задача (массовая проблема) - некоторый общий вопрос, на который должен быть дан ответ.
Как правило задача имеет 1 или несколько параметров. Фиксированное значение параметров образует исходные данные задачи, которые будем называть входом.
Задав вход массовой проблемы, мы образуем индивидуальную задачу. Таким образом массовую проблему можно рассматривать как множество индивидуальных задач.
Массовая проблема характеризуется:
1) Точным описанием допустимых значений параметров (множество допустимых входов).
2) Заданием условий, которым должен удовлетворять ответ.
Пример задачи.
1. Определить наибольший общий делитель чисел X и Y.
Вход: натуральные числа X и Y.
Ответ: максимальное натуральное число Z, такое, что X%Z=0 и Y%Z=0. (Под операцией % понимается остаток от деления).
Для решения каждой задачи требуются определенные вычислительные ресурсы. Величина, которая численно характеризует объем вычислительных ресурсов, минимально необходимых для решения задачи, называется сложностью задачи. Важно, что сложность задачи может зависеть от входа и в общем случае является функцией некоторых характеристик входа.
Неформальное определение алгоритма: алгоритм решения массовой проблемы П - это пошаговая процедура, которая за конечное время решает любую из индивидуальных задач I принадлежащих П.
Алгоритм должен обладать следующими свойствами:
Описание алгоритма конечно, при этом предполагается, что существует объект, понимающий и выполняющий это описание. Такой объект назовем вычислителем.
1) Должны быть четко указаны условия остановки процесса и что следует считать результатом процесса. (Свойство результативности)
2) Алгоритм решения массовой проблемы П должен быть способен решить любую из индивидуальных задач I принадлежащих П, потратив на решение индивидуальной задачи конечное время. (Свойство называется массовостью.)
3) Процесс решения одной и той же индивидуальной задачи протекает одинаково. (Свойство называется детерминированностью.)
Не для каждого алгоритма очевидно, что он приводит в правильному решению поставленной задачи. Если правильность алгоритма не очевидна, то алгоритм нуждается в доказательстве.
Данное выше определение алгоритма достаточно для большинства применений, но не для всех, ибо существуют такие задачи, для которых построение алгоритма невозможно. Если задача поставлена, то удовлетворительными можно считать два результата ее решения: решение проставленной задачи или доказательство того факта, что решение задачи невозможно. Для такого доказательства не годится неформальное определение алгоритма. Не является удовлетворительным и сведение понятия алгоритма до какого-нибудь из известных языков программирования по причине их сложности.
Понятие алгоритма связано: во-первых с массовой проблемой, которую он призван решать, во-вторых с вычислителем, который будет этот алгоритм выполнять. Различные подходы к формализации понятия алгоритма формализуют как понятие задачи, так и понятие вычислителя.
Вопрос 43
Под сложностью некоторой задачи обычно подразумевают сложность алгоритмов, предназначенных для ее решения и реализуемых в виде вычислительных процедур на компьютерах. Понятие сложности алгоритма чаще всего на интуитивном уровне ассоциируется с его трудоемкостью, т.е. количеством некоторых условных операций, необходимых для завершения работы алгоритма, решающего задачу.
Различают меры сложности алгоритмов двух видов:
· статическая сложность, не зависящая от входных данных задачи;
· динамическая сложность, зависящая от входных данных задачи.
Типичным примером статической меры сложности алгоритма является длинна программы, определяемая, например, количеством операторов языка программирования, использованных для кодирования конкретной реализации алгоритма.
Динамическая мера сложности дает информацию о потребностях алгоритма в ресурсах компьютера как функции входных данных задачи. Типичной динамической мерой сложности являются время вычислений или объем памяти, необходимый для реализации вычислений.
Следует заметить, что различные меры сложности используются в зависимости от условий применения. К тому же в реальных реализациях алгоритмов оценка времени вычислений и объема памяти, необходимой для реализации алгоритма, как правило, не зависимы: сокращение одной из них достигается не редко за счет возрастания другой.
Временная сложность обычно является наиболее важным фактором, ограничивающим размеры задач, которые могут быть решены на современных вычислительных машинах.
Временная сложность - это функция, отображающая параметры задачи на время, требуемое для решения задачи. Применительно к этой мере сложности рассматривают задачи по определению нижних и верхних границ сложности, оценок сложности в среднем, асимптотических оценок сложности, сложности модели вычислений и способа представления задачи.
Для многих алгоритмов неизвестно точных верхних и/или нижних оценок. Поэтому оказывается удобным при анализе алгоритмов подсчитывать только количество "элементарных" операций, а о сложности алгоритмов судить по асимптотическому росту числа элементарных операций.
В теории сложности выделяют два фундаментальных класса алгоритмов:
· алгоритмы, сложность которых оценивается полиномом от размерности задачи;
· алгоритмы с экспоненциальной оценкой сложности.
Зависимость времени вычислений для алгоритмов экспоненциальной сложности от параметров (размерности задачи) является существенно более сложной.
Сравнение алгоритмов можно производить по вычислительным оценкам сложности. Некоторые алгоритмы обладают полиномиальной сложностью, другие экспоненциальной сложностью. В то же время ряд алгоритмов занимают занимают некоторое промежуточное положение. Полиномиальных алгоритмов для таких задач не предложено, но и не доказано, что их не может быть.
Формальным изучением отмеченного феномена, занимается теория NP-полных задач. Класс NP-полных задач обладает следующими свойствами:
1. Никакую NP-полную задачу нельзя решить никаким известным алгоритмом полиномиальной сложности;
2. Если будет найден полиномиальный алгоритм для какой-нибудь NP-полной задачи, то существуют полиномиальные алгоритмы для всех NP-полных задач.
Основываясь на этих двух фактах, многие исследователи высказывают гипотезу, что ни для какой NP-полной задачи не может существовать полиномиального алгоритма. Однако некому пока не удалось доказать это.
Практическое значение классификации некоторой задачи как NP-полной задачи заключается в том, если задача отнесена к NP-полной, то она по существу труднорешаема с вычислительной точки зрения. Эффективные (полиномиальные) алгоритмы для данной задачи целесообразно искать на некоторых более узких множеств входных параметров задачи.
Таким образом, исследователь, который сталкивается с новой комбинаторной задачей оптимизации и не может найти для нее эффективного алгоритма, может попытаться доказать, что задача NP-полна. Если о задаче станет известно, что она NP-полна, то обычно дальнейшее ее изучение исходит из менее амбициозных целей, чем построение алгоритма, который всегда находит точное (оптимальное) решение и время работы которого никогда не превышает некоторой полиномиальной оценки.
При решении задачи - расчета рабочих графиков для многосменного режима работы исследователи, как правило, в первую очередь обращают свое внимание на, так называемую - общую задачу теории расписаний. Однако, известно, что общая задача теории расписаний является NP-полной.
Вопрос 44
|
|
|


