 |
Неразрешимые задачи и проблемы Теории алгоритмов.
|
|
|
|
Эшби доказал.что вся информация использ. мировой наукой не превышает 
бит. Задача, которая даже если и укладывается в предел Бреммермана может оказаться нерешаемой. Задача считается неразрешимой, если не существует решения на МТ.
Виды неразрешимых задач.
1) Задачи относительно которых не доказано.что они неразрешимы. но алгоритмы их решения не найдены.
2) Остальные задачи.которые в прицепи разрешимы. но их решить нельзя из-за ограничения времени их решения и испрольз. объёмов памяти.
Разрешимость зависит от 3-х факторов:
1) От алгоритма решения
2) От конкретной алгоритмич. системы
3) от мощности ЭВМ
7 неразрешимых проблем:
1) Проблема распознавания истинности формул в элемент.арифметике – проблема требования найти алгоритм. который по всякой формуле определял бы истина она в натур. ряду или нет. Невозможность такого алгоритма следует из перечисл. множества натуральных чисел.
2) Проблема разрешения для логики предикатов I-ого порядка (1936г.) – вытекает из особенности предиката (вход данные бесконечны, а вых. только 0 и 1)
3) Проблема разрешимости Поста – Пусть дано конечное множество пар в некотор. алфавите (сочетаемом).Если для рассмат. пар 
… 
выполняется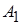 
, 
… 
= 
, 
… 
. Проблема разрешима если алфавит однобуквенный.
4) Проблема эквивалентности слов для ассоциативного исчисления – сформулировал Туэ: «Пусть дано 2 кортежа A и B. Найти алгоритм позволяющий из исчислимого числа операций всегда решать будит ли эвивал. 2 произвольных ряда знаков)»
Требуется построить алгоритм распознающий по вской паре В-слов эквивалентны ли слова в данном вычислении или нет.
5) Проблема представимости матриц. – матр. И представима через матр. 
если для некотор. индексов выполняется равенство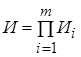 
|
|
|
Общая проблема представимости состоит в требовании указать алгоритм по средствам которого можно было бы узнавать для любой системы матриц { } представима ли И через … Марков доказал что проблема неразрешима для матриц размерности 
6) 10-я проблема Гильберта -Задачи разрешимости диофантовогоур-ия 
7) Проблема тождества элементарных функций вещественных переменных. Проблема указать алгоритм узнающий по 2-ум термам задают ли они одну и тужу функцию веществен.переменного
Вопрос 49
В теории алгоритмов NP-полная задача — задача из класса NP, к которой можно свести любую другую задачу из класса NP за полиномиальное время. Таким образом, NP-полные задачи образуют в некотором смысле подмножество «самых сложных» задач в классе NP; и если длякакой-то из них будет найден «быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
Формальное определение
Алфавитом называется всякое конечное множествосимволов (например,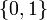 
или 
). Множество всех возможных слов (конечных строк, составленных из символов этого алфавита) над некоторым алфавитом 
обозначается 
. Языком 
над алфавитом называется всякое подмножество множества , то есть 
.
Задачей распознавания для языка называется определение того, принадлежит ли данное слово языку .
Язык 
называется сводимым (по Карпу) к языку 
, если существует функция, 
, вычислимая за полиномиальное время, обладающая следующим свойством:
тогда и только тогда, когда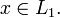 
Сводимость по Карпу обозначается как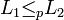 
или 
.
Язык называется NP-трудным, если любой язык из класса NP сводится к нему. Язык называют NP-полным, если он NP-труден, и при этом сам лежит в классе NP.
Таким образом, если будет найден алгоритм, решающий некоторую (любую) NP-полную задачу за полиномиальное время, то все NP-задачи окажутся в классе P, то есть будут решаться за полиномиальное время.
|
|
|
|
|
|
