Плоская сходящаяся система сил. Сложение сил и условие равновесия.

Любое несвободное тело можно сделать свободным, если связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.

Сила, с которой данная связь действует на тело, препятствуя тем ила иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.

Так у тела, лежащего на столе, связь – стол. Тело несвободное. Сделаем его свободным – стол уберем, а чтобы тело осталось в равнове­сии, заменим стол силой, направленной вверх и равной, конечно, весу тела.

Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь одновременно препятствует перемещениям тела по нескольким направлениям, направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.

Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим силам.

Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровые нагрузки и т.п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.

Одна из главных задач статики твердого тела - нахождение реакции связей. Для определения реакции связей необходимо найти величину этой реакции, линию и направление ее действия. Линия действия реакции обычно проходит через точку касания тела и связи. Численное значение реакции определяется расчетом, а направление реакции зависит от вида (конструкции) связи.

Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.

Рассмотрим, как направлены реакции некоторых основных видов связей.

1. Гладкая плоскость (поверхность) или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпен­дикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис.14, а). Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям сопри­касающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис. 14, б), то реакция направлена по нормали к другой поверх­ности.

Если поверхности не гладкие, надо добавить еще одну силу – силу трения , которая направлена перпендикулярно нормальной реакции в сторону, противоположную возможному скольжению тела.

 

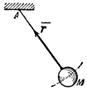
Рис.14 Рис.15

 

Рис.16

2. Нить (гибкие связи). Связь, осуществленная в виде гибкой нерастяжимой нити (рис.15), не дает телу М удаляться от точки подвеса нити по направлению AM. Поэтому реакция Т натянутой нити направлена вдоль нити от тела к точке ее подвеса. Если даже заранее можно догадаться, что реакция направлена к телу, все равно ее надо направить от тела. Таково правило. Оно избавляет от лишних и ненужных предположений и, как убедимся далее, помогает установить сжат стержень или растянут.

3. Цилиндрический шарнир (подшипник). Если два тела соединены болтом, проходящим через отверстия в этих телах, то такое соединение называется шарнирным или просто шарниром; осевая линия болта называется осью шарнира. Тело АВ, прикреплен­ное шарниром к опоре D (рис.16, а), может поворачиваться как угодно вокруг оси шарнира (в плоскости чертежа); при этом конец А тела не может переместиться ни по какому направлению, перпен­дикулярному к оси шарнира. Поэтому реакция R цилиндрического шарнира может иметь любое направление в плоскости, перпен­дикулярной к оси шарнира, т.е. в плоскости А _ху. Для силы R в этом случае наперед не известны ни ее модуль R, ни направле­ние (угол ).

4. Шаровой шарнир и подпятник. Этот вид связи закреп­ляет какую-нибудь точку тела так, что она не может совершать никаких перемещений в пространстве. При­мерами таких связей служат шаровая пята, с помощью которой прикрепляется фото­аппарат к штативу (рис.16, б) и подшипник с упором (подпятник) (рис. 16, в). Реакция R шарового шарнира или подпятника может иметь любое направление в пространстве. Для нее наперед неизвестны ни модуль реакции R, ни углы, образуемые ею с осями х, у, z.

 

Рис.17

5. Стержень. Пусть в какой-нибудь конструкции связью является стержень АВ, закрепленный на концах шарнирами (рис.17). Примем, что весом стержня по сравнению с воспринимаемой им нагрузкой можно пре­небречь. Тогда на стержень будут действовать только две силы при­ложенные в шарнирах А и В. Но если стержень АВ находится в равновесии, то по аксиоме 1 приложенные в точках А и В силы должны быть направлены вдоль одной прямой, т. е. вдоль оси стержня. Следовательно, нагруженный на концах стержень, весом ко­торого по сравнению с этими нагрузками можно пренебречь, работает только на растяжение или на сжатие. Если такой стержень является связью, то реакция стержня будет направлена вдоль оси стержня.

6. Подвижная шарнирная опора (рис.17.1). Это устройство представляет собой опорный элемент (подшипник), внутри которого вращается палец (ось) шарнира. Такая опора не препятствует вращению вокруг оси, но препятствует движению тела в любом направлении в плоскости, перпендикулярной к оси шарнира. Реакция 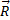такой опоры направлена по нормали к поверхности, на которую опираются катки подвижной опоры. На схемах эту связь изображают так, как показано на рис. 17.1.

 

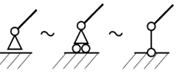
Рис.17.1. Шарнирно подвижная опора:

а – вид катковой опоры; б – расчетная схема шарнирно-подвижных опор

7. Неподвижная шарнирная опора (рис.18). Реакция R шарнирно-неподвижной опоры расположена в плоскости, перпендикулярной оси возможного вращения, и ее направление определяют две взаимно перпендикулярные составляющие R_x и R_y, соответствующие направлению выбранных осей (рис. 18, а). В строительной механике шарнирно-неподвижную опору изображают в виде двух шарнирных стержней пересекающихся в точке опоры (рис.18, б) или шарнира (рис 18, в). При решении задач будем реакцию изображать ее составляющими и по направлениям осей координат. Если мы, решив задачу, найдем и , то тем самым будет определена и реакция ; по модулю R .

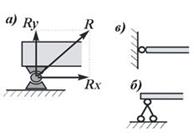
Рис.18. Шарнирно-неподвижная опора:

а – вид шарнирно-неподвижной опоры;

б, в – расчетные схемы шарнирно-неподвижных опор

Способ закрепления, показанный на рис.18, употребляется для того, чтобы в балке не возникало дополнительных напряжений при изменении ее длины от изменения температуры или от изгиба.

8. Неподвижная защемляющая опора или жесткая заделка (рис.19, а). Это соединение исключает возможность каких-либо перемещений абсолютного твердого тела. Балка, изображенная на рис.19, а, жестко заделана в стену в точке А. Перемещению ее в вертикальном направлении, препятствует реакция R_y, перемещению в горизонтальном направлении препятствует реакция R_x и повороту вокруг точки А - опорный момент М_А. Характерным для данной опоры является наличие опорного момента сил, исключающего вращение тела вокруг любой оси. Схематическое изображение такой опоры в теоретической механике показано на рис. 1.9, б. Если под такую балку где-нибудь в точке В подвести еще одну опору, то балка станет статически неопределимой.

С помощью указанных опорных связей сооружения прикрепляются к фундаментам или отдельные элементы соединяются между собой.

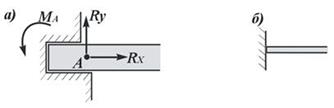
Рис. 19. Жесткая заделка:

а – вид жесткой заделки; б – расчетная схема жесткой заделки

При определении реакций связи других конструкций надо установить, разре­шает ли она двигаться вдоль трех взаимно перпендикулярных осей и вращаться вокруг этих осей. Если препятствует какому-либо движению – показать соот­ветствующую силу, если препятствует вращению – пару с соответствующим моментом.

Иногда приходится исследовать равновесие нетвердых тел. При этом будем пользоваться предположением, что если это нетвердое тело находится в равновесии под действием сил, то его можно рассматривать как твердое тело, используя все правила и методы статики.

Связи, как и другие понятия, встречающиеся в аксиомах, являются абстракциями, весьма условно отражающими свойства реальных объектов. Например, рассмотренная выше гибкая невесомая нить может быть моделью подвесных и вантовых систем, у которых масса погонного метра троса составляет десятки и сотни килограммов. Однако усилия, возникающие в таких тросах, во столько раз больше их собственного веса, что при расчете последним можно пренебречь, считая их невесомым

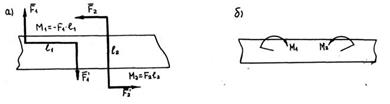
4. Система двух параллельных сил, равных по модулю и направлен­ных в противоположные стороны, называется парой сил или просто парой. Понятие о паре сил ввел в механику французский ученый Луи Пуансо (1777-1859).

Пара сил - неуравновешенная система и не имеет равнодейству­ющей. Пара сил производит на тело вращательное действие.

Вращательный эффект пары измеряется взятым со знаком плюс или минус произведением модуля одной из сил пары на ее плечо (момент пары), т.е.

Знак «плюс» ставится перед числовым значением момента в том случае, если пара стремится повернуть тело против хода часовой стрелки, и знак «минус» если пара стремится повернуть тело по хо­ду часовой стрелки.

В Международной системе единиц (СИ) моменты пар выражаются в или .

Вращательное действие расположенной в данной плоскости пары зависит только от ее момента, поэтому для задания пары сил до­статочно указать числовое значение ее момента, а затем по данно­му или выбранному плечу можно определить силы пары или по силам подобрать необходимое плечо. Исходя из этого, на рисунках и схе­мах пары сил изображают иногда просто круговой стрелкой, харак­теризующей лишь направление вращающего действия. Например, пары () и (), приложенные к брусу, можно условно изобразить круговыми стрелками, обозначив их и .

 

 

5.

 

6. Система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке, называется плоской системой схо­дящихся сил. Если силы сходящейся системы приложены к разным точкам тела, то, по первому следствию из аксиом статики, каждую силу можно перенести в точку пересечения линий действия и по­лучить эквивалентную систему сил, приложенных к одной точке.

Две силы, приложенные к одной точке тела, образуют простей­шую плоскую систему сходящихся сил (две пересекающиеся прямые всегда лежат в одной плоскости).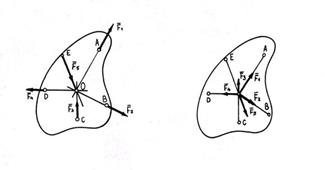

Рассмотрим систему сил , приложенных в точке А. Требуется найти их равнодействующую.Применив правило силового треугольника, сложим силы и . Для этого из конца вектора отложим вектор и, соединив точки А и С, получим геометрическую сумму (равнодейст­вующую) сил и :

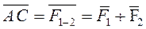
Теперь сложим силу с силой . Для этого из конца вектора ВС= отложим вектор и, соединив точки А и D, по­лучим равнодействующую трех сил:

где — искомая равнодействующая

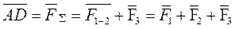
Порядок построения сторон силового многоугольника не влияет на окончательный результат.

Чтобы уравновесить систему сил, достаточно к ней добавить еще одну силу, численно равную равнодействующей, но направленную в противоположную сторону.

.

В геометрической форме необходимое и достаточное условие рав­новесия системы сходящихся сил: система сходящихся сил уравнове­шена тогда и только тогда, когда силовой многоугольник замкнут.

Определение равнодействующей системы

сходящихся сил методом проекций.

Аналитическое условие равновесия.

Вместо построения силового многоугольника равнодействующую

системы сходящихся сил более точно и значительно быстрее находят вычислением с помощью метода проекций, который обычно называется аналитическим.

Проекцией вектора на ось называется длина направленного отрезка оси, заключенного между двумя перпендикулярами, опущен­ными из начала и конца вектора . Проекция силы на ось равна произведению модуля этой силы на косинус угла между направлением силы и положительным направлением оси;

Рассмотрим теперь определение равнодействующей системы сходя­щихся сил методом проекций.

Допустим, что для заданной системы сходящихся сил построен многоугольник ABCDE., в котором вектор

- искомая равно­действующая данной системы.

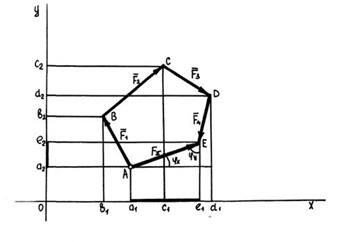
Выбрав систему координатных осей X и Y в плоскости силового многоугольника, спроецируем его на эти оси.

Эти равенства короче записываются так:

,

где - знак суммы, а индекс к принимает последовательно зна­чения от 1 до n по числу сходящихся сил, равнодействующую кото­рых определяем.

Таким образом, проекция равнодействующей системы сходящихся сил на каждую из осей координат равна алгебраической сумме про­екций составляющих сил на ту же ось.

и .

 

В аналитической форме условие равновесия плоской системы схо­дящихся сил: для равновесия плоской системы сходящихся сил необ­ходимо и достаточно, чтобы алгебраические суммы проекций всех сил системы на каждую из двух осей координат были равны нулю

Плоская сходящаяся система сил. Сложение сил и условие равновесия.

ПЛССС - называется система сил, линия действий которых лежат в одной плоскости и пересекаются в одной плоскости.

По следствию из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными в одной точке.

Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома статики).

Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
Вектор равнодействующей силы соединит начало первого вектора с концом последнего.

Для равновесия плоской системы сходящихся сил необходимо, чтобы
равнодействующая этих сил равнялась нулю. Исходя из этого, получим:

Плоская система сходящихся мил находится в равновесии, если
алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

7. П роецирование силы на ось и на плоскость

Проекцией силы F на ось Ox называется скалярная величина F_x, равная произведению ее модуля F на косинус угла между силой и положительным направлением оси:

F_x=F·cos .

Проекция силы на ось:

· положительна, если угол -острый;

· равна нулю, если угол - прямой (сила перпендикулярна оси);

· отрицательна, если угол - тупой.

 

Проекцией силы F на плоскость Oxy называется вектор F _xy, заключенный между проекциями начала и конца силы F на эту плоскость.

В отличие от проекции силы на ось, проекция силы на плоскость является векторной величиной и характеризуется не только числовым значением, но и направлением в плоскости Oxy.

По модулю F_xy=F·cos ,
где - угол между векторами F и F _xy.

Проекция силы на плоскость используется, например, для нахождения проекций силы на оси, лежащие в этой плоскости (см. рис.): F_x=F_xy·cos 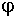; F_y=F_xy·sin .

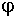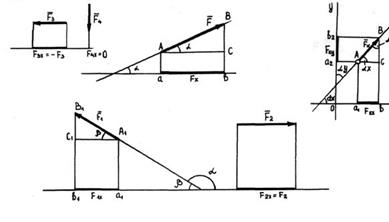
Проекция силы на ось

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 1.15).

рис. 1.15

Величина проекции силы на ось равна произведению модуля си­лы на косинус угла между вектором силы и положительным напра­влением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 1.16).

рис. 1.16

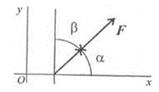
F_1x = F₁ cos α₁ > 0; F_2x = F₂ cos α₂ = - F₂ cos β₂;

cos α₂ = cos (180° - β₂) = - cos β₂;

F_3x = F₃ cos 90° = 0; F_4x = F₄ cos 180° = - F₄

Проекция силы на две взаимно перпендикулярные оси

(рис. 1.17).

F_x = F cos a > 0;

F_y = F cos β = F sin α > 0. рис.1.17

1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: