Произвольная плоская система сил

Если все силы, действующие на твердое тело, лежат на одной плоскости, выберем систему координат xOy в плоскости действия сил (рисунок 2.1). В этом случае обнаружим, что

 

 

Далее, вспомнив определение момента силы относительно оси, замечаем, что сумма моментов всех сил относительно оси z равна алгебраической сумме моментов этих сил относительно начала координат, т.е. точки О.

В результате останутся следующие три аналитические условия равновесия:

 

 

 

Рисунок 2.1

 

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей x и y и сумма моментов всех сил относительно любой точки, лежащих в плоскости действия сил, были равны нулю.

Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.

 

Главным вектором системы сил называется вектор, равный векторной сумме этих сил:

R = ΣF_k. (1.1)

 

Главным моментом системы сил относительно точки O тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки:

M_o = ΣM_o(F_k). (1.2)

Формы условий равновесия произвольной плоской системы сил

· Первая форма условий равновесия

Для равновесия произвольной плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор R этих сил и их главный момент M_o относительно произвольной точки O, лежащей в плоскости действия этих сил, были равны нулю, т.е.

ΣF_k = 0, ΣM_o(F_k) = 0 (1.3)

В координатной форме эти условия выражаются следующими тремя уравнениями:

ΣF_kx = 0, ΣF_ky = 0, ΣM_o(F_k) = 0. (1.4)

Уравнения (1.4) носят название первой формы условий равновесия для произвольной плоской системы сил.

Равновесие плоских систем сил, расположенных произвольно на плоскости, можно выразить еще в двух других эквивалентных формах необходимых и достаточных условий равновесия.

· Вторая форма условий равновесия (теорема о трех моментах)

 

Теорема о трех моментах – алгебраическая сумма моментов сил относительно трех произвольных точек A,B,C, не лежащих на одной прямой, равна нулю, т.е.

 

ΣM_A(F_k) = 0, ΣM_B(F_k) = 0, ΣM_C(F_k) = 0; (1.5)

 

Необходимость этих условий очевидна, т.к. если плоская система сил находится в равновесии, то выполняется первая форма условий равновесия (1.4).

А тогда из последнего равенства (1.4) следует, что сумма моментов всех сил относительно любой точки, следовательно, и точек А, В, С равняется нулю, т.е. выполняются условия (1.5).

 

Достаточность условий (1.5) следует из того, что если выполняются условия (1.5), а данная система сил не находится в равновесии, то она должна была бы приводиться к равнодействующей, одновременно проходящей через точки А, В, С.

 

Это невозможно, т.к. точки А, В, С не лежат на одной прямой. Следовательно, если выполняются условия (1.5), то имеет место равновесие.

Третья форма условий равновесия – алгебраическая сумма моментов всех сил относительно двух любых точек A и B равна нулю и сумма проекций этих сил на ось Ox, не перпендикулярную к прямой, проходящей через точки A и B, равна нулю, т.е.

 

ΣM_A(F_k) = 0, ΣM_B(F_k) = 0, ΣF_kx = 0. (1.6)

 

Необходимость этих условий, так же как и в предыдущем случае, следует из первой формы условий равновесия. Докажем их достаточность, т.е. докажем, что если выполняются условия (1.6), то рассматриваемая система находится в равновесии.

Выполнение первых двух условий (1.6) означает, что главный момент данной системы сил относительно центров приведения А и В равен нулю. Такая система может иметь равнодействующую, приложенную в центре приведения, и при R*¹0 линия действия равнодействующей проходит через точки А и В (рисунок 2.2).

 

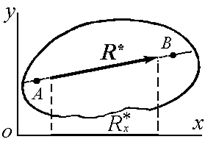Рисунок 2.2

 

Но по третьему условию из (1.6) проекция равнодействующей на ось Оx равна нулю. Так как ось Оx (рис.2) не перпендикулярна АВ, то это последнее условие может быть выполнено только в случае, если R*=0, т.е. когда рассматриваемая система сил уравновешена.

 

В частном случае, если линии действия всех сил плоской системы параллельны (плоская система параллельных сил), то условия равновесия таких сил выражаются не тремя, а двумя уравнениями:

ΣF_kx = 0, ΣM_o(F_k) = 0, (1.7)

причем ось Ox параллельна данным силам, или

 

ΣM_A(F_k) = 0, ΣM_B(F_k) = 0, (1.8)

причем прямая AB не параллельна данным силам.

10. Условия равновесия произвольной плоской системы сил.

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M ₀ = 0.

Здесь О - любая точка плоскости.

Из этого условия следуют уравнения равновесия произвольной плоской системы сил, которые можно записать в трех различных формах:

1) Первая форма:

Σ M_A = 0;

Σ X = 0;

Σ Y = 0.

2) Вторая форма:

Σ M_A = 0;

Σ M_B = 0;

Σ Y = 0, где ось Oy неперпендикулярна отрезку АВ.

3) Третья форма:

Σ M_A = 0;

Σ M_B = 0;

Σ M_С = 0, где точки А, В и С не лежат на одной прямой.

Равенства выражают, следующие аналитические условия рав­новесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каж­дую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.

.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: